推荐系统评价指标及代码实现
评价指标
| 指标 | 意义 | 计算方法 |
|---|---|---|
| 用户满意度 | 最重要的指标 | 用户调查或在线实验,如问卷、“满意”按钮、点击率、停留时间、转化率等 |
| 预测准确度 | 最重要的系统离线指标 | 根据离线用户行为数据集进行评测,如评分预测使用均方根误差(RMSE)或平均绝对误差(MAE)、TopN推荐使用准确率(Precision)/召回率(recall) |
| 覆盖率 | 对物品长尾的发掘能力 | 定义不同,如推荐出的物品占总物品的比例、信息熵、基尼指数 |
| 多样性 | 物品两两之间的不相似性 | 根据相似度定义,如内容相似度、协同过滤相似度 |
| 新颖性 | 从没见过的推荐 | 最简单方法是过滤掉有过行为的物品,或是流行度低的物品 |
| 惊喜度 | 从没见过但令人满意的推荐 | 目前无公认定义 |
| 信任度 | 增加与推荐系统的交互 | 问卷调查 |
离线优化目标:最大化预测准确度,使覆盖率>A,多样性>B,新颖性>C
公式及代码
1. 用户满意度
采用用户调查或在线实验,如问卷、“满意”按钮、点击率、停留时间、转化率等。
2. 预测准确度
评分预测
用户 u u u,物品 i i i, r u i r_{ui} rui为实际评分, r u i ′ r_{ui}^{'} rui′为预测评分
均方根误差
RMSE = ∑ u , i ∈ T ( r u i − r u i ′ ) 2 ∣ T ∣ \text{RMSE}=\sqrt{\frac{\sum_{u,i\in T}{\left( r_{ui}-r_{ui}^{'} \right) ^2}}{|T|}} RMSE=∣T∣∑u,i∈T(rui−rui′)2
平均绝对误差
MAE = ∑ u , i ∈ T ∣ r u i − r u i ′ ∣ T \text{MAE}=\frac{\sum_{u,i\in T}{|r_{ui}-r_{ui}^{'}|}}{T} MAE=T∑u,i∈T∣rui−rui′∣
均方根误差(RMSE)对系统评测更苛刻,越小越好。
import math
def RMSE(records):
'''均方根误差'''
return math.sqrt(sum([(rui - pui) * (rui - pui) for u, i, rui, pui in records]) / len(records))
def MAE(records):
'''平均绝对误差'''
return sum([abs(rui - pui) for u, i, rui, pui in records]) / len(records)
if __name__ == '__main__':
user = ['a', 'b', 'c']
item = ['Python深度学习', '疯狂Java讲义', 'C++ Primer']
records = [['a', 'Python深度学习', 4.3, 5], ['a', '疯狂Java讲义', 4.7, 5], ['a', 'C++ Primer', 4.1, 5],
['b', 'Python深度学习', 4.0, 5], ['b', '疯狂Java讲义', 3.8, 5], ['b', 'C++ Primer', 4.2, 5],
['c', 'Python深度学习', 4.1, 5], ['c', '疯狂Java讲义', 3.0, 5], ['c', 'C++ Primer', 4.9, 5], ]
print(RMSE(records)) # 1.015983376941878
print(MAE(records)) # 0.8777777777777778
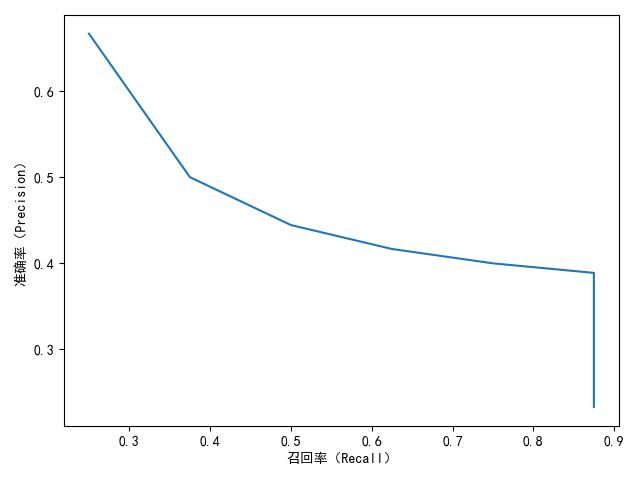
TopN推荐
TopN推荐更符合实际应用,一般通过准确率/召回率曲线
推荐列表 R ( u ) R(u) R(u),行为列表 T ( u ) T(u) T(u)
召回率
Recall = ∑ u ∈ U ∣ R ( u ) ∩ T ( u ) ∣ ∑ u ∈ U ∣ T ( u ) ∣ \text{Recall}=\frac{\sum_{\text{u}\in \text{U}}{|R\left( u \right) \cap T\left( u \right) |}}{\sum_{u\in U}{|T\left( u \right) |}} Recall=∑u∈U∣T(u)∣∑u∈U∣R(u)∩T(u)∣
准确率
Precision = ∑ u ∈ U ∣ R ( u ) ∩ T ( u ) ∣ ∑ u ∈ U ∣ R ( u ) ∣ \text{Precision}=\frac{\sum_{\text{u}\in \text{U}}{|R\left( u \right) \cap T\left( u \right) |}}{\sum_{u\in U}{|\text{R}\left( u \right) |}} Precision=∑u∈U∣R(u)∣∑u∈U∣R(u)∩T(u)∣
from matplotlib import pyplot as plt
def Recommend(user, N=10):
'''推荐算法'''
return ['Python深度学习', '疯狂Java讲义', 'C++ Primer',
'数学之美', '利用Python进行数据分析', '浪潮之巅',
'鸟哥的Linux私房菜', '机器学习', '高性能MySQL', '统计学习方法'][:N]
def PrecisionRecall(records, N=10):
'''准确率和召回率'''
hit = 0
precision = 0
recall = 0
for user, items in records.items():
rank = Recommend(user, N)
hit += len(list(set(rank).intersection(set(items))))
precision += N
recall += len(items)
return [hit / precision, hit / recall]
if __name__ == '__main__':
records = {'a': ['Python深度学习', '疯狂Java讲义', 'C++ Primer'],
'b': ['Python深度学习', '数学之美'],
'c': ['利用Python进行数据分析', '浪潮之巅', 'C++ 机器学习'],
}
x = []
y = []
for N in range(1, 11):
Precision, Recall = PrecisionRecall(records, N)
x.append(Recall)
y.append(Precision)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.xlabel("召回率(Recall)")
plt.ylabel("准确率(Precision)")
plt.plot(x, y)
plt.show()
3. 覆盖率
推荐出的物品占总物品的比例
用户集合 U U U,给每个用户推荐长度为 N N N的列表 R ( u ) R(u) R(u)
Coverage = ∣ ⋃ u ∈ U R ( u ) ∣ ∣ I ∣ \text{Coverage}=\frac{|\bigcup_{\text{u}\in \text{U}}{R\left( u \right)}|}{|I|} Coverage=∣I∣∣⋃u∈UR(u)∣
I = ['Python深度学习', '疯狂Java讲义', 'C++ Primer',
'数学之美', '利用Python进行数据分析', '浪潮之巅',
'鸟哥的Linux私房菜', '机器学习', '高性能MySQL', '统计学习方法']
def Coverage(records):
'''覆盖率'''
total = []
for user, items in records.items():
total += items
return len(total) / len(I)
if __name__ == '__main__':
records = {'a': ['Python深度学习', '疯狂Java讲义', 'C++ Primer'],
'b': ['Python深度学习', '数学之美'],
'c': ['利用Python进行数据分析', '浪潮之巅', 'C++ 机器学习'],
}
print(Coverage(records)) # 0.8
信息熵
H = − ∑ i = 1 n p ( i ) log p ( i ) H=-\sum_{i=1}^n{p\left( i \right) \log\text{\ }p\left( i \right)} H=−i=1∑np(i)log p(i)
基尼指数
i j i_{j} ij是按物品流行度 p p p从小到大排序的第 j j j个物品
G = 1 n − 1 ∑ j = 1 n ( 2 j − n − 1 ) p ( i j ) G=\frac{1}{n-1}\sum_{j=1}^n{\left( 2j-n-1 \right) p\left( i_j \right)} G=n−11j=1∑n(2j−n−1)p(ij)
from operator import itemgetter
def GiniIndex(p):
j = 1
n = len(p)
G = 0
for item, weight in sorted(p.items(), key=itemgetter(1)):
G += (2 * j - n - 1) * weight
return G / float(n - 1)
if __name__ == '__main__':
records = {'Python深度学习': 0.37,
'疯狂Java讲义': 0.32,
'C++ Primer': 0.38,
'数学之美': 0.43,
'利用Python进行数据分析': 0.54,
'浪潮之巅': 0.40,
'鸟哥的Linux私房菜': 0.07,
'机器学习': 0.33,
'高性能MySQL': 0.22,
'统计学习方法': 0.10}
print(GiniIndex(records)) # -3.16
备注:以上公式和GiniIndex()均出自《推荐系统实践》,个人感觉是错的。
更正如下:
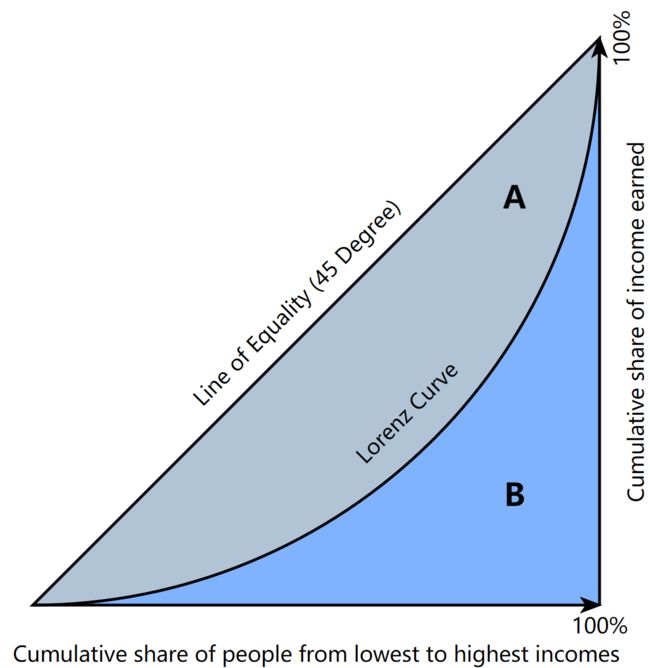
A A A、 B B B为面积
G = A A + B G=\frac{A}{A+B} G=A+BA
import numpy as np
from matplotlib import pyplot as plt
from scipy.interpolate import make_interp_spline
def GiniIndex(p):
'''基尼系数'''
cum = np.cumsum(sorted(np.append(p, 0)))
sum = cum[-1]
x = np.array(range(len(cum))) / len(p)
y = cum / sum
B = np.trapz(y, x=x)
A = 0.5 - B
G = A / (A + B)
'''绘图'''
plt.rcParams['font.sans-serif'] = ['SimHei']
fig, ax = plt.subplots()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position(('data', -0))
ax.spines['left'].set_position(('data', 0))
plt.xticks([0, 1.0])
plt.yticks([1.0])
plt.axis('scaled')
x_smooth = np.linspace(x.min(), x.max(), 100)
y_smooth = make_interp_spline(x, y)(x_smooth)
ax.plot(x_smooth, y_smooth, color='black')
ax.plot(x, x, color='black')
ax.plot([0, 1, 1, 1], [0, 0, 0, 1], color='black')
ax.fill_between(x, y)
ax.fill_between(x, x, y, where=y <= x)
ax.set_xlabel('物品')
ax.set_ylabel('流行度')
plt.show()
return G
if __name__ == '__main__':
records = {'Python深度学习': 0.37,
'疯狂Java讲义': 0.32,
'C++ Primer': 0.38,
'数学之美': 0.43,
'利用Python进行数据分析': 0.54,
'浪潮之巅': 0.40,
'鸟哥的Linux私房菜': 0.07,
'机器学习': 0.33,
'高性能MySQL': 0.22,
'统计学习方法': 0.10}
print(GiniIndex(list(records.values()))) # 0.2424050632911393

马太效应,即强者更强,弱者更弱。推荐系统初衷是让各种物品能展示给对应的感兴趣人群,但主流推荐算法如协同过滤算法具有马太效应。 G 1 G1 G1为初始用户行为计算的流行度的基尼系数, G 2 G2 G2为推荐列表计算的基尼系数,若 G 2 > G 1 G2>G1 G2>G1,则该推荐算法具有马太效应。
4. 多样性
Diversity ( R ( u ) ) = 1 − ∑ i , j ∈ R ( u ) , i ≠ j s ( i , j ) 1 2 ∣ R ( u ) ∣ ( ∣ R ( u ) ∣ − 1 ) \text{Diversity}\left( R\left( u \right) \right) =1-\frac{\sum_{i,j\in R\left( u \right) ,i\ne j}{s\left( i,j \right)}}{\frac{1}{2}|R\left( u \right) |\left( |R\left( u \right) |-1 \right)} Diversity(R(u))=1−21∣R(u)∣(∣R(u)∣−1)∑i,j∈R(u),i=js(i,j)
5. 新颖性
过滤掉有过行为的物品,或是流行度低的物品。
6. 惊喜度
略。
7. 信任度
略。
参考文献
- 推荐系统实践
- 基尼系数的计算方法与计算案例
- 推荐系统那点事儿
- 推荐系统指标评测——覆盖率与基尼系数的算法与应用
- 基尼系数如何计算? - 知乎
- matplotlib.pyplot.fill