数据预处理工作中的几个关键主题探讨：聚集、抽样、降维、离散化、变量变换等

数据预处理是数据挖掘领域必不可少的前提工作。经过预处理的功数据才更加有质量，更好地适应数据挖掘的算法过程、减少运算量或优化运算过程，在某些时候甚至起到决定结果好坏的作用。

我们讨论如下几个主题：

一、聚集

二、抽样

三、维归约（降维）

四、特征子集

五、特征创建

六、离散化和二元化

七、变量变换

---

粗略地说，我们要探讨的问题分类：对数据的分析和对数据属性的创建/修改。

有些比较简单、顾名思义的工作，就不再多赘述了。

一、聚集

聚集就是积少成多，把两个及以上的对象合并为单个对象。

有时候我们要考虑的对象很多，比如一个超市中顾客的数据，除了买了什么商品，还有商品的日期、价格、税费、时间点、日期、季节时令等等，此时我们要考虑的就是如何合并所有记录的每个属性的值。定量属性（如价格）通常使用求和、求平均等方法进行聚集；定性属性可以忽略或汇总来处理。

聚集的动机有多种：1、较小的数据集，占据较小的内存，而可以使用开销更大的算法；2、通过高层（高级别）的数据，可以起到范围或标度的转换作用；3、对象或属性群的行为通常比单个对象或单个属性的行为更加稳定（比如平均数、总数等指标往往具有较小的变异性）。

二、抽样

抽样是一种选择数据的子集进行分析的常用方法。

抽样方法：简单随机抽样，分为无放回抽样和有放回抽样。这些都是初高中的知识了。如果对象有明显的分层，则往往采用分层抽样的方法。

如何确定抽样的数量以保证数据子集能取得最好的效果，我们将在后面博文中学习、讨论。

渐进抽样：合适的样本容量很难确定。此时可以用渐进抽样（progressive sampling）或者自适应（adaptive）抽样的方法。这些方法就是从一个小容量样本开始不断增加样本容量，同时进行评估，从而最终确定下一个最佳的容量。

举个例子：

三、维归约（降维）

数据集可能包含大量的特征。进行维归约的关键好处是：如果维度较低，许多数据挖掘算法效果会更好。这一部分是因为维归约可以删除不相关的特征并降低噪声，另一部分是因为维灾难。

维灾难：随着数据维度的增加，许多数据分析变得非常困难。因为随着维度的增加，数据分布越来越稀疏。我们可以想象，如果将一个数据对象的属性变成几百维，映射到几百维的超空间里面后，每一个数据对象都有独特的每一个维度的属性值，那么数据的分布就会显得稀疏，这对分类模型而言就造成了很大的困难。可以想到，我们寻找一个SVM超平面都比较困难了，更何况高维数据的分类。而对于聚类，对于基于密度或者距离的算法就失去了意义。所以维灾难情况下，分类准确率越来越低，聚类质量也下降了很多。

维灾难可以用一些线性代数的方法来解决，比如现在非常非常流行的PCA、PLS等。可以笔者的博文《主成分分析（PCA）的线性代数推导过程》、《降维和特征选择的关键方法介绍及MATLAB实现》。还有奇异值分解（SVD）《矩阵的特征分解和奇异值（SVD）分解——求法和意义》也可以用在维归约。

笔者的实验室主要做一些水质数据、光谱数据的处理，在降维环节中都常常用到PCA，甚至笔者自己在做图像领域，对提取多维特征也可用PCA降维讨论，降维的手段在各个数据处理的领域具有普适性，也是大数据时代很有意义的前提工作，应当引起重视。

维归约的另一个好处是：可以使得模型更容易理解。因为模型只涉及到较少的属性。此外，降维后也让数据的可视化更容易实现。

四、特征子集

降低维度的另一种方法是仅仅使用特征的一个子集。这个方法看起来是会丢失很多信息，但是当存在冗余或者不相关特征的时候是很有用的。比如前面提到的商店的例子，顾客购买行为数据有时间、税费、价格、地点、商品编号等等，其中，商品ID我们是不care的，税费可以用税率计算，其实也不需要，这些特征集合就是冗余的特征完全可以丢弃掉。

上面这个例子中我们丢弃特征的方法使用的是传统的人工筛选，在人工智能中我们可能可以称为“专家系统”。这样子虽然往往比较有效，但是还是需要系统的方法来帮助我们选择特征子集。比如说，最笨的方法就是把n个属性组成2^n个子集，一个个遍历输入算法，看哪个结果最好就选哪个。这也是最理想化的方法。但这种遍历方法运算量太大，耗时多，显然不是一种值得推广的方法。

有三种标准的特征子集的选择方法：嵌入、过滤和包装 方法。

嵌入方法：在算法运行期间，由算法本身决定使用哪些属性、忽略哪些属性。例如决策树分类器就是这样方式运行。

过滤方法：使用某种独立于数据挖掘任务的方法，在算法运行前进行特征选择。

包装方法：将算法作为黑盒，使用类似于前面介绍的理想主义的遍历方法。但是包装方法中通常并不枚举所有可能的子集，而是有选择、有方向的抽样包装评估。

特征选择的过程由四部分组成：子集评估度量、控制新的特征子集产生的搜索策略、停止搜索判断和验证过程。

评估：根据当前选择的子集评价当前的特征子集。这需要一种评估度量，来确定子集的质量。

搜索策略：花费尽可能低，且找到最优或者近似最优的特征子集。这两个要求往往是矛盾的，所以需要折中权衡。

停止搜索策略：因为子集数量大，不可能考虑所有子集，所以需要停止搜索的策略。一般来说，可以是：迭代次数、阈值，等等。比如设计10000次epoch，或者当误差eps小于某个值，则停止搜索。这些在深度学习、基于模型的聚类里面也常常会用到。

验证：验证目标算法在选定子集上的效果。

特征加权是另一种保留或者删除特征的方法。对每个特征都赋予一个权值，具有较大权值的特征在模型中所起的作用更加重要。

五、特征创建

1、特征提取

按照数据对象的物理意义表征，提取一些具体的特征，如图像中的颜色特征、纹理特征等直观、且具有含义的特征；或者对数据进行处理，抽象出一些高层次的特征，如CNN。

2、数据映射

将数据映射的其他空间后可能展现出不一样的重要分布或者有趣的特征。例如，时间序列信号，可以做傅里叶变换、小波变换到频域，这样有助于减轻噪声的影响，发现周期性规律。

在之前讲SVM的博文《简单粗暴理解支持向量机（SVM）及其MATLAB实例》中也讲到，SVM可以帮助我们把数据从低维空间映射到高维空间，从而使得他们容易被分开。

3、特征构造

有时候原始数据的特征的形式不适合数据挖掘算法。构造一个或多个原特征构造的新特征可能比原特征更有用。

六、离散化和二元化

有些算法要求数据是分类属性形式。发现关联模式的算法要求数据是二元属性形式。因此需要将连续属性变换成分类属性（离散化），并且连续和离散属性都要变换成一个或多个二元属性。

二元化

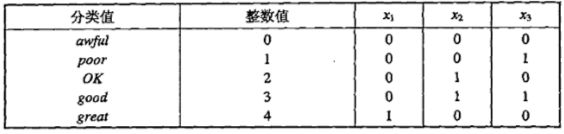
如下图，我们对5个类别，用3个二元属性来表征。

但是上表中，二元属性中是有相关性的，比如x2和x3是有相关性的，因为出现good时x2和x3都为1。

关联分析中，需要非对称的二元属性，而且我们只关注出现1值的二元属性。所以要给每一个分类引入一个二元属性。这样可能会占用更多的内存。

离散化

离散化涉及到2个子任务：多少个分割点、分割位置。

下面我们看看非监督离散化和监督离散化。

七、变量变换

两种重要的变量变换类型：简单函数变换和规范化。

1、简单函数：

但是也要注意，简单函数变换可能会改变数据的特性，在变换时要考虑到这个问题。例如，1/x虽然压缩了大于1的值，但是却放大了0和1之间的值。且1/x的变换逆转了排序。

2、规范化或标准化

标准化是我们经常会用到的，很重要。比如深度学习中用到的批标准化。见《TensorFlow实现Batch Normalization详解和代码实现》，你可以直观、生动地了解到标准化有什么用。

需要注意的是，均值和标准差受离群点的影响很大，因此，数据中存在离群点时，通常用中位数取代均值，用绝对标准差取代标准差。