著名字符串匹配算法:KMP算法原理分析和代码实现
核心思想
KMP 算法,全称是 Knuth Morris Pratt 算法,核心思想与 BM 算法类似,假设现在有主串A,模式串B,在主串中查找模式串,在遇到不可匹配字符时,希望通过一些规律,使得模式串可以多向后滑动几位以加快匹配速度。
如图,主串和模式串在匹配时遇到坏字符时,可以发现模式串往后移动一位或两位,第一个字符便不匹配,而滑动三位则正好匹配了,因此,考虑是否存在一种规则,通过遇到坏字符时的其他已知条件来推导最大滑动位数。
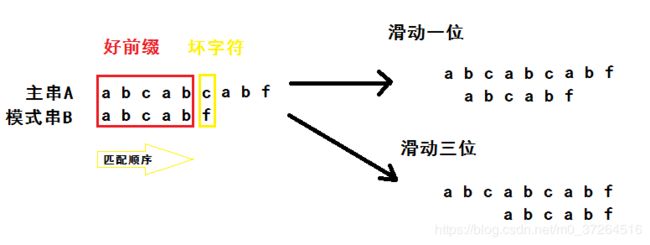
KMP 基本原理
当遇到坏字符时,已知的条件有好前缀,当模式串往后移动并继续匹配时,可以发现其实就是好前缀的后缀子串与它的前缀子串在匹配,如图:
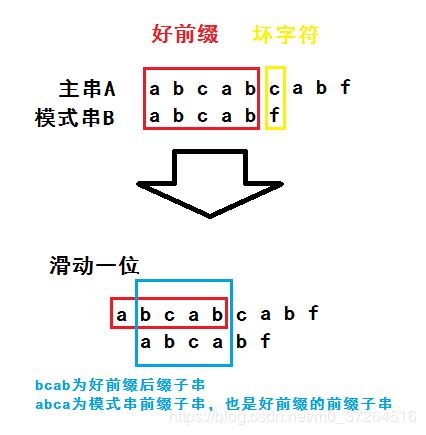
所以我们可以通过好前缀来找到一些规律,也就是要求好前缀的前缀子串与后缀子串能够匹配的,并且是最长的那个子串,即最长可匹配前缀子串,也是最长可匹配后缀子串。
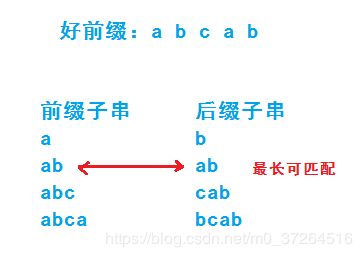
在匹配时,可以通过好前缀的最长可匹配前后子串,滑动至最长可匹配前后子串对应的位置继续向后匹配:

通过列举好前缀的前后缀子串,可以发现,其实好前缀就是模式串的前缀子串,在计算最长可匹配子串时,与主串没有关系,所以,我们可以事先对模式串进行预处理,通过最长可匹配子串计算出模式串中任意一位作为坏字符位置时,模式串的滑动位数,存储这个位数的数组就是 next 数组。
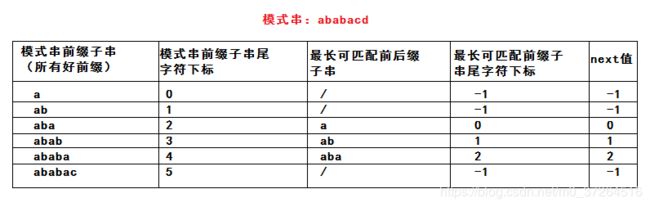
KMP 算法代码:
// str, model 分别是主串和模式串;n, m 分别是主串和模式串的长度。
public static int kmp(char[] str, int n, char[] model, int m) {
int[] next = getNexts(model, m);
int j = 0;
for (int i = 0; i < n; ++i) {
if (str[i] == model[j]) {//从前往后进行匹配
++j;
}
if (j == m) { // 找到匹配模式串的了
return i - m + 1;
}
while (j > 0 && str[i] != model[j]) { // 遇到坏字符,利用next数组计算j的位置,直到str[i]与model[j]匹配或第一个字符也不匹配时,
j = next[j - 1] + 1;
}
}
return -1;
}
next 数组计算方法
暴力匹配法:将模式串每个前缀子串与其所有后缀子串进行匹配,可得到 next 数组,但是效率太低。
利用动态规划思想计算:
当我们计算 next[i] 时,next[0] ~ next[i-1] 的值已经计算出来了,思考是否可以通过已知值来计算 next[i] 的值呢?
情况一:若 next[i-1] = k-1,则表示i-1所代表的前缀子串的最长可匹配前缀子串尾字符位置是k-1,因此可以比较model[k]是否与model[i]相等,若相等,则next[i]=k

情况二:若情况一中的model[k]与model[i]不相等时,该如何计算呢?
假设model[0~i]的最长可匹配子串是model[r~i],则model[r~i-1]必定是model[0~i-1]的可匹配后缀子串,所以,我们可以通过考察model[r~i-1]的次长可匹配后缀子串对应的可匹配前缀子串model[0~x]的下一个字符是否等于model[i],若是,则model[0~x]是所求的最长可匹配子串。
次长可匹配后缀子串肯定包含于最长可匹配后缀子串,而最长可匹配后缀子串与最长可匹配前缀子串对应,因此,就是求最长可匹配前缀子串的最长可匹配后缀子串。
计算 next 数组代码:
// model 表示模式串,m 表示模式串的长度
private static int[] getNexts(char[] model, int m) {
int[] next = new int[m];
next[0] = -1;
int k = -1;
for (int i = 1; i < m; ++i) {
while (k != -1 && model[k + 1] != b[i]) {//情况二
k = next[k];
}
if (model[k + 1] == model[i]) {//符合情况一
++k;
}
next[i] = k;
}
return next;
}
KMP 算法代码实现
// model 表示模式串,m 表示模式串的长度
private static int[] getNexts(char[] model, int m) {
int[] next = new int[m];
next[0] = -1;
int k = -1;
for (int i = 1; i < m; ++i) {
while (k != -1 && model[k + 1] != b[i]) {//情况二
k = next[k];
}
if (model[k + 1] == model[i]) {//符合情况一
++k;
}
next[i] = k;
}
return next;
}
// str, model 分别是主串和模式串;n, m 分别是主串和模式串的长度。
public static int kmp(char[] str, int n, char[] model, int m) {
int[] next = getNexts(model, m);
int j = 0;
for (int i = 0; i < n; ++i) {
if (str[i] == model[j]) {//从前往后进行匹配
++j;
}
if (j == m) { // 找到匹配模式串的了
return i - m + 1;
}
while (j > 0 && str[i] != model[j]) { // 遇到坏字符,利用next数组计算j的位置,直到str[i]与model[j]匹配或第一个字符也不匹配时,
j = next[j - 1] + 1;
}
}
return -1;
}