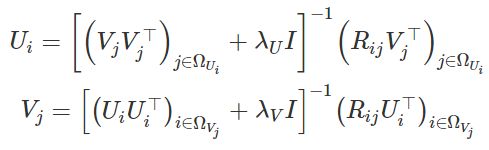推荐系统的PMF - 概率矩阵分解和协同过滤

自动化推荐系统通常用于根据现有的偏好数据为用户提供他们感兴趣的产品建议。 文献中通常描述了不同类型的推荐系统。我们这篇文章将突出介绍两个主要类别，然后在第二个类别上进一步扩展：

基于内容的过滤：这些过滤器利用用户偏好来做出新的预测。 当用户提供有关其偏好的明确信息时，系统会记录并使用这些信息来自动提出建议。 我们日常使用的许多网站和社交媒体都属于此类。

协同过滤：当用户提供的信息不足以提出项目建议时，会发生什么情况？ 在这些情况下，我们可以使用其他用户提供的具有相似首选项的数据。 此类别中的方法利用了一组用户的过去选择历史来得出建议。

在第一种情况下，期望给定的用户建立一个清楚表明偏好的配置文件，在第二种情况下，此信息可能无法完全使用，但是我们希望我们的系统仍能够基于类似的证据提出建议 用户提供。 一种称为概率矩阵分解的方法（简称为PMF）通常用于协同过滤，并且将成为本文其余部分讨论的主题。 现在让我们深入研究此算法的细节及其直觉。

概率矩阵分解解释

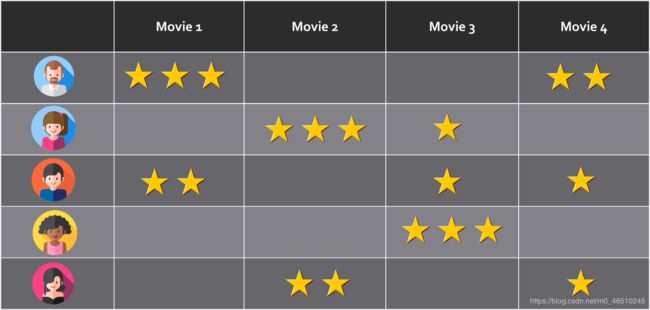
假设我们有一组用户u1，u2，u3…uN，他们对一组项目v1，v2，v3…vM进行评分。 然后，我们可以将评分构建为N行和M列的矩阵R，其中N是用户数，M是要评分的项目数。

评分映射。 可以将其视为每个用户（行）对多个项目（列）进行评分的矩阵

R矩阵的一个重要特征是它是稀疏的。 也就是说，仅其某些单元格具有非空的评级值，而其他单元格则没有。 对于给定的用户A，系统应该能够基于他/她的偏好以及类似用户的选择来提供项目推荐。 但是，用户A不必明确推荐某项就可以对其进行推荐。 具有相似首选项的其他用户将弥补有关用户A的缺失数据。这就是为什么概率矩阵分解属于协同过滤推荐系统的类别。

让我们考虑一下电影推荐系统。 想象一下，如果我们被要求观看和评价特定季节中放映的每部电影会是什么样子。 那是不切实际的，不是吗？ 我们根本没有时间这样做。

鉴于并非所有用户都能够对所有可用项目进行评分，我们必须找到一种方法来填补R矩阵的信息空白，并且仍然能够提供相关建议。 PMF通过利用类似用户提供的评级来解决此问题。 从技术上讲，它利用了贝叶斯学习的一些原理，这些原理也适用于我们缺少或不完整数据的其他情况。

可以通过使用两个低阶矩阵U和V来估计R矩阵，如下所示：

此处，UT是一个NxD矩阵，其中N是注册用户数，D是等级。 V是DxM矩阵，其中M是要评估的项目数。 因此，NxM评级矩阵R可以通过以下方式近似：

公式1：R表达式

从现在开始，我们的工作是找到UT和V，它们将反过来成为模型的参数。 因为U和V是低阶矩阵，所以PMF也被称为低阶矩阵分解问题。 此外，U和V矩阵的这一特殊特征使得PMF甚至对于包含数百万条记录的数据集也可扩展。

PMF从贝叶斯学习中得出的直觉用于参数估计。 一般而言，我们可以说在贝叶斯推断中，我们的目的是借助贝叶斯规则来找到模型参数的后验分布：

公式2：参数的贝叶斯规则

在这里，X是我们的数据集，θ是分布的参数或参数集。 α是分布的超参数。 p（θ| X，α）是后验分布，也称为后验分布。 p（X |θ，α）是似然，p（θ|α）是先验。 训练过程的整体思路是，随着我们获得有关数据分布的更多信息，我们将调整模型参数θ以适合数据。 从技术上讲，后验分布的参数将插入到先前的分布中，以进行训练过程的下一次迭代。 也就是说，给定训练步骤的后验分布最终将成为下一步骤的先验。 重复该过程，直到步骤之间的后验分布p（θ| X，α）几乎没有变化为止。

现在，让我们回到有关PMF的直觉上。 如前所述，我们的模型参数将是U和V，而R将是我们的数据集。 经过培训后，我们将得到一个修订的R *矩阵，该矩阵还将包含对用户项目单元格最初在R中为空的评分。我们将使用此修订的评分矩阵进行预测。 基于这些考虑，我们将拥有：

其中σ是零均值球形高斯分布的标准偏差。 然后，通过替换等式2中的这些表达式，我们将得到：

由于U和V矩阵彼此独立（用户和项独立发生），因此该表达式也可以这样写：

公式3：PMF的A-Posteriori分布

现在是时候找出该方程式的每个分量了。 首先，似然函数由下式给出：

公式4：观测等级的分布

在此，I {ij}是一个指标，当第i行和第j列的评级存在时，其值为1，否则为0。 如我们所见，此分布是具有以下参数的spherical Gaussian分布：

反过来，U和V的先验分布由下式给出：

公式5和6：U和V的先验分布

这是两个零均值球面高斯（spherical Gaussians）。 然后，通过在3中替换4、5和6，我们将得到：

为了训练我们的模型，我们将寻求通过将参数U和V的导数等价为零来最大化此函数。 但是，由于高斯函数中的exp函数，这样做将非常困难。 为了克服这个问题，我们应该将对数应用于前面的方程式的两边，然后应用所需的导数。 因此，通过将对数应用于上一个方程的两边，我们将获得：

这是一个更容易区分的表达方式。 我们也知道，根据定义，高斯PDF由以下公式给出：

因此，我们对数后验的表达式将如下所示（注意：为简单起见，我们已删除了常量）：

Fro后缀表示Frobenius范数，它由下式给出：

最后，通过引入一些附加的符号来标识模型的超参数，我们将获得：

公式7：PMF的对数后验

然后，通过对参数微分方程式7并将导数等于零，我们将得到：

从这里，我们可以导出表达式以更新Ui和Vj：

公式8和9：用于更新U和V的表达式

假设λU和λV都不为零，则可以保证所涉及的逆矩阵存在。 作为训练过程的一部分，我们将迭代更新Ui和Vj。 一旦找到最佳值，就可以使用方程式7获得log-MAP的值（最大后验值）。正如我们在Python实现中所看到的那样，我们可以使用该值来监控训练收敛 。

用Python实现

为了进行训练，我们使用了IMDB电影数据库的一个子集，然后将其分为两部分分别进行训练和验证。

初始化：为了初始化V，我们从零均值高斯绘制随机数，标准偏差为1 /λV。 此外，等级值D被设置为较小的值10。

def initialize_parameters(lambda_U, lambda_V):
    U = np.zeros((n_dims, n_users), dtype=np.float64)
    V = np.random.normal(0.0, 1.0 / lambda_V, (n_dims, n_movies))
    
    parameters['U'] = U
    parameters['V'] = V
    parameters['lambda_U'] = lambda_U
    parameters['lambda_V'] = lambda_V

更新参数：为了更新U和V，我们使用公式8和9：

def update_parameters():
    U = parameters['U']
    V = parameters['V']
    lambda_U = parameters['lambda_U']
    lambda_V = parameters['lambda_V']
    
    for i in range(n_users):
        V_j = V[:, R[i, :] > 0]
        U[:, i] = np.dot(np.linalg.inv(np.dot(V_j, V_j.T) + lambda_U * np.identity(n_dims)), np.dot(R[i, R[i, :] > 0], V_j.T))
        
    for j in range(n_movies):
        U_i = U[:, R[:, j] > 0]
        V[:, j] = np.dot(np.linalg.inv(np.dot(U_i, U_i.T) + lambda_V * np.identity(n_dims)), np.dot(R[R[:, j] > 0, j], U_i.T))
        
    parameters['U'] = U
    parameters['V'] = V

计算对数后验：对数后验由公式7给出：

def log_a_posteriori():
    lambda_U = parameters['lambda_U']
    lambda_V = parameters['lambda_V']
    U = parameters['U']
    V = parameters['V']
    
    UV = np.dot(U.T, V)
    R_UV = (R[R > 0] - UV[R > 0])
    
    return -0.5 * (np.sum(np.dot(R_UV, R_UV.T)) + lambda_U * np.sum(np.dot(U, U.T)) + lambda_V * np.sum(np.dot(V, V.T)))

训练循环：要训练模型，我们调用先前的函数并监视对数后验以及在训练和测试集上评估的RMSE（均方根误差）：

def train(n_epochs):
    initialize_parameters(0.3, 0.3)
    log_aps = []
    rmse_train = []
    rmse_test = []

    update_max_min_ratings()
    rmse_train.append(evaluate(train_set))
    rmse_test.append(evaluate(test_set))
    
    for k in range(n_epochs):
        update_parameters()
        log_ap = log_a_posteriori()
        log_aps.append(log_ap)

        if (k + 1) % 10 == 0:
            update_max_min_ratings()

            rmse_train.append(evaluate(train_set))
            rmse_test.append(evaluate(test_set))
            print('Log p a-posteriori at iteration', k + 1, ':', log_ap)

    update_max_min_ratings()

    return log_aps, rmse_train, rmse_test

我们将训练循环运行150次迭代，结果如下：

在左侧，我们可以看到在训练模型时对数后验如何演变。 在右侧，我们可以看到在训练集和测试集上评估的RMSE值。 考虑到R预测可能超出额定值的0-5范围，我们使用线性插值法确保R值受此间隔限制。 原始论文[1]提出了其他方法，例如使用逻辑函数和线性插值。 对于训练，还建议使用带动量的梯度下降来处理较大的数据集。

最后，以下是数据库中用户ID为45的电影推荐：

结论

PMF是用于协作过滤的强大算法。 它利用具有相似首选项的用户提供的数据向特定用户提供推荐。 它也被称为低秩矩阵分解方法，因为它使用低秩矩阵来估计等级R矩阵，然后进行有用的预测。

引用

[1] Salakhutdinov, Ruslan & Mnih, Andriy. Probabilistic Matrix Factorization. In NIPS’07: Proceedings of the 20th International Conference on Neural Information Processing Systems, pages 1257–1264, 2007.

[2] Brooks-Bartlett Jonny. Probability concepts explained: Bayesian inference for parameter estimation.

作者：Oscar Contreras Carrasco