【数据结构与算法】内部排序之三:堆排序(含完整源码)
转载请注明出处:http://blog.csdn.net/ns_code/article/details/20227303
前言
堆排序、快速排序、归并排序(下篇会写这两种排序算法)的平均时间复杂度都为O(n*logn)。要弄清楚堆排序,就要先了解下二叉堆这种数据结构。本文不打算完全讲述二叉堆的所有操作,而是着重讲述堆排序中要用到的操作。比如我们建堆的时候可以采用堆的插入操作(将元素插入到适当的位置,使新的序列仍符合堆的定义)将元素一个一个地插入到堆中,但其实我们完全没必要这么做,我们有执行操作更少的方法,后面你会看到,我们基本上只用到了堆的删除操作,更具体地说,应该是删除堆的根节点后,将剩余元素继续调整为堆的操作。先来看二叉堆的定义。
二叉堆
二叉堆其实是一棵有着特殊性质的完全二叉树,这里的特殊性质是指:
1、二叉堆的父节点的值总是大于等于(或小于等于)其左右孩子的值;
2、每个节点的左右子树都是一棵这样的二叉堆。
如果一个二叉堆的父节点的值总是大于其左右孩子的值,那么该二叉堆为最大堆,反之为最小堆。我们在排序时,如果要排序后的顺序为从小到大,则需选择最大堆,反之,选择最小堆,这点通过后面对堆排序分析,你会有所体会。
堆排序
由二叉堆的定义可知,堆顶元素(即二叉堆的根节点)一定为堆中的最大值或最小值,因此如果我们输出堆顶元素后,将剩余的元素再调整为二叉堆,继而再次输出堆顶元素,再将剩余的元素调整为二叉堆,反复执行该过程,这样便可输出一个有序序列,这个过程我们就叫做堆排序。
由于我们的输入是一个无序序列,因此要实现堆排序,我们要先后解决如下两个问题:1、如何将一个无序序列建成一个二叉堆;
2、在去掉堆顶元素后,如何将剩余的元素调整为一个二叉堆。
针对第一个问题,可能很明显会想到用堆的插入操作,一个一个地插入元素,每次插入后调整元素的位置,使新的序列依然为二叉堆。这种操作一般是自底向上的调整操作,即先将待插入元素放在二叉堆后面,而后逐渐向上将其与父节点比较,进而调整位置。但正如前言中所说,我们完全用不着一个节点一个节点地插入,那我们要怎么做呢?我们需要先来解决第二个问题,解决了第二个问题,第一个问题问题也就迎刃而解了。
调整二叉堆
要分析第二个问题,我们先给出以下前提:
1、我们排序的目标是从小到大,因此我们用最大堆;
2、我们将二叉堆中的元素以层序遍历后的顺序保存在一维数组中,根节点在数组中的位置序号为0。
这样,如果某个节点在数组中的位置序号为i,那么它的左右孩子的位置序号分别为2i+1和2i+2。
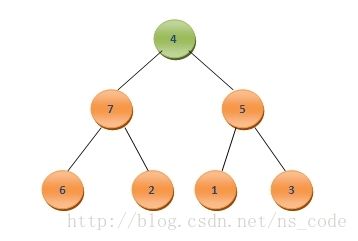
为了使调整过程更易于理解,我们采用如下二叉堆来分析(注意下面的分析,我们并没有采用额外的数组来存储每次去掉的堆顶数据):
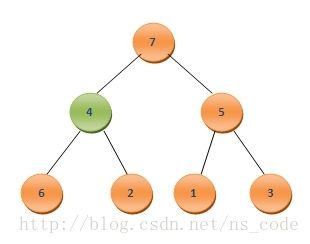
这里数组A中元素的个数为8,很明显最大值为A0,为了实现排序后的元素按照从小到大的顺序排列,我们可以将二叉堆中的最后一个元素A7与A0互换,这样A7中保存的就是数组中的最大值,而此时该二叉树变为了如下情况:
为了将其调整为二叉堆,我们需要寻找4应该插入的位置。为此,我们让4与它的孩子节点中最大的那个,也就是其左孩子7,进行比较,由于4<7,我们便把二者互换,这样二叉树便变成了如下的形式:
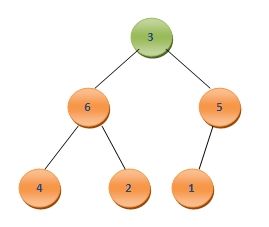
接下来,继续让4与其左右孩子中的最大者,也就是6,进行比较,同样由于4<6,需要将二者互换,这样二叉树变成了如下的形式:
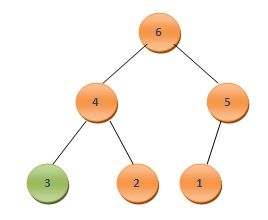
这样便又构成了二叉堆,这时候A0为7,是所有元素中的最大元素。同样我们此时继续将二叉堆中的最后一个元素A6和A0互换,这样A6中保存的就是第二大的数值7,而A0就变为了3,形式如下:
为了将其调整为二叉堆,一样将3与其孩子结点中的最大值比较,由于3<6,需要将二者互换,而后继续和其孩子节点比较,需要将3和4互换,最终再次调整好的二叉堆形式如下:
一样将A0与此时堆中的最后一个元素A5互换,这样A5中保存的便是第三大的数值,再次调整剩余的节点,如此反复,直到最后堆中仅剩一个元素,这时整个数组便已经按照从小到大的顺序排列好了。
据此,我们不难得出将剩余元素继续调整为二叉堆的操作实现代码如下(同前面两篇博文中一样,我们不需每次比较后都交换元素位置,代码中可以再次体会到这点):
/*
arr[start+1...end]满足最大堆的定义,
将arr[start]加入到最大堆arr[start+1...end]中,
调整arr[start]的位置,使arr[start...end]也成为最大堆
注:由于数组从0开始计算序号,也就是二叉堆的根节点序号为0,
因此序号为i的左右子节点的序号分别为2i+1和2i+2
*/
void HeapAdjustDown(int *arr,int start,int end)
{
int temp = arr[start]; //保存当前节点
int i = 2*start+1; //该节点的左孩子在数组中的位置序号
while(i<=end)
{
//找出左右孩子中最大的那个
if(i+1<=end && arr[i+1]>arr[i])
i++;
//如果符合堆的定义,则不用调整位置
if(arr[i]<=temp)
break;
//最大的子节点向上移动,替换掉其父节点
arr[start] = arr[i];
start = i;
i = 2*start+1;
}
arr[start] = temp;
}
//进行堆排序
for(i=len-1;i>0;i--)
{
//堆顶元素和最后一个元素交换位置,
//这样最后的一个位置保存的是最大的数,
//每次循环依次将次大的数值在放进其前面一个位置,
//这样得到的顺序就是从小到大
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
//将arr[0...i-1]重新调整为最大堆
HeapAdjustDown(arr,0,i-1);
}
建立二叉堆
搞懂了第二个问题,那么我们回过头来看如何将无序的数组建成一个二叉堆。
我们同样以上面的数组为例,假设其数组内元素的原始顺序为:A[]={6,1,3,9,5,4,2,7},那么在没有建成二叉堆前,个元素在该完全二叉树中的存放位置如下:
这里的后面四个元素均为叶子节点,很明显,这四个叶子可以认为是一个堆(因为堆的定义中并没有对左右孩子间的关系有任何要求,所以可以将这几个叶子节点看做是一个堆),而后我们便考虑将第一个非叶子节点9插入到这个堆中,再次构成一个堆,接着再将3插入到新的堆中,再次构成新堆,如此继续,直到该二叉树的根节点6也插入到了该堆中,此时构成的堆便是由该数组建成的二叉堆。因此,我们这里同样可以利用到上面所写的HeapAdjustDown(int *,int,int)函数,因此建堆的代码可写成如下的形式:
//把数组建成为最大堆
//第一个非叶子节点的位置序号为(len-1)/2
for(i=(len-1)/2;i>=0;i--)
HeapAdjustDown(arr,i,len-1); 如果还不是很明白,注意读下HeapAdjustDown(int *,int,int)函数代码中关于该函数作用的注释。
完整源码
最后贴出完整源码:
/*******************************
堆排序
Author:兰亭风雨 Date:2014-02-27
Email:[email protected]
********************************/
#include
#include
/*
arr[start+1...end]满足最大堆的定义,
将arr[start]加入到最大堆arr[start+1...end]中,
调整arr[start]的位置,使arr[start...end]也成为最大堆
注:由于数组从0开始计算序号,也就是二叉堆的根节点序号为0,
因此序号为i的左右子节点的序号分别为2i+1和2i+2
*/
void HeapAdjustDown(int *arr,int start,int end)
{
int temp = arr[start]; //保存当前节点
int i = 2*start+1; //该节点的左孩子在数组中的位置序号
while(i<=end)
{
//找出左右孩子中最大的那个
if(i+1<=end && arr[i+1]>arr[i])
i++;
//如果符合堆的定义,则不用调整位置
if(arr[i]<=temp)
break;
//最大的子节点向上移动,替换掉其父节点
arr[start] = arr[i];
start = i;
i = 2*start+1;
}
arr[start] = temp;
}
/*
堆排序后的顺序为从小到大
因此需要建立最大堆
*/
void Heap_Sort(int *arr,int len)
{
int i;
//把数组建成为最大堆
//第一个非叶子节点的位置序号为len/2-1
for(i=len/2-1;i>=0;i--)
HeapAdjustDown(arr,i,len-1);
//进行堆排序
for(i=len-1;i>0;i--)
{
//堆顶元素和最后一个元素交换位置,
//这样最后的一个位置保存的是最大的数,
//每次循环依次将次大的数值在放进其前面一个位置,
//这样得到的顺序就是从小到大
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
//将arr[0...i-1]重新调整为最大堆
HeapAdjustDown(arr,0,i-1);
}
}
int main()
{
int num;
printf("请输入排序的元素的个数:");
scanf("%d",&num);
int i;
int *arr = (int *)malloc(num*sizeof(int));
printf("请依次输入这%d个元素(必须为整数):",num);
for(i=0;i
总结
最后我们简要分析下堆排序的时间复杂度。我们在每次重新调整堆时,都要将父节点与孩子节点比较,这样,每次重新调整堆的时间复杂度变为O(logn),而堆排序时有n-1次重新调整堆的操作,建堆时有((len-1)/2+1)次重新调整堆的操作,因此堆排序的平均时间复杂度为O(n*logn)。由于我们这里没有借用辅助存储空间,因此空间复杂度为O(1)。
堆排序在排序元素较少时有点大才小用,待排序列元素较多时,堆排序还是很有效的。另外,堆排序在最坏情况下,时间复杂度也为O(n*logn)。相对于快速排序(平均时间复杂度为O(n*logn),最坏情况下为O(n*n)),这是堆排序的最大优点。