Canvas：使用JavaScript进行基本图形操作与处理

1.图像数据的相关接口

由于HTML5引入了 canvas 标签，这大大简化了JavaScript处理图像的工作。通过canvas ，JavaScript可以对图像进行像素级的操作，甚至还可以直接处理图像的二进制原始数据，这为图像的签名技术提供了支持。另外 canvas 还提供了常用的图像格式转换功能，可以使用JavaScript简单快捷地更改图像的编码方式。

出于安全考虑，浏览器通常不允许处理跨域图像，但利用特殊的手段是可以突破这一限制的。解决处理跨域图像出现的安全警告的方法是使用CORS（Cross-Origin Resource Sharing），具体可以参加 http://www.w3.org/TR/cors/ 。

利用 FileReader 和 canvas 相配合，可以读取本地图像文件，比如我们有如下HTML代码：

<canvas id="myCanvas">抱歉，您的浏览器还不支持canvas。canvas>
<input type="file" id="myFile" />

这两行HTML代码包含一个 id 为 myCanvas 的 canvas 画布，还包含一个 id为 myFile 的文件选择控件，我们将通过文件选择控件为用户提供选择本地文件的接口，然后利用 canvas 画布为JavaScript提供图像处理的接口。

下面通过JavaScript为这两个元素绑定事件。为了方便引用，先用两个变量来存储这两个元素：

var myCanvas = document.getElementById('myCanvas');
var myFile = document.getElementById('myFile');

当用户选定一个文件时，我们就应开始通过 FileReader 读取文件数据，为此监视 myFile 的 onchange 事件，并构造 FileReader ：

file.onchange = function(event) {
    var selectedFile = event.target.files[0];
var reader = new FileReader();
    reader.onload = putImage2Canvas;
    reader.readAsDataURL(selectedFile);
}

在这段代码中， onchange 事件被激活时会传递一个 event 参数给处理函数，event 的 target 子属性是一个描述当前文件选择控件的对象，其 files 属性是一个描述用户已选文件信息的数组。 files 是数组类型是因为HTML5支持一次选择多个文件，如果文件选择控件没有开启多选模式，那么此数组只有一个元素。

接下来创建了一个 FileReader 对象，将其保存在 reader 中。reader.onload 事件定义了文件加载完成后的操作， reader.readAsDataURL将文件内容读取成Data URL。

接下来编写 putImage2Canvas 函数，这个函数用来将 FileReader 读取的数据放入 canvas 中供JavaScript处理：

function putImage2Canvas(event) {
  var img = new Image();
  img.src = event.target.result;
  img.onload = function(){
    myCanvas.width = img.width;
    myCanvas.height = img.height;
    var context = myCanvas.getContext('2d');
    context.drawImage(img, 0, 0);
    var imgdata = context.getImageData(0, 0, img.width, img.height);
    // 处理imgdata
  }
}

event 是 reader.onload 传递的参数， event.target.result 是FileReader 读取的结果，由于之前我们将文件内容以Data URL的方式读取，所以可以直接将读取结果作为 src 创建图像对象。

当图像创建完毕后， img.onload 事件被激活，此时我们将 canvas 的尺寸设置成图像的尺寸，然后通过 drawImage 将图像画在画布上，最后通过getImageData 获取图像像素数据供JavaScript处理。

下面我们来详细了解下 drawImage 和 getImageData 这两个方法，这两个方法将会在后面的章节中一直用到，是JavaScript处理图像用到的最基本的方法。

drawImage 有三种用法，第一种是只指定图片的绘制位置：

context.drawImage(img, x, y);

这也是本节开始的代码实例中用到的使用方法，这种方法会将图片左上角置于坐标相对于画布的 (x, y) 点上，如果画布尺寸足够则画出整个图像，否则将超出画布的部分舍弃，如图1-1。

图1-1 超出画布部分的图像会被舍弃 1

1 图像来自Wikipedia，由Pamri上传。

drawImage 的第二种方法是指定指定图片绘制位置的同时图像的尺寸：

context.drawImage(img, x, y, width, height);

新绘制的图像会根据指定的尺寸进行放大或缩小，如图1-2。

图1-2 利用 drawImage 缩放图像

drawImage 的第三种用法是截取图片的一部分进行绘制：

context.drawImage(img, sx, sy, swidth, sheight, x, y, width, height);

sx 和 sy 指定图像被截取部分左上角在图片上的坐标， swidth 和 sheight指定图像被截取部分的尺寸， x 和 y 指定图像被截取部分画在画布上的位置，width 和 height 指定图像被截取部分在画布上重绘的尺寸。图1-3中利用drawImage 截取了图像的一部分并画在了画布上。

图1-3 利用 drawImage 截取图片的一部分

getImageData 方法用来获取 canvas 画布中图像的像素数据，使用方法比较简单，只需指定要获取图像左上角的位置和尺寸即可：

context.getImageData(x, y, width, height);

返回的数据是一个对象，此对象包含三个属性，分别是 data 、 width 和height ，其中 data 就是图像的像素数据。 data 是一个一维数组，顺次记录着每个像素点的RGBA信息。R代表红色，G代表绿色，B代表蓝色，A代表不透明度，其取值范围均为0-255。对于A，0代表完全透明，255代表完全不透明。

由于 data 是一个一维数组，所以在处理数据时应以每4个元素为单位读取 data：

for(var i=0, len=imgdata.data.length; i<len; i+=4) {
    var r = imgdata.data[i],
      g = imgdata.data[i+1],
      b = imgdata.data[i+2],
      a = imgdata.data[i+3];
    // 处理像素数据
}

比如最简单的反色操作，我们可以通过以下代码实现：

for(var i=0, len= imgdata.data.length; i<len; i+=4) {
    imgdata.data[i] = 255-imgdata.data[i];
    imgdata.data[i+1] = 255-imgdata.data[i+1];
    imgdata.data[i+2] = 255-imgdata.data[i+2];
}

由于反色无需对图像的不透明度进行处理，所以我们只处理了R、G和B的数据。

数据处理完毕后可以通过 putImageData 将处理结果输出到画布上：

putImageData(imgdata, x, y);

最后的处理结果如图1-4所示。

图1-4 通常操作图像像素数据反色处理图像

toDataURL 方法可以将 canvas 画布中的图像保存为图片：

var imgsrc = myCanvas.toDataURL();
var img = document.create('img');
img.src = imgsrc;

toDataURL 默认将图像转换为PNG图片，但也可以保存为JPEG图片：

var imgsrc = myCanvas.toDataURL('image/jpeg');

如果保存为JPEG图片，还可以通过第二个参数指定图片质量：

var imgsrc = myCanvas.toDataURL('image/jpeg', quality);

quality 的取值范围为0.0-1.0，0.0代表图片质量最差，1.0代表图片质量最好。

此外，Chrome浏览器还支持转换为WebP图像：

var imgsrc = myCanvas.toDataURL('image/webp');

2.图像几何变换

得益于HTML5完善的图像处理接口，在对图像进行几何变换时，我们并不需要单独操作每个像素点，下面将对图像平移、图像缩放、镜像变换、图像旋转和图像转置的实现逐一讲解。

2.1图像平移

canvas 通过 translate 方法实现图像平移。注意， translate 平移的是canvas 画布的坐标，并不会改变画布上已有图像的位置。

translate 的用法非常简单，只需指定 canvas 画布左上角平移后的坐标即可：

context.translate(x, y);

为进一步使读者理解，下面举一个例子。首先我们在画布的 (10, 10) 处画出一幅图片：

context.drawImage(img, 10, 10);

然后将 canvas 画布左上角移至 (100, 100) ：

context.translate(100, 100);

此时画布上的图像并没有变换，因为平移的是画布坐标，而不是画布上的图像，即图像并不与坐标一同平移。之后再次在画布的 (10, 10) 处画出一幅图片：

context.drawImage(img, 10, 10);

以上代码执行完毕后的结果如图1-5所示。

图1-5 translate 示例运行结果

translate 所操作的点永远都是画布的左上角，如果希望将执行context.translate(x, y) 后画布的坐标恢复到之前的状态应再执行context.translate(-x, -y) ，画布默认的原点在左上角，水平方向右侧为正方向，垂直方向下侧为正方向，这与我们熟悉的直角坐标系有所不同。

2.2图像缩放

canvas 通过 scale 对图像进行缩放。缩放后的画布的原点与原画布的原点相对应，所以如果希望以图像中心为参考点，缩放前应先将画布原点平移至图像中心。

scale 有两个参数，分别是画布横向的放大倍数和纵向的放大倍数：

context.scale(scalewidth, scaleheight);

比如 context.scale(2, 2) 将画布的横向和纵向均变为原来的2倍，图1-6给出了缩放变换后的结果。

图1-6 缩放变换后的结果

缩放变换是对画布的变换，此操作并不影响已画在画布上的图像，比如如下代码不会改变图像：

context.drawImage(img, 10, 10);
content.scale(2, 2);

正确的方法是缩放图像前应先缩放画布，然后再开始绘图：

content.scale(2, 2);
context.drawImage(img, 10, 10);

scalewidth 和 scaleheight 的绝对值大于1时为放大图像，小于1时为缩小图像，等于1是尺寸与原图像一致。

如前所述，所以如果希望以图像中心为参考点，缩放前应先将画布原点平移至图像中心。比如下列代码以图像中心为参考点，将原图像缩小至原来的1/4（边长缩小至原来的1/2）：

// 先将画布原点移至图像中心，此处图像中心也是画布的中心
content.translate(myCanvas.width/2, myCanvas.height/2);

// 将画布缩小至原画布的1/4
content.scale(0.5, 0.5);

// 将原点还原
content.translate(-myCanvas.width/2, -myCanvas.height/2);

// 将图像画在画布中
context.drawImage(img, 10, 10);

运行结果如图1-7所示。

图1-7 以图像中心为参考点缩放图像

2.3镜像变换

canvas 中并没有为镜像变换专门提供方法，但不必紧张，至此我们依然尚未接触到像素级的操作。在上一节中介绍了图像缩放的相关内容，其中讲到 scalewidth和 scaleheight 的绝对值大于1时为放大，小于1时为缩小，但并没有提到其正负。

通常情况下， scale 的两个参数均是正数，如果为负数，则为镜像效果。比如有如下代码：

content.translate(myCanvas.width/2, myCanvas.height/2);
content.scale(-1, 1);
content.translate(myCanvas.width/2, myCanvas.height/2);
content.drawImage(img, 10, 10);

请注意，在做镜像变换之前一定要先平移画布原点到合适的位置，否则由于画布默认以左上角为原点，镜像变换后的图像会在画布之外导致不可见。

这种以图片垂直中线为对称轴左右镜像的变换叫做水平镜像变换，变换后的结果如图1-8所示。

图1-8 水平镜像变换

另一种变换叫做垂直镜像变换，这种变换以图像的水平中线为对称轴，变换方法为：

content.scale(1, -1);

垂直镜像变换同样需要先平移画布原点，此处代码中不再重复叙述。垂直变换后的结果如图1-9所示。

图1-9 垂直镜像变换

2.4图像旋转

canvas 通过 rotate 方法进行图像旋转操作。 rotate 方法以画布原点作为旋转中心，以弧度作为旋转角度单位，正数代表顺时针旋转。

context.rotate(angle);

如果想要以度作为角度单位，需要使用转换公式 degree*Math.PI/180 ，如以下代码使画布顺时针旋转30°：

context.rotate(30*Math.PI/180);

如果希望以图像中心作为旋转中心，首先需要将画布原点移至图像中心：

context.translate(imgCenterX, imgCenterY);

同样， rotate 只影响画布坐标，不影响已画在画布上的图像。

下列代码以图像中心为旋转中心，将图像顺时针旋转了45°：

context.translate(myCanvas.width/2, myCanvas.height/2);
context.rotate(45*Math.PI/180);
context.translate(-myCanvas.width/2, -myCanvas.height/2);
context.drawImage(img, 10, 10);

旋转后的结果如图1-10所示。

图1-10 利用 rotate 旋转图像

2.5图像转置

图像的转置操作是将图像每行水平排列的像素顺次垂直排列，直观地说就是以图像自左上角至右下角的对角线为对称轴翻转图像 1 。

1 此处说法并不严谨，仅为让读者更易领悟转置的定义，实际上只有正方形的图像转置操作才是以图像自左上角至右下角的对角线为对称轴翻转的。

canvas 没有为图像转置专门提供方法，但我们可以利用旋转和镜像组合的方法实现图像转置的目的。图像的转置可以分解为水平翻转后再顺时针旋转90°，或是垂直翻转后再逆时针旋转90°。下面我们利用顺时针旋转90°后再水平翻转实现图像转置的操作：

context.translate(myCanvas.width/2, myCanvas.height/2);
context.scale(-1, 1);
context.rotate(90*Math.PI/180);
context.translate(-myCanvas.width/2, -myCanvas.height/2);
context.drawImage(img, 10, 10);

转置后的结果如图1-11所示。

图1-11 利用 scale 和 rotate 实现图像的转置

细心的读者可能会发现，转置操作应该是水平翻转后再逆时针旋转90°，但为何此处要顺时针旋转90°却能得到正确的结果呢？原因很简单，因为翻转把画布的坐标轴也翻转了，在原有坐标系下的逆时针旋转在新的坐标系下就变成了顺时针旋转，此处还请读者仔细品味。

另外，如果是先旋转再翻转，则至少需要改变一种操作的变换方向，比如保持顺时针旋转90°的同时，需要进行垂直镜像的操作，而不再是水平镜像操作。下面的代码与上面的代码实现的同样的效果：

context.translate(myCanvas.width/2, myCanvas.height/2);
context.rotate(90*Math.PI/180);
context.scale(1, -1);
context.translate(-myCanvas.width/2, -myCanvas.height/2);
context.drawImage(img, 10, 10);

3.图像傅里叶变换

上一节中我们了解了图像的几何变换，几何变换是空间域中对图像的处理方法，理解起来很容易，处理起来也很形象。在图像处理中还有一种方法是在频域上对图像进行变换，图像的频域变换没有空间域变换直观，理解起来有一定的难度，本节会用最通俗易懂的方式向读者讲解有关频域处理图像的方法，如果读者需要深入了解有关内容，可以参见《Visual C++数字图像处理典型算法及实现》第五章的内容。

3.1图像傅里叶变换的意义

由于图像中红色、绿色和蓝色三个颜色通道是相互独立的，所以可以将一幅彩色图像看成是三张独立的灰度图像，这也是图像处理通常只讨论灰度图像处理方法的原因。同样，下面我们也讲只讨论灰度图像的处理。

对于一幅灰度图像，给出一个图像上像素点的坐标 (x, y) ，我们都可以找到这个像素点的灰度值 z ，于是我们可以将一幅图像抽象成一个函数 z=f(x, y) 。很显然，抽象出来的函数是一个离散型函数，这种抽象思想很重要，它将对图像的处理演变成了对函数的处理，从而使得图像处理这一问题变成了纯粹的数学问题。

由于每一幅图像都唯一地对应一个函数 f(x, y) ，所以这一函数的性质可以反映出所对应图像的性质。傅里叶变换就是把一个离散函数变成无限多个正弦函数的叠加，这些正弦函数的频率体现了离散函数的性质，从而体现图像的性质，这就是图像傅里叶变换的意义。

3.2空间域特性在频域中的表现

虽然图像在频域上比较抽象，但我们依然可以通过对照图像空间域的特性在频域中的表现，来直观感受频率所体现的图像特性。

对于一维函数 y=g(x) ，经过傅里叶变换后，就得到了傅里叶变换的频率谱，此频率谱以傅里叶展开得到的一系列正弦函数的频率为横坐标，对应正弦函数的幅度为纵坐标。对于图像转换来的函数 z=f(x, y) ，是一个二维函数，那么图像傅里叶变换的频率谱就应该是一个三维的图像。

清楚了这一点，我们就可以继续思考了。先来考虑一幅最简单的图像——纯色图像。对于一幅纯色图像，其灰度值处处相等，其转换为函数后为 z=C ，对应的函数图像为与 xOy 面平行的平面，且此平面过点 (0, 0, C) 。显然其傅里叶变换的结果就是函数本身 z=C （频率为0，幅度为C，其他频率分量正弦波的幅度均为0），那么其归一化频率谱就是 (0, 0, 1) 处的一个点，其他位置无图像。

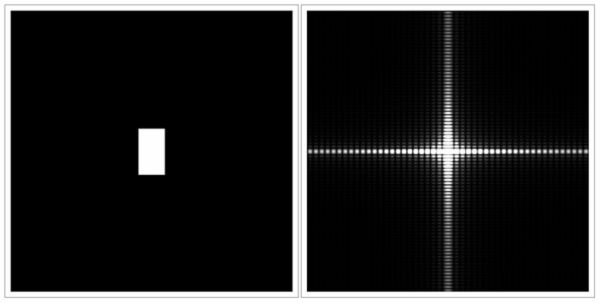
图1-12是同一幅图像分别在空间域和频域上的表现形式。

图1-12 同一幅图像分别在空间域和频域上的表现形式

图中左侧为图像在空间域中像素灰度的分布，这也是正常情况下图像的表现形式。右侧为此图像在频域中的表现形式，图中中心处为坐标原点，所以图像中心代表低频，图像四周代表高频，颜色越白代表能量越高，颜色越黑代表能量越低。值得注意的是，在频谱图像中体现出了负频率（2、3、4象限图像），这只是数学上计算得出的结果，并没有实际的物理意义。

对于一幅图像来说，通常其频谱都是低频能量高，高频能量少，为了找出其中的原因，让我们来探索下频域中的频率到底与空间域中图像的表现形式是如何对应起来的。下面请将图1-13与图1-12对照来看。

图1-13 边缘模糊图像的频率谱

图1-13中的图像是将图1-12经过高斯模糊得到的，可以发现模糊后的图像的频率中高频部分消失了，由此可见，图像频谱高频部分体现了图像中颜色变化明显的特性，这些颜色变化明显的部分在空间域上就对应于图像中图形的边界或者噪点。

下面我们再来将图1-14与图1-12对照来看。

图1-14 灰度动态范围压缩后图像的频率谱

可以看出，如果压缩图像灰度的动态范围，但保留图像的细节，则频率谱表现为低频部分被滤除，由此可见频率谱低频部分描述的是图像平滑区域的灰度动态范围。

除此之外，频率谱还在其它一些特性上与空间域图像有对应关系。空间图像旋转一定角度后，频率谱也相应旋转，如图1-15。

图1-15 图像在空间域中旋转后频率谱也相应旋转

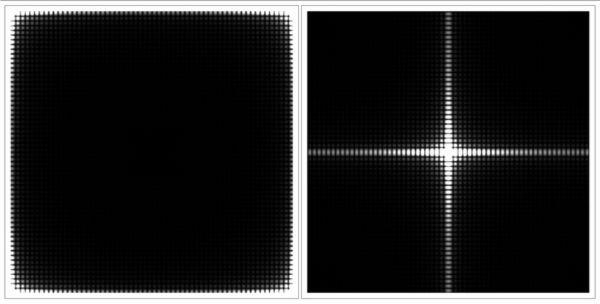
当图像被放大后，图像频率谱的网格会缩小，如图1-16所示。

图1-16 图像被放大后频率谱的网格会缩小

知道这些性质后，图像在频域上抽象的表现形式就变得直观起来了。上面都是简单几何图形的例子，通常自然界中照片的频率谱显得更加复杂和混乱，图1-17展示了自然界中一幅照片的频率谱。

图1-17 自然界中照片的频率谱

3.3快速傅里叶变换

图像有空间域到频域的转换需要进行傅里叶变换，对于离散傅里叶变换的时间复杂度为O(N^2)，如果N比较大，这将是巨大的计算量，从而无法让计算机实时进行处理。快速傅里叶变换完成了离散傅里叶变换所做的工作，并把时间复杂度压缩到O(NlogN)。

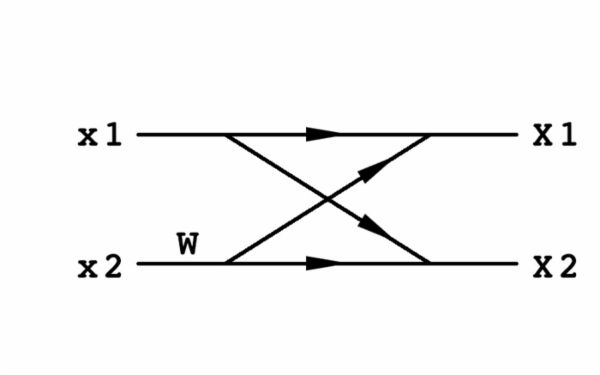
快速傅里叶变换的算法有很多种，目前使用比较广泛的是蝶形算法，蝶形算法是将整个变换的计算过程分解为多个级，每个级又分解为多个组，每个组又包含多个单元。图1-18给出了一个单元的计算过程。

图1-18 蝶形运算中一个单元的计算过程

其中 X1=x1+x2*W ， X2=x1-x2*W 。

图1-19给出了一个长度为8的数组，进行蝶形快速傅里叶变换计算过程的流程图。

图1-19 蝶形快速傅里叶变换计算流程图，图片来自cnx.org

从图中我们可以看出对于长度为8的数组，我们将计算过程分为3个级，自左向右第1级有4个组，每组包含一个计算单元；第2级有2个组，每组包含2个计算单元；第3级有1个组，包含4个计算单元。

为论述与代码保持一致，下面提到的级序数i、组序数j和计算单元序数k的取值均从0开始。对于长度为2^r的数组，进行蝶形快速傅里叶变换计算时分为r个级，第i级有2^(r-i-1)个组，第i级中每个组中包含有2^i个计算单元。

计算单元中的系数W是与级数和计算单元序数有关的，对于第i级中每组的第k个计算单元的系数为Wn[2^(r-1-i)*k]，其中r为计算过程的总级数。

Wn是一个数组，其值与所变换数组的长度有关。对于长度为2^r的数组，Wn的长度为2^(r-1)，Wn[k]=cos(-2π*k/2^r)+sin(-2π*k/2^r)i，其中i为虚数单位。

细心的读者也许会发现，进行蝶形快速傅里叶变换时，左侧数列的位序与右侧最终结果的位序并不相同，所以在进行变换前需要先对原有数列重新排列，我们称之为倒位序排列。下面是JavaScript实现蝶形快速傅里叶算法的完整代码：

function fft(dataArray) {
  // 复数乘法
  this.mul = function(a, b) {
    if(typeof(a)!=='object') {
      a = {real: a, imag: 0}
    }
    if(typeof(b)!=='object') {
      b = {real: b, imag: 0}
    }
    return {
      real: a.real*b.real-a.imag*b.imag,
      imag: a.real*b.imag+a.imag*b.real
    };
  };

  // 复数加法
  this.add = function(a, b) {
    if(typeof(a)!=='object') {
      a = {real: a, imag: 0}
    }
    if(typeof(b)!=='object') {
      b = {real: b, imag: 0}
    }
    return {
      real: a.real+b.real,
      imag: a.imag+b.imag
    };
  };

  // 复数减法
  this.sub = function(a, b) {
    if(typeof(a)!=='object') {
      a = {real: a, imag: 0}
    }
    if(typeof(b)!=='object') {
      b = {real: b, imag: 0}
    }
    return {
      real: a.real-b.real,
      imag: a.imag-b.imag
    };
  };

  // 倒位序排列
  this.sort = function(data, r) {
    if(data.length <=2) {
      return data;
    }
    var index = [0,1];
    for(var i=0; i1; i++) {
      var tempIndex = [];
      for(var j=0; j        tempIndex[j] = index[j]*2;
        tempIndex[j+index.length] = index[j]*2+1;
      }
      index = tempIndex;
    }
    var datatemp = [];
    for(var i=0; i      datatemp.push(data[index[i]]);
    }
    return datatemp;
  };

  var dataLen = dataArray.length;
  var r = 1; // 迭代次数
  var i = 1;
  while(i*2 < dataLen) {
    i *= 2;
    r++;
  }
  var count = 1<<r; // 相当于count=2^r

  // 如果数据dataArray的长度不是2^N，则开始补0
  for(var i=dataLen; i<count; i++) {
    dataArray[i] = 0;
  }

  // 倒位序处理
  dataArray = this.sort(dataArray, r);

  // 计算加权系数w
  var w = [];
  for(var i=0; i<count/2; i++) {
    var angle = -i*Math.PI*2/count;
    w.push({real: Math.cos(angle), imag: Math.sin(angle)});
  }

  for(var i=0; i<r; i++) { // 级循环
    var group = 1<<(r-1-i);
    var distance = 1<<i;
    var unit = 1<<i;
    for(var j=0; j<group; j++) { // 组循环
      var step = 2*distance*j;
      for(var k=0; k<unit; k++) { // 计算单元循环
        var temp = this.mul(dataArray[step+k+distance], w[count*k/2/distance]);
        dataArray[step+k+distance] = this.sub(dataArray[step+k], temp);
        dataArray[step+k] = this.add(dataArray[step+k], temp);
      }
    }
  }
  return dataArray;
}

上面是一维快速傅里叶的算法，快速傅里叶变换的逆变换用JavaScript实现的完整代码如下：

function ifft(dataArray) {
  for(var i=0, dataLen=dataArray.length; i<dataLen; i++) {
    if(typeof(dataArray[i])!='object'){
      dataArray[i] = {
        real: dataArray[i],
        imag: 0
      }
    }
    dataArray[i].imag *= -1;
  }
  dataArray = fft(dataArray);
  for(var i=0, dataLen=dataArray.length; i<dataLen; i++) {
    dataArray[i].real *= 1/dataLen;
    dataArray[i].imag *= -1/dataLen;
  }
  return dataArray;
}

由于灰度图像是一个二维数组，所以我们需要用到二维傅里叶变换。二维傅里叶变换可以通过一维傅里叶变换得到，首先对二维数组的每一行进行一维傅里叶变换，并用变换后的结果代替原有的数据，然后再对经过行变换后的二维数组的每一列进行一维傅里叶变换，并用变换后的结果代替原有的数据。下面是JavaScript实现二维傅里叶变换的完整代码：

function fft2(dataArray, width, height) {
  var r = 1;
  var i = 1;
  while(i*2 < width) {
    i *= 2;
    r++;
  }
  var width2 = 1<<r;
 var r = 1;
  var i = 1;
  while(i*2 < height) {
    i *= 2;
    r++;
  }
  var height2 = 1<<r;

  var dataArrayTemp = [];
  for(var i=0; i<height2; i++) {
    for(var j=0; j<width2; j++) {
      if(i>=height || j>=width) {
        dataArrayTemp.push(0);
      }
      else {
        dataArrayTemp.push(dataArray[i*width+j]);
      }
    }
  }

  dataArray = dataArrayTemp;
  width = width2;
  height = height2;

  var dataTemp = [];
  var dataArray2 = [];
  for(var i=0; i<height; i++) {
    dataTemp = [];
    for(var j=0; j<width; j++) {
      dataTemp.push(dataArray[i*width+j]);
    }
    dataTemp = fft(dataTemp);
    for(var j=0; j<width; j++) {
      dataArray2.push(dataTemp[j]);
    }
  }
  dataArray = dataArray2;
  dataArray2 = [];
  for(var i=0; i<width; i++) {
    var dataTemp = [];
    for(var j=0; j<height; j++) {
      dataTemp.push(dataArray[j*width+i]);
    }
    dataTemp = fft(dataTemp);
    for(var j=0; j<height; j++) {
      dataArray2.push(dataTemp[j]);
    }
  }
  dataArray = [];
  for(var i=0; i<height; i++) {
    for(var j=0; j<width; j++) {
      dataArray[j*height+i] = dataArray2[i*width+j];
    }
  }
  return dataArray;
}

图像经过二维傅里叶变换所得到的结果就是前面提到的频率谱。需要注意的一点是，由于图像像素的排列是自左向右自上向下的，即图像的坐标原点在左上角，且纵向正方向向下，这导致变换后得到的频谱与前面有所不同——低频出现在图像四周，高频出现在图像中心。如图1-20左侧所示，左侧是直接转换后得到的频谱，右侧是将原点移至中心的频谱。

图1-20 未经处理的频谱高频在图像中心

4.图像增强

图像增强包括图像的平滑处理、去噪点、寻找边缘和图像锐化等。处理的方法有两种，一种是在空间域中对图像的灰度值重新计算，另一种是先将图像转换到频域上，对图像的频谱进行运算，然后再利用逆变换将图像还原到空间域中。本节将从空间域和频域两种处理方法讲解图像增强有关的内容。

4.1卷积运算

卷积运算是空间域中处理图像最常用的计算方法，比如模板运算（mask）就是一种卷积运算。对于连续函数 f(x) 和 g(x) ，其卷积运算所得的新的函数 F(x) 有如下定义：

F(x)=f*g=\int_{-\infty}^{\infty} f(x).g(t-x)\, dt

对于离散函数 f(x) 和 g(x) ，其卷积定义为：

F(x)=f*g=\sum_t f(x).g(t-x)

扩展到二维离散函数 I(x, y) 和 G(x, y) 的卷积，有定义：

I_{\sigma}(x,y)=I*G=\sum_i \sum_j I(x,y).G(i-x,j-y)

如果有

G(x,y)=\frac{1}{2\pi\rho^2}e^{-(x^2+y^2)/2\rho^2}

则上式的操作就变成了高斯模糊处理。

但在实际操作中，我们往往并不是在整个图像空间域中做卷积运算，因为那样计算量是非常巨大的。比如对于一个100*100的图像如果在整个空间域做卷积，需要进行1亿次乘法和1亿次加法，这是不可接受的。为了使计算机可以实时处理图像，通常只在一个给定的窗口中做卷积运算，而不是整个空间域。常用的窗口有3*3、5*5和7*7等。如果使用3*3的窗口处理100*100的图像则只需进行9万次乘法和9万次加法，大大提高了图像的处理速度。

4.2模板运算

模板运算可以简单看成是模板与窗口中像素的对乘加，比如有模板：

\frac{1}{9}\begin{bmatrix}1&1&1\\1&1&1\\1&1&1\end{bmatrix}

和窗口像素：

\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}

则窗口中心像素灰度值经计算后将变为 \frac{a+b+c+d+e+f+g+h+i}{9} ，实际就是用一个像素周围的8个像素点，和其自身灰度值的均值，代替原有的灰度值，最后的结果就是图像变得更加平滑，但是边缘也会显得更加模糊，如图1-21所示。

图1-21 使用模板使图像变得模糊

如果模板为：

\begin{bmatrix}0&1&0\\1&-4&1\\0&1&0\end{bmatrix}

在实现的效果为边缘检测，如图1-22所示。

图1-22 使用模板进行边缘检测

利用JavaScript实现模板运算的完整算法如下：

function mask(maskArray, dataArray, width, height) {
  var maskWidth = maskArray.length;
  var maskHeight = maskArray[0].length;
  var xStart = (maskWidth-1)/2;
  var xEnd = width-xStart;
  var yStart = (maskHeight-1)/2;
  var yEnd = height-yStart;
  var maskXStart = -(maskWidth-1)/2;
  var maskXEnd = -maskXStart;
  var maskYStart = -(maskHeight-1)/2;
  var maskYEnd = -maskYStart;
  var temp=[],tempSum,x,y,i,j,tempMaskArray,index=0;
  for(y=0; y    for(x=0; x      if(x>xStart && xyStart && y        tempSum  = 0;
        for(j=maskYStart; j<=maskYEnd; j++) {
          tempMaskArray = maskArray[j-maskYStart];
          for(i=maskXStart; i<=maskXEnd; i++) {
            tempSum += dataArray[(j+y)*width+i+x]*
                tempMaskArray[i-maskXStart];
          }
        }
        temp[index] = Math.round(tempSum);
      }
      else {
        temp[index] = dataArray[index];
      }
      index++;
    }
  }
  return temp;
}

4.3中值滤波

中值滤波不再是像模板运算那样计算加权平均值，其思想是用窗口像素灰度值的中间值代替相应像素点的灰度值。中值滤波的好处是使图像变得平滑的同时，保留了像素点直接灰度值的梯度。

利用JavaScript实现中值滤波的完整代码如下：

function median(filterWidth, filterHeight, dataArray, width, height) {
  var temp = [];
  for(var i=0; i    temp.push(dataArray[i]);
  }
  for(var x=(filterWidth-1)/2; x1)/2; x++) {
    for(var y=(filterHeight-1)/2; y1)/2; y++) {
      var tempArray = [];
      for(var i=-(filterWidth-1)/2; i<=(filterWidth-1)/2; i++) {
        for(var j=-(filterHeight-1)/2; j<=(filterHeight-1)/2; j++) {
          tempArray.push(temp[(j+y)*width+i+x]);
        }
      }
      // 泡沫排序，找出中值
      do {
        var loop = 0;
        for(var i=0; i1; i++) {
          if(tempArray[i]>tempArray[i+1]) {
            var tempChange = tempArray[i];
            tempArray[i] = tempArray[i+1];
            tempArray[i+1] = tempChange;
            loop = 1;
          }
        }
      }while(loop);
      dataArray[y*width+x] = tempArray[Math.round(tempArray.length/2)];
    }
  }
  return dataArray;
}

图1-23是通过中值滤波去除图像噪点的结果。

图1-23 利用中值滤波去除图像噪点

4.4频域图像增强

频域图像增强的思想是先将图像转换到频域，通过转移函数H得到新的图像频谱，最后再转换到空间域：

I => F => F*H => I'

对于不同的转移函数H，可以得到不同的增强效果。低通滤波器可以使图像变得更加平滑，常见的低通滤波器有巴特沃斯低通滤波器和梯形低通滤波器。n阶巴特沃斯低通滤波器对应的转换函数为 H(u,v)=\frac{1}{1+{[D_0/D(u,v)]}^{2n}} ，其中D(u, v) 为点 (u, v) 到频域原点的距离。图1-24为1阶巴特沃兹低通滤波器处理图像的结果， D_0 取图片宽度的1/16。

图1-24 巴特沃兹低通滤波器处理图像

高通滤波器保留图像的高频部分而滤除了低频部分，巴特沃斯高通滤波器是一种常见的高通滤波器，n阶巴特沃斯高通滤波器对应的转换函数为 H(u,v)=\frac{1}{1+{[D(u,v)/D_0]}^{2n}} ，其中 D(u, v) 为点 (u, v) 到频域原点的距离。图1-25为1阶巴特沃兹高通滤波器处理图像的结果， D_0 取图片宽度的1/16。

图1-25 巴特沃兹高通滤波器处理图像

写得超详细，很有帮助。

转自：http://www.ituring.com.cn/article/121428