32.算法图解(python)1-7
https://pan.baidu.com/s/1pmMGoEcQspYUNc_2hmWUEg
讲解了概念,有例题,有答案,代码不算多。非常好的入门级书。图灵的书是真不错
广度优先搜索、狄克斯特拉算法、贪婪算法、动态规划、K最近邻算法、
常用算法https://blog.csdn.net/dQCFKyQDXYm3F8rB0/article/details/89077881
第一章:算法简介
二分查找的速度比简单查找快得多。
O(log n)比O(n)快。需要搜索的元素越多,前者比后者就快得越多。 算法运行时间并不以秒为单位。
算法运行时间是从其增速的角度度量的。
算法运行时间用大O表示法表示。
1.1 假设有一个包含128个名字的有序列表,你要使用二分查找在其中查找一个名字,请 问最多需要几步才能找到?
7步
1.2 上面列表的长度翻倍后,最多需要几步
8步
使用大O表示法给出下述各种情形的运行时间。
1.3 在电话簿中根据名字查找电话号码。
我的答案:O(1) 书的答案:O(log n)
1.4 在电话簿中根据电话号码找人。(提示:你必须查找整个电话簿。)
O(n)
1.5 阅读电话簿中每个人的电话号码。
O(n)
1.6 阅读电话簿中姓名以A打头的人的电话号码。这个问题比较棘手,它涉及第4章的概 念。答案可能让你感到惊讶!
我的答案:O(1) 书的答案:O(n)。你可能认为,我只对26个字母中的一个这样做,因此运行时间应为O(n / 26)。需要 牢记的一条简单规则是,大O表示法不考虑乘以、除以、加上或减去的数字。下面这些 都不是正确的大O运行时间:O(n + 26)、O(n 26)、O(n * 26)、O(n / 26),它们都应表示 为O(n)!为什么呢?如果你好奇,请翻到4.3节,并研究大O表示法中的常量(常量就是 一个数字,这里的26就是常量)。
def binary_search(list, item):
low = 0
high = len(list) - 1
while low <=high:
mid_index = int((low + high)/2)
mid = list[mid_index]
if mid > item:
high = mid_index - 1
elif mid < item:
low = mid_index + 1
else:
return mid
sorted_list = [1,2,3,4,5,6,7,8,9,22,33,44,55]
print(binary_search(sorted_list, 5))
第2章 选择排序
计算机内存犹如一大堆抽屉。
需要存储多个元素时,可使用数组或链表。
数组的元素都在一起。
链表的元素是分开的,其中每个元素都存储了下一个元素的地址。
数组的读取速度很快。
链表的插入和删除速度很快。
在同一个数组中,所有元素的类型都必须相同(都为int、double等)。
?2.1 假设你要编写一个记账的应用程序。
你每天都将所有的支出记录下来,并在月底统计支出,算算当月花了多少钱。因此, 你执行的插入操作很多,但读取操作很少。该使用数组还是链表呢?
我的答案:链表
书的答案:在这里,你每天都在列表中添加支出项,但每月只读取支出一次。数组的读取速度快, 而插入速度慢;链表的读取速度慢,而插入速度快。由于你执行的插入操作比读取操作 多,因此使用链表更合适。另外,仅当你要随机访问元素时,链表的读取速度才慢。鉴 于你要读取所有的元素,在这种情况下,链表的读取速度也不慢。因此,对这个问题来 说,使用链表是不错的解决方案。
?2.2 假设你要为饭店创建一个接受顾客点菜单的应用程序。这个应用程序存储一系列点菜 单。服务员添加点菜单,而厨师取出点菜单并制作菜肴。这是一个点菜单队列:服务 员在队尾添加点菜单,厨师取出队列开头的点菜单并制作菜肴。
你使用数组还是链表来实现这个队列呢?(提示:链表擅长插入和删除,而数组擅长 随机访问。在这个应用程序中,你要执行的是哪些操作呢?)
链表,弹出首个的,插入末尾。
?2.3 我们来做一个思考实验。假设Facebook记录一系列用户名,每当有用户试图登录 Facebook时,都查找其用户名,如果找到就允许用户登录。由于经常有用户登录 Facebook,因此需要执行大量的用户名查找操作。假设Facebook使用二分查找算法, 而这种算法要求能够随机访问——立即获取中间的用户名。考虑到这一点,应使用数 组还是链表来存储用户名呢?
我的答案:数组 标准答案:有序数组。数组让你能够随机访问——立即获取数组中间的元素,而使用链表无法这
样做。要获取链表中间的元素,你必须从第一个元素开始,沿链接逐渐找到这个元素。
?2.4 经常有用户在Facebook注册。假设你已决定使用数组来存储用户名,在插入方面数组 有何缺点呢?具体地说,在数组中添加新用户将出现什么情况?
我的答案:数组的元素都在一起,为了要插入新的数据,数组要预留很大空间,如果空间不足要移动整个数组到新的空间。可能预留空间不足要移动整个数组到新的空间。
标准答案:数组的插入速度很慢。另外,要使用二分查找算法来查找用户名,数组必须是有序的。 假设有一个名为Adit B的用户在Facebook注册,其用户名将插入到数组末尾,因此每次 插入用户名后,你都必须对数组进行排序!
?2.5 实际上,Facebook存储用户信息时使用的既不是数组也不是链表。假设Facebook使用 的是一种混合数据:链表数组。这个数组包含26个元素,每个元素都指向一个链表。 例如,该数组的第一个元素指向的链表包含所有以A打头的用户名,第二个元素指向的 链表包含所有以B打头的用户名,以此类推。 假设Adit B在Facebook注册,而你需要将其加入前述数据结构中。因此,你访问数组的 第一个元素,再访问该元素指向的链表,并将Adit B添加到这个链表末尾。现在假设你要查找Zakhir H。因此你访问第26个元素,再在它指向的链表(该链表包含所有以z打头的用户名)中查找Zakhir H。 请问,相比于数组和链表,这种混合数据结构的查找和插入速度更慢还是更快?你不必给出大O运行时间,只需指出这种新数据结构的查找和插入速度更快还是更慢。
我的答案:比数组和链表插入慢,比数组查找慢,比链表查找快。
书的答案:查找时,其速度比数组慢,但比链表快;而插入时,其速度比数组快,但与链表相当。 因此,其查找速度比数组慢,但在各方面都不比链表慢。本书后面将介绍另一种混合 数据结构——散列表。这个练习应该能让你对如何使用简单数据结构创建复杂的数据 结构有大致了解。
Facebook实际使用的是什么呢?很可能是十多个数据库,它们基于众多不同的数据结 构:散列表、B树等。数组和链表是这些更复杂的数据结构的基石。
def find_smallest(lis):
smallest = lis[0]
smallest_index = 0
for i in range(1,len(lis)):
if smallest > lis[i]:
smallest = lis[i]
smallest_index = i
return smallest_index
def selection_sort(lis):
new_lis = []
for i in range(len(lis)):
smallest_index = find_smallest(lis)
new_lis.append(lis.pop(smallest_index))
return new_lis
disorder_list = [2,3,1,3,4,5,55,22,33,11,9]
print(selection_sort(disorder_list))
第3章 递归:
递归指的是调用自己的函数。
每个递归函数都有两个条件:基线条件和递归条件。 栈有两种操作:压入和弹出。
所有函数调用都进入调用栈。
调用栈可能很长,这将占用大量的内存。
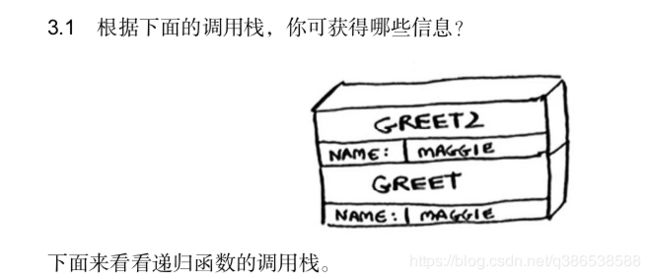
我的答案:两个函数greet和greet2;函数变量name的值是maggie
书的答案:
首先调用了函数greet,并将参数name的值指定为maggie。
接下来,函数greet调用了函数greet2,并将参数name的值指定为maggie。 此时函数greet处于未完成(挂起)状态。
当前的函数调用为函数greet2。
这个函数执行完毕后,函数greet将接着执行。
3.2 假设你编写了一个递归函数,但不小心导致它没完没了地运行。正如你看到的,对于 每次函数调用,计算机都将为其在栈中分配内存。 递归函数没完没了地运行时,将给 栈带来什么影响?
我的答案:栈的空间堆满了,之前的数据被后面的数据取代
书的答案:栈将不断地增大。每个程序可使用的调用栈空间都有限,程序用完这些空间(终将如 此)后,将因栈溢出而终止。
def factorial(n):
if isinstance(n,int) and n >=0:
if n == 1 or n == 0:
return 1
else:
return n * factory(n - 1)
else:
return "请输入自然数"
第四章:快速排序
D&C将问题逐步分解。使用D&C处理列表时,基线条件很可能是空数组或只包含一个元 素的数组。
实现快速排序时,请随机地选择用作基准值的元素。快速排序的平均运行时间为O(n log n)。
大O表示法中的常量有时候事关重大,这就是快速排序比合并排序快的原因所在。
比较简单查找和二分查找时,常量几乎无关紧要,因为列表很长时,O(log n)的速度比O(n)
快得多。
4.1 请编写前述sum函数的代码。
我的答案:
def sum_factorial(arr):
if len(arr) == 1:
return arr.pop()
else:
return arr.pop() + sum_factorial(arr)
sorted_list = [1,2,3,4,5,6,7,8,9,10]
print(sum_factorial(sorted_list))
书的答案:
def sum(list):
if list == []:
return 0
return list[0] + sum(list[1:])
4.2 编写一个递归函数来计算列表包含的元素数。
书的答案:
defcount(list): if list == []:
return 0
return 1 + count(list[1:])
4.3 找出列表中最大的数字。
我的答案:
def find_max(lis):
max = lis[0]
max_index = 0
for i in range(1,len(lis)-1):
if max < lis[i]:
max = lis[i]
max_index = i
return max
disorder_list = [2,3,1,3,4,5,55,22,33,11,9]
print(find_max(disorder_list))
书的答案:
def max(list):
if len(list) == 2:
return list[0] if list[0] > list[1] else list[1]
sub_max = max(list[1:])
return list[0] if list[0] > sub_max else sub_max
sorted_list = [1,2,3,4,5,6,7,8,9,10]
print(max(sorted_list))
4.4 还记得第1章介绍的二分查找吗?它也是一种分而治之算法。你能 9 找出二分查找算法的基线条件和递归条件吗?
我的答案:基线条件:中间值等于要找的值
递归条件: 数组长度为1
书的答案:
二分查找的基线条件是数组只包含一个元素。如果要查找的值与这个元素相同,就找
到了!否则,就说明它不在数组中。
在二分查找的递归条件中,你把数组分成两半,将其中一半丢弃,并对另一半执行二 分查找。
使用大O表示法时,下面各种操作都需要多长时间?
4.5 打印数组中每个元素的值。
O(n)
4.6 将数组中每个元素的值都乘以2。
O(n)
4.7 只将数组中第一个元素的值乘以2。
O(1)
4.8 根据数组包含的元素创建一个乘法表,即如果数组为[2, 3, 7, 8, 10],首先将每个元素
都乘以2,再将每个元素都乘以3,然后将每个元素都乘以7,以此类推。
O(n^2)
第5章散列表
散列表适合用于:
模拟映射关系;
防止重复;
缓存/记住数据,以免服务器再通过处理来生成它们
你可以结合散列函数和数组来创建散列表。
冲突很糟糕,你应使用可以最大限度减少冲突的散列函数。 散列表的查找、插入和删除速度都非常快。
散列表适合用于模拟映射关系。
一旦填装因子超过0.7,就该调整散列表的长度。
散列表可用于缓存数据(例如,在Web服务器上)。
散列表非常适合用于防止重复。
练习
对于同样的输入,散列表必须返回同样的输出,这一点很重要。如果不是这样的,就无法找到你在散列表中添加的元素!
请问下面哪些散列函数是一致的?
5.1 f(x)=1 无论输入是什么,都返回1
5.2 f(x)=rand()
5.3 f(x)=next_empty_slot()
5.4 f(x)=len(x) 将字符串的长度用作索引
5.1和5.4
散列函数的结果必须是均匀分布的,这很重要。它们的映射范围必须尽可能大。最糟糕的散 列函数莫过于将所有输入都映射到散列表的同一个位置。 假设你有四个处理字符串的散列函数。
A. 不管输入是什么,都返回1。
B. 将字符串的长度用作索引。
C. 将字符串的第一个字符用作索引。即将所有以a打头的字符串都映射到散列表的同一个位 置,以此类推。
D. 将每个字符都映射到一个素数:a = 2,b = 3,c = 5,d = 7,e = 11,等等。对于给定的字 符串,这个散列函数将其中每个字符对应的素数相加,再计算结果除以散列表长度的余数。
例如,如果散列表的长度为10,字符串为bag,则索引为(3 + 2 + 17) % 10 = 22 % 10 = 2。
在下面的每个示例中,上述哪个散列函数可实现均匀分布?假设散列表的长度为10。
5.5 将姓名和电话号码分别作为键和值的电话簿,其中联系人姓名为Esther、Ben、Bob和 Dan。
我的答案:D
书的答案:c、d
5.6 电池尺寸到功率的映射,其中电池尺寸为A、AA、AAA和AAAA。
B、D
5.7 书名到作者的映射,其中书名分别为Maus、Fun Home和Watchmen。
B、C、D
box_ = {}
def box(item):
if box_.get(item):
print("已经有%s" %item)
else:
box_[item] = True
print("没有%s" %item)
box('打火机')
box('打火机')
第六章 广度优先搜索:
广度优先搜索指出是否有从A到B的路径。
如果有,广度优先搜索将找出最短路径。
面临类似于寻找最短路径的问题时,可尝试使用图来建立模型,再使用广度优先搜索来
解决问题。
有向图中的边为箭头,箭头的方向指定了关系的方向,例如,rama→adit表示rama欠adit钱。
无向图中的边不带箭头,其中的关系是双向的,例如,ross - rachel表示“ross与rachel约
会,而rachel也与ross约会”。
队列是先进先出(FIFO)的。
栈是后进先出(LIFO)的。
你需要按加入顺序检查搜索列表中的人,否则找到的就不是最短路径,因此搜索列表必
须是队列。
对于检查过的人,务必不要再去检查,否则可能导致无限循环。
练习
对于下面的每个图,使用广度优先搜索算法来找出答案。
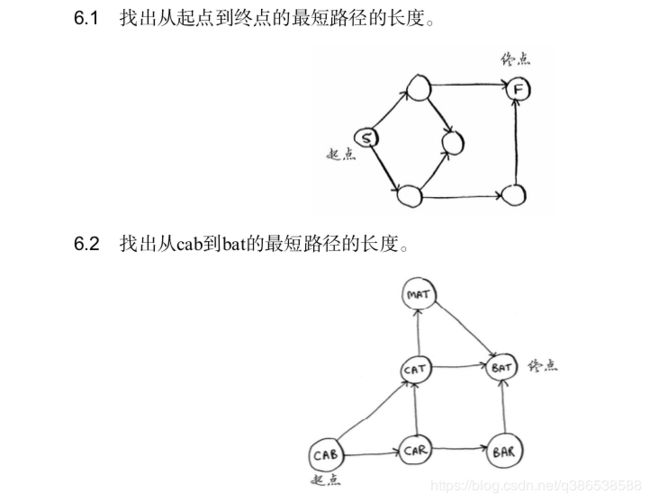
6.1和6.2:2步和2步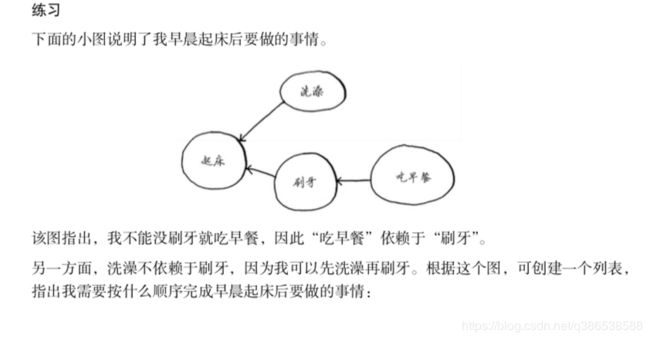 (1) 起床
(1) 起床
(2) 洗澡
(3) 刷牙
(4) 吃早餐 请注意,“洗澡”可随便移动,因此下面的列表也可行: (1) 起床
(2) 刷牙
(3) 洗澡
(4) 吃早餐
6.3 请问下面的三个列表哪些可行、哪些不可行?

只有b可行
6.4 下面是一个更大的图,请根据它创建一个可行的列表。 从某种程度上说,这种列表是有序的。如果任务A依赖于任务B,在列表中任务A就必须在任 务B后面。这被称为拓扑排序,使用它可根据图创建一个有序列表。假设你正在规划一场婚 礼,并有一个很大的图,其中充斥着需要做的事情,但却不知道要从哪里开始。这时就可使 用拓扑排序来创建一个有序的任务列表。树是一种特殊的图,其中没有往后指的边。
从某种程度上说,这种列表是有序的。如果任务A依赖于任务B,在列表中任务A就必须在任 务B后面。这被称为拓扑排序,使用它可根据图创建一个有序列表。假设你正在规划一场婚 礼,并有一个很大的图,其中充斥着需要做的事情,但却不知道要从哪里开始。这时就可使 用拓扑排序来创建一个有序的任务列表。树是一种特殊的图,其中没有往后指的边。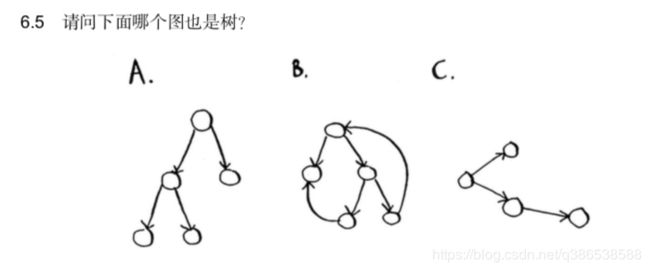 a和c
a和c
from collections import deque
def person_is_seller(person):
return person == 'jonny'
graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []
search_queue = deque()
search_queue = graph["you"]
def breadth_first_search(search_queue):
searched = []
while search_queue:
person = search_queue.pop()
if person not in searched:
searched.append(person)
if person_is_seller(person):
print("%s is seller" %person)
return True
else:
search_queue += graph[person]
return False
breadth_first_search(search_queue)