winograd卷积的实现——ncnn的x86版本的一点心得
winograd卷积?
论文题目:Fast Algorithms for Convolutional Neural Networks
链接传送:https://arxiv.org/abs/1509.09308v2
请读者看过论文再往下看,这论文真的不难懂。下面的内容假设读者已经阅读过论文。
核心公式
Y = A T [ U ⊙ V ] A Y=A^T[U\odot V]A Y=AT[U⊙V]A
其中, U = G g G T U=GgG^T U=GgGT, V = B T d B V=B^TdB V=BTdB, G G G、 B B B、 A A A都是常系数矩阵, g g g是卷积核, d d d是输入, ⊙ \odot ⊙代表点乘。详细的解释论文里都有,相信大家都了解了。整个算法最核心的就是上面这个公式,怎么推导的我们就不管了,理解计算细节即可。
核心算法
再啰嗦一下,就算是提点一下主要内容了。论文里面给出了 F ( 2 × 2 , 3 × 3 ) F(2\times2,3\times3) F(2×2,3×3)和 F ( 4 × 4 , 3 × 3 ) F(4\times4,3\times3) F(4×4,3×3)的系数矩阵,当然这些只能算出小块输入的结果,我们不可能根据特征图的大小去推导系数矩阵(大块输入也并不一定效率)。所以,我们就用已知的小块系数矩阵做滑窗,每一次滑窗计算都是按照核心公式算的,具体的算法步骤也就是论文中的表1了。需要说明的是,虽然看起来很多矩阵运算,但这只是论文为了表达清楚才这么写的,有助于我们理解。
ncnn中的实现——x86版本
最近是在看ncnn的代码,水平有限,下面拿x86版本开个刀(就这我还看了好长时间)。
我们主要肢解两个函数,它们位于convolution_x86.cpp的引用的头文件convolution_3x3.h中(说明一下,我是拿cmake生成VS2015工程,然后在名字叫ncnn的解决方案中打开来看的):
static void conv3x3s1_winograd43_transform_kernel_sse(const Mat& kernel, std::vector<Mat> &kernel_tm2, int inch, int outch);
static void conv3x3s1_winograd43_sse(const Mat& bottom_blob, Mat& top_blob, const std::vector<Mat> &kernel_tm_test, const Mat& _bias, const Option& opt);
从名字上来看就能猜到,第一个函数是做权重核变换的,也就是计算上面的核心公式中的 U U U。第二个函数就是算在每次forward的时候计算 V V V和其余运算。
内存排列
我第一次看代码的时候,有点懵逼,全是for循环里面展开操作,代码显得很长,看起来简洁却一点也不简单。不吹牛逼,第一个函数上面一小部分一下就能看懂,就是按着论文公式在算 U U U。但是后面还有好长一段,起初我是完全懵逼的,也没谁给我解释,慢慢摸索了一段时间才看明白。其实主要就是理解作者的内存布局,就能看懂代码。作者当然是先设计好了然后写的代码,我们反过来看,如果没啥经验看着肯定累。我就属于没啥经验的。。好废话说了很多了,下面讲讲内存布局吧,其实也很简单。。就是会了不难,不会的时候怎么也看不懂。。好了,真的开始了。。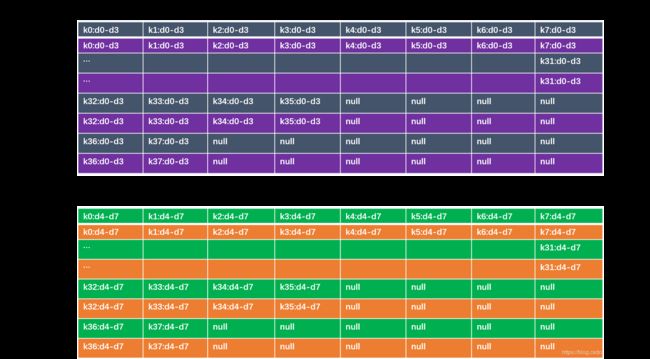
上面这张图是U矩阵的内存布局,我解释一下。我们看的代码是按 F ( 4 × 4 , 3 × 3 ) F(4\times4,3\times3) F(4×4,3×3)来算的,也就是说对应的输入块大小为 6 × 6 6\times6 6×6,一共36个元素,一个块称为一个tile,即一个tile的U矩阵也是 6 × 6 6\times6 6×6,36个元素。在代码中,首先是把U矩阵分成了9段,Kernel_tm_test[0-8],每一段4个数,就像上面两个表一样,每个表表示每一段。每一段的排列又是这样的:首先将卷积核(因为U矩阵是卷积核的变换,是对应的,所以我就称为卷积核了)个数按8个一组分,有余数的再按4个4组分,最后不满4个的落单。这样每个表的宽度是32个数,高度是输入特征图的通道数(表中重复出现的c0 c1,代表输入特征2个通道),通道数是卷积核的个数(上面例子中是c0 c1 c2 c3 总共4个)。
加了点注释的代码
其实知道了U矩阵的内存排列,代码基本上都能看懂了。还有一个要注意的地方,在论文中我们算V矩阵的时候是这么算的:
V = B T d B V=B^TdB V=BTdB上面也已经提到过了,但ncnn用了一个巧妙的方法,避免既要输入 B B B又要输入 B T B^T BT,那就是变形一下核心公式:
Y = A T ( A T ( U ⊙ V T ) ) T Y=A^T(A^T(U\odot V^T))^T Y=AT(AT(U⊙VT))T
这样变换之后,全程只有 A T A^T AT和 B T B^T BT,因为 V T = B T ( B T d ) T V^T=B^T(B^Td)^T VT=BT(BTd)T,我也是被大神深深的折服了。一开始我也不知道作者用了这种方式计算,还很好奇为什么会出现这两行代码(因为h对应的原本是row,w对应的是col),后来才知道转置了。好啦,这次分享就差不多到这了,我贴上去掉了AVX、SSE指令的代码,加了点注释,方便大家对照着理解阅读。等我再学一波,继续分享一下心得。
int nColBlocks = h_tm/6; // may be the block num in Feathercnn
int nRowBlocks = w_tm/6;
static void conv3x3s1_winograd43_transform_kernel_sse(const Mat& kernel, std::vector<Mat> &kernel_tm2, int inch, int outch)
{
Mat kernel_tm(6*6, inch, outch);
// G
const float ktm[6][3] = {
{ 1.0f/4, 0.0f, 0.0f},
{ -1.0f/6, -1.0f/6, -1.0f/6},
{ -1.0f/6, 1.0f/6, -1.0f/6},
{ 1.0f/24, 1.0f/12, 1.0f/6},
{ 1.0f/24, -1.0f/12, 1.0f/6},
{ 0.0f, 0.0f, 1.0f}
};
#pragma omp parallel for
for (int p = 0; p<outch; p++) //k个核
{
for (int q = 0; q<inch; q++) //输入c个通道
{
const float* kernel0 = (const float*)kernel + p*inch * 9 + q * 9;
float* kernel_tm0 = kernel_tm.channel(p).row(q); //Uk,c 6x6
// transform kernel
const float* k0 = kernel0;
const float* k1 = kernel0 + 3;
const float* k2 = kernel0 + 6;
// h
float tmp[6][3]; //这个存的G g_k,c
for (int i=0; i<6; i++)
{
tmp[i][0] = k0[0] * ktm[i][0] + k0[1] * ktm[i][1] + k0[2] * ktm[i][2]; //目测kernel 按列存储
tmp[i][1] = k1[0] * ktm[i][0] + k1[1] * ktm[i][1] + k1[2] * ktm[i][2];
tmp[i][2] = k2[0] * ktm[i][0] + k2[1] * ktm[i][1] + k2[2] * ktm[i][2];
}
// U
for (int j=0; j<6; j++)
{
float* tmpp = &tmp[j][0];
for (int i=0; i<6; i++)
{
kernel_tm0[j*6 + i] = tmpp[0] * ktm[i][0] + tmpp[1] * ktm[i][1] + tmpp[2] * ktm[i][2]; // 乘上G^T,正好乘行
}
}
}
}
//重排U_k,c
for (int r=0; r<9; r++)
{
Mat kernel_tm_test(4*8, inch, outch/8 + (outch%8)/4 + outch%4); //每行8个核,4个数一组,
int p = 0;
for (; p+7<outch; p+=8) //每次8个核
{
const float* kernel0 = (const float*)kernel_tm.channel(p);
const float* kernel1 = (const float*)kernel_tm.channel(p+1);
const float* kernel2 = (const float*)kernel_tm.channel(p+2);
const float* kernel3 = (const float*)kernel_tm.channel(p+3);
const float* kernel4 = (const float*)kernel_tm.channel(p+4);
const float* kernel5 = (const float*)kernel_tm.channel(p+5);
const float* kernel6 = (const float*)kernel_tm.channel(p+6);
const float* kernel7 = (const float*)kernel_tm.channel(p+7);
float* ktmp = kernel_tm_test.channel(p/8);
for (int q=0; q<inch; q++) //输入特征图,通道
{
ktmp[0] = kernel0[r*4+0];
ktmp[1] = kernel0[r*4+1];
ktmp[2] = kernel0[r*4+2];
ktmp[3] = kernel0[r*4+3];
ktmp[4] = kernel1[r*4+0];
ktmp[5] = kernel1[r*4+1];
ktmp[6] = kernel1[r*4+2];
ktmp[7] = kernel1[r*4+3];
ktmp[8] = kernel2[r*4+0];
ktmp[9] = kernel2[r*4+1];
ktmp[10] = kernel2[r*4+2];
ktmp[11] = kernel2[r*4+3];
ktmp[12] = kernel3[r*4+0];
ktmp[13] = kernel3[r*4+1];
ktmp[14] = kernel3[r*4+2];
ktmp[15] = kernel3[r*4+3];
ktmp[16] = kernel4[r*4+0];
ktmp[17] = kernel4[r*4+1];
ktmp[18] = kernel4[r*4+2];
ktmp[19] = kernel4[r*4+3];
ktmp[20] = kernel5[r*4+0];
ktmp[21] = kernel5[r*4+1];
ktmp[22] = kernel5[r*4+2];
ktmp[23] = kernel5[r*4+3];
ktmp[24] = kernel6[r*4+0];
ktmp[25] = kernel6[r*4+1];
ktmp[26] = kernel6[r*4+2];
ktmp[27] = kernel6[r*4+3];
ktmp[28] = kernel7[r*4+0];
ktmp[29] = kernel7[r*4+1];
ktmp[30] = kernel7[r*4+2];
ktmp[31] = kernel7[r*4+3];
ktmp += 32;
kernel0 += 36;
kernel1 += 36;
kernel2 += 36;
kernel3 += 36;
kernel4 += 36;
kernel5 += 36;
kernel6 += 36;
kernel7 += 36;
}
}
for (; p+3<outch; p+=4)
{
const float* kernel0 = (const float*)kernel_tm.channel(p);
const float* kernel1 = (const float*)kernel_tm.channel(p+1);
const float* kernel2 = (const float*)kernel_tm.channel(p+2);
const float* kernel3 = (const float*)kernel_tm.channel(p+3);
float* ktmp = kernel_tm_test.channel(p/8 + (p%8)/4);
for (int q=0; q<inch; q++)
{
ktmp[0] = kernel0[r*4+0];
ktmp[1] = kernel0[r*4+1];
ktmp[2] = kernel0[r*4+2];
ktmp[3] = kernel0[r*4+3];
ktmp[4] = kernel1[r*4+0];
ktmp[5] = kernel1[r*4+1];
ktmp[6] = kernel1[r*4+2];
ktmp[7] = kernel1[r*4+3];
ktmp[8] = kernel2[r*4+0];
ktmp[9] = kernel2[r*4+1];
ktmp[10] = kernel2[r*4+2];
ktmp[11] = kernel2[r*4+3];
ktmp[12] = kernel3[r*4+0];
ktmp[13] = kernel3[r*4+1];
ktmp[14] = kernel3[r*4+2];
ktmp[15] = kernel3[r*4+3];
ktmp += 16;
kernel0 += 36;
kernel1 += 36;
kernel2 += 36;
kernel3 += 36;
}
}
for (; p<outch; p++)
{
const float* kernel0 = (const float*)kernel_tm.channel(p);
float* ktmp = kernel_tm_test.channel(p/8 + (p%8)/4 + p%4);
for (int q=0; q<inch; q++)
{
ktmp[0] = kernel0[r*4+0];
ktmp[1] = kernel0[r*4+1];
ktmp[2] = kernel0[r*4+2];
ktmp[3] = kernel0[r*4+3];
ktmp += 4;
kernel0 += 36;
}
}
kernel_tm2.push_back(kernel_tm_test);
}
}
static void conv3x3s1_winograd43_sse(const Mat& bottom_blob, Mat& top_blob, const std::vector<Mat> &kernel_tm_test, const Mat& _bias, const Option& opt)
{
int w = bottom_blob.w;
int h = bottom_blob.h;
int inch = bottom_blob.c;
int outw = top_blob.w;
int outh = top_blob.h;
int outch = top_blob.c;
size_t elemsize = bottom_blob.elemsize;
const float* bias = _bias;
// pad to 4n+2, winograd F(4,3)
Mat bottom_blob_bordered = bottom_blob;
outw = (outw + 3) / 4 * 4; //变成4的倍数
outh = (outh + 3) / 4 * 4;
w = outw + 2;
h = outh + 2;
Option opt_b = opt;
opt_b.blob_allocator = opt.workspace_allocator;
copy_make_border(bottom_blob, bottom_blob_bordered, 0, h - bottom_blob.h, 0, w - bottom_blob.w, 0, 0.f, opt_b);
// BEGIN transform input
Mat bottom_blob_tm;
{
int w_tm = outw / 4 * 6;
int h_tm = outh / 4 * 6;
//输入经过了转置,所以输出也转置,对应到原图,h,w是要交换的
int nColBlocks = h_tm/6; // may be the block num in Feathercnn
int nRowBlocks = w_tm/6;
const int tiles = nColBlocks * nRowBlocks;
bottom_blob_tm.create(4, inch, tiles*9, elemsize, opt.workspace_allocator); //存输入transform的结果
// BT
// const float itm[4][4] = {
// {4.0f, 0.0f, -5.0f, 0.0f, 1.0f, 0.0f},
// {0.0f,-4.0f, -4.0f, 1.0f, 1.0f, 0.0f},
// {0.0f, 4.0f, -4.0f,-1.0f, 1.0f, 0.0f},
// {0.0f,-2.0f, -1.0f, 2.0f, 1.0f, 0.0f},
// {0.0f, 2.0f, -1.0f,-2.0f, 1.0f, 0.0f},
// {0.0f, 4.0f, 0.0f,-5.0f, 0.0f, 1.0f}
// };
// 0 = 4 * r00 - 5 * r02 + r04
// 1 = -4 * (r01 + r02) + r03 + r04
// 2 = 4 * (r01 - r02) - r03 + r04
// 3 = -2 * r01 - r02 + 2 * r03 + r04
// 4 = 2 * r01 - r02 - 2 * r03 + r04
// 5 = 4 * r01 - 5 * r03 + r05
// 0 = 4 * r00 - 5 * r02 + r04
// 1 = -4 * (r01 + r02) + r03 + r04
// 2 = 4 * (r01 - r02) - r03 + r04
// 3 = -2 * r01 - r02 + 2 * r03 + r04
// 4 = 2 * r01 - r02 - 2 * r03 + r04
// 5 = 4 * r01 - 5 * r03 + r05
#pragma omp parallel for num_threads(opt.num_threads)
for (int q=0; q<inch; q++)
{
const float* img = bottom_blob_bordered.channel(q);
for (int j = 0; j < nColBlocks; j++)
{
const float* r0 = img + w * j * 4; //step是4 ,重叠度为2
const float* r1 = r0 + w;
const float* r2 = r1 + w;
const float* r3 = r2 + w;
const float* r4 = r3 + w;
const float* r5 = r4 + w;
for (int i = 0; i < nRowBlocks; i++)
{
float* out_tm0 = bottom_blob_tm.channel(tiles*0+j*nRowBlocks+i).row(q); //4个输出
float* out_tm1 = bottom_blob_tm.channel(tiles*1+j*nRowBlocks+i).row(q);
float* out_tm2 = bottom_blob_tm.channel(tiles*2+j*nRowBlocks+i).row(q);
float* out_tm3 = bottom_blob_tm.channel(tiles*3+j*nRowBlocks+i).row(q);
float* out_tm4 = bottom_blob_tm.channel(tiles*4+j*nRowBlocks+i).row(q);
float* out_tm5 = bottom_blob_tm.channel(tiles*5+j*nRowBlocks+i).row(q);
float* out_tm6 = bottom_blob_tm.channel(tiles*6+j*nRowBlocks+i).row(q);
float* out_tm7 = bottom_blob_tm.channel(tiles*7+j*nRowBlocks+i).row(q);
float* out_tm8 = bottom_blob_tm.channel(tiles*8+j*nRowBlocks+i).row(q);
float d0[6],d1[6],d2[6],d3[6],d4[6],d5[6];
float w0[6],w1[6],w2[6],w3[6],w4[6],w5[6];
float t0[6],t1[6],t2[6],t3[6],t4[6],t5[6];
// load
for (int n = 0; n < 6; n++)
{
d0[n] = r0[n];
d1[n] = r1[n];
d2[n] = r2[n];
d3[n] = r3[n];
d4[n] = r4[n];
d5[n] = r5[n];
}
// w = B_t * d
for (int n = 0; n < 6; n++)
{
w0[n] = 4*d0[n] - 5*d2[n] + d4[n];
w1[n] = -4*d1[n] - 4*d2[n] + d3[n] + d4[n];
w2[n] = 4*d1[n] - 4*d2[n] - d3[n] + d4[n];
w3[n] = -2*d1[n] - d2[n] + 2*d3[n] + d4[n];
w4[n] = 2*d1[n] - d2[n] - 2*d3[n] + d4[n];
w5[n] = 4*d1[n] - 5*d3[n] + d5[n];
}
// transpose d to d_t
{
t0[0]=w0[0]; t1[0]=w0[1]; t2[0]=w0[2]; t3[0]=w0[3]; t4[0]=w0[4]; t5[0]=w0[5];
t0[1]=w1[0]; t1[1]=w1[1]; t2[1]=w1[2]; t3[1]=w1[3]; t4[1]=w1[4]; t5[1]=w1[5];
t0[2]=w2[0]; t1[2]=w2[1]; t2[2]=w2[2]; t3[2]=w2[3]; t4[2]=w2[4]; t5[2]=w2[5];
t0[3]=w3[0]; t1[3]=w3[1]; t2[3]=w3[2]; t3[3]=w3[3]; t4[3]=w3[4]; t5[3]=w3[5];
t0[4]=w4[0]; t1[4]=w4[1]; t2[4]=w4[2]; t3[4]=w4[3]; t4[4]=w4[4]; t5[4]=w4[5];
t0[5]=w5[0]; t1[5]=w5[1]; t2[5]=w5[2]; t3[5]=w5[3]; t4[5]=w5[4]; t5[5]=w5[5];
}
// d = B_t * d_t
for (int n = 0; n < 6; n++)
{
d0[n] = 4*t0[n] - 5*t2[n] + t4[n];
d1[n] = - 4*t1[n] - 4*t2[n] + t3[n] + t4[n];
d2[n] = 4*t1[n] - 4*t2[n] - t3[n] + t4[n];
d3[n] = - 2*t1[n] - t2[n] + 2*t3[n] + t4[n];
d4[n] = 2*t1[n] - t2[n] - 2*t3[n] + t4[n];
d5[n] = 4*t1[n] - 5*t3[n] + t5[n];
}
// save to out_tm 注意,这边输出是转置的
{
out_tm0[0]=d0[0];out_tm0[1]=d0[1];out_tm0[2]=d0[2];out_tm0[3]=d0[3];
out_tm1[0]=d0[4];out_tm1[1]=d0[5];out_tm1[2]=d1[0];out_tm1[3]=d1[1];
out_tm2[0]=d1[2];out_tm2[1]=d1[3];out_tm2[2]=d1[4];out_tm2[3]=d1[5];
out_tm3[0]=d2[0];out_tm3[1]=d2[1];out_tm3[2]=d2[2];out_tm3[3]=d2[3];
out_tm4[0]=d2[4];out_tm4[1]=d2[5];out_tm4[2]=d3[0];out_tm4[3]=d3[1];
out_tm5[0]=d3[2];out_tm5[1]=d3[3];out_tm5[2]=d3[4];out_tm5[3]=d3[5];
out_tm6[0]=d4[0];out_tm6[1]=d4[1];out_tm6[2]=d4[2];out_tm6[3]=d4[3];
out_tm7[0]=d4[4];out_tm7[1]=d4[5];out_tm7[2]=d5[0];out_tm7[3]=d5[1];
out_tm8[0]=d5[2];out_tm8[1]=d5[3];out_tm8[2]=d5[4];out_tm8[3]=d5[5];
}
r0 += 4;
r1 += 4;
r2 += 4;
r3 += 4;
r4 += 4;
r5 += 4;
}
}
}
}
bottom_blob_bordered = Mat();
// BEGIN dot
Mat top_blob_tm;
{
int w_tm = outw / 4 * 6;
int h_tm = outh / 4 * 6;
int nColBlocks = h_tm/6; // may be the block num in Feathercnn
int nRowBlocks = w_tm/6;
const int tiles = nColBlocks * nRowBlocks;
top_blob_tm.create(36, tiles, outch, elemsize, opt.workspace_allocator);
#pragma omp parallel for num_threads(opt.num_threads)
for (int r=0; r<9; r++)
{
int nn_outch = 0;
int remain_outch_start = 0;
nn_outch = outch >> 3;
remain_outch_start = nn_outch << 3; // /8 * 8
for (int pp=0; pp<nn_outch; pp++)
{
int p = pp * 8;
float* output0_tm = top_blob_tm.channel(p);
float* output1_tm = top_blob_tm.channel(p+1);
float* output2_tm = top_blob_tm.channel(p+2);
float* output3_tm = top_blob_tm.channel(p+3);
float* output4_tm = top_blob_tm.channel(p+4);
float* output5_tm = top_blob_tm.channel(p+5);
float* output6_tm = top_blob_tm.channel(p+6);
float* output7_tm = top_blob_tm.channel(p+7);
output0_tm = output0_tm + r*4; //8个通道一起输出
output1_tm = output1_tm + r*4;
output2_tm = output2_tm + r*4;
output3_tm = output3_tm + r*4;
output4_tm = output4_tm + r*4;
output5_tm = output5_tm + r*4;
output6_tm = output6_tm + r*4;
output7_tm = output7_tm + r*4;
for (int i=0; i<tiles; i++)
{
const float* kptr = kernel_tm_test[r].channel(p/8);
const float* r0 = bottom_blob_tm.channel(tiles*r+i); //好奇,为什么要4个4个乘
float sum0[4] = {0};
float sum1[4] = {0};
float sum2[4] = {0};
float sum3[4] = {0};
float sum4[4] = {0};
float sum5[4] = {0};
float sum6[4] = {0};
float sum7[4] = {0};
for (int q=0; q<inch; q++)
{
for (int n=0; n<4; n++)
{
sum0[n] += r0[n] * kptr[n]; //32个数放一起,8个核 * 4
sum1[n] += r0[n] * kptr[n+4];
sum2[n] += r0[n] * kptr[n+8];
sum3[n] += r0[n] * kptr[n+12];
sum4[n] += r0[n] * kptr[n+16];
sum5[n] += r0[n] * kptr[n+20];
sum6[n] += r0[n] * kptr[n+24];
sum7[n] += r0[n] * kptr[n+28];
}
kptr += 32;
r0 += 4;
}
for (int n=0; n<4; n++)
{
output0_tm[n] = sum0[n];
output1_tm[n] = sum1[n];
output2_tm[n] = sum2[n];
output3_tm[n] = sum3[n];
output4_tm[n] = sum4[n];
output5_tm[n] = sum5[n];
output6_tm[n] = sum6[n];
output7_tm[n] = sum7[n];
}
output0_tm += 36;
output1_tm += 36;
output2_tm += 36;
output3_tm += 36;
output4_tm += 36;
output5_tm += 36;
output6_tm += 36;
output7_tm += 36;
}
}
nn_outch = (outch - remain_outch_start) >> 2; //剩下的 /4
for (int pp=0; pp<nn_outch; pp++)
{
int p = remain_outch_start + pp * 4;
float* output0_tm = top_blob_tm.channel(p);
float* output1_tm = top_blob_tm.channel(p+1);
float* output2_tm = top_blob_tm.channel(p+2);
float* output3_tm = top_blob_tm.channel(p+3);
output0_tm = output0_tm + r*4;
output1_tm = output1_tm + r*4;
output2_tm = output2_tm + r*4;
output3_tm = output3_tm + r*4;
for (int i=0; i<tiles; i++)
{
const float* kptr = kernel_tm_test[r].channel(p/8 + (p%8)/4);
const float* r0 = bottom_blob_tm.channel(tiles*r+i);
float sum0[4] = {0};
float sum1[4] = {0};
float sum2[4] = {0};
float sum3[4] = {0};
for (int q=0; q<inch; q++)
{
for (int n=0; n<4; n++)
{
sum0[n] += r0[n] * kptr[n];
sum1[n] += r0[n] * kptr[n+4];
sum2[n] += r0[n] * kptr[n+8];
sum3[n] += r0[n] * kptr[n+12];
}
kptr += 16;
r0 += 4;
}
for (int n=0; n<4; n++)
{
output0_tm[n] = sum0[n];
output1_tm[n] = sum1[n];
output2_tm[n] = sum2[n];
output3_tm[n] = sum3[n];
}
output0_tm += 36;
output1_tm += 36;
output2_tm += 36;
output3_tm += 36;
}
}
remain_outch_start += nn_outch << 2;
for (int p=remain_outch_start; p<outch; p++) //剩下 小于 4
{
float* output0_tm = top_blob_tm.channel(p);
output0_tm = output0_tm + r*4;
for (int i=0; i<tiles; i++)
{
const float* kptr = kernel_tm_test[r].channel(p/8 + (p%8)/4 + p%4);
const float* r0 = bottom_blob_tm.channel(tiles*r+i);
float sum0[4] = {0};
for (int q=0; q<inch; q++)
{
for (int n=0; n<4; n++)
{
sum0[n] += (int)r0[n] * kptr[n];
}
kptr += 4;
r0 += 4;
}
for (int n=0; n<4; n++)
{
output0_tm[n] = sum0[n];
}
output0_tm += 36;
}
}
}
}
bottom_blob_tm = Mat();
// END dot
// BEGIN transform output
Mat top_blob_bordered;
top_blob_bordered.create(outw, outh, outch, elemsize, opt.workspace_allocator);
{
// AT
// const float itm[4][6] = {
// {1.0f, 1.0f, 1.0f, 1.0f, 1.0f, 0.0f},
// {0.0f, 1.0f, -1.0f, 2.0f, -2.0f, 0.0f},
// {0.0f, 1.0f, 1.0f, 4.0f, 4.0f, 0.0f},
// {0.0f, 1.0f, -1.0f, 8.0f, -8.0f, 1.0f}
// };
// 0 = r00 + r01 + r02 + r03 + r04
// 1 = r01 - r02 + 2 * (r03 - r04)
// 2 = r01 + r02 + 4 * (r03 + r04)
// 3 = r01 - r02 + 8 * (r03 - r04) + r05
int w_tm = outw / 4 * 6;
int h_tm = outh / 4 * 6;
int nColBlocks = h_tm/6; // may be the block num in Feathercnn
int nRowBlocks = w_tm/6;
#pragma omp parallel for num_threads(opt.num_threads)
for (int p=0; p<outch; p++)
{
float* out_tile = top_blob_tm.channel(p);
float* outRow0 = top_blob_bordered.channel(p); //输出 4 x4
float* outRow1 = outRow0 + outw;
float* outRow2 = outRow0 + outw * 2;
float* outRow3 = outRow0 + outw * 3;
const float bias0 = bias ? bias[p] : 0.f;
for (int j=0; j<nColBlocks; j++)
{
for(int i=0; i<nRowBlocks; i++)
{
// TODO AVX2
float s0[6],s1[6],s2[6],s3[6],s4[6],s5[6];
float w0[6],w1[6],w2[6],w3[6];
float d0[4],d1[4],d2[4],d3[4],d4[4],d5[4];
float o0[4],o1[4],o2[4],o3[4];
// load
for (int n = 0; n < 6; n++) //6x6 U*V
{
s0[n] = out_tile[n];
s1[n] = out_tile[n+ 6];
s2[n] = out_tile[n+12];
s3[n] = out_tile[n+18];
s4[n] = out_tile[n+24];
s5[n] = out_tile[n+30];
}
// w = A_T * W
for (int n = 0; n < 6; n++)
{
w0[n] = s0[n] + s1[n] + s2[n] + s3[n] + s4[n];
w1[n] = s1[n] - s2[n] + 2*s3[n] - 2*s4[n];
w2[n] = s1[n] + s2[n] + 4*s3[n] + 4*s4[n];
w3[n] = s1[n] - s2[n] + 8*s3[n] - 8*s4[n] + s5[n];
}
// transpose w to w_t
{
d0[0] = w0[0]; d0[1] = w1[0]; d0[2] = w2[0]; d0[3] = w3[0];
d1[0] = w0[1]; d1[1] = w1[1]; d1[2] = w2[1]; d1[3] = w3[1];
d2[0] = w0[2]; d2[1] = w1[2]; d2[2] = w2[2]; d2[3] = w3[2];
d3[0] = w0[3]; d3[1] = w1[3]; d3[2] = w2[3]; d3[3] = w3[3];
d4[0] = w0[4]; d4[1] = w1[4]; d4[2] = w2[4]; d4[3] = w3[4];
d5[0] = w0[5]; d5[1] = w1[5]; d5[2] = w2[5]; d5[3] = w3[5];
}
// Y = A_T * w_t
for (int n = 0; n < 4; n++)
{
o0[n] = d0[n] + d1[n] + d2[n] + d3[n] + d4[n];
o1[n] = d1[n] - d2[n] + 2*d3[n] - 2*d4[n];
o2[n] = d1[n] + d2[n] + 4*d3[n] + 4*d4[n];
o3[n] = d1[n] - d2[n] + 8*d3[n] - 8*d4[n] + d5[n];
}
// save to top blob tm
for (int n = 0; n < 4; n++)
{
outRow0[n] = o0[n] + bias0;
outRow1[n] = o1[n] + bias0;
outRow2[n] = o2[n] + bias0;
outRow3[n] = o3[n] + bias0;
}
out_tile += 36;
outRow0 += 4;
outRow1 += 4;
outRow2 += 4;
outRow3 += 4;
}
outRow0 += outw * 3;
outRow1 += outw * 3;
outRow2 += outw * 3;
outRow3 += outw * 3;
}
}
}
// END transform output
// cut result pad
copy_cut_border(top_blob_bordered, top_blob, 0, top_blob_bordered.h - top_blob.h, 0, top_blob_bordered.w - top_blob.w, opt);
}