Baidu Apollo轨迹规划课时5 :optimization inside motion planning
视频地址,部分参考CSDN博客
优化问题重要有三点
Objective functionconstraintdynamic planning

动态规划来自于动态系统,通过类似于有限元的方式,把问题抽象在离散空间里面,把重复计算通过aggregating的方式进行简化。
(问题:计算时长太长,复杂度高,撒点太复杂)
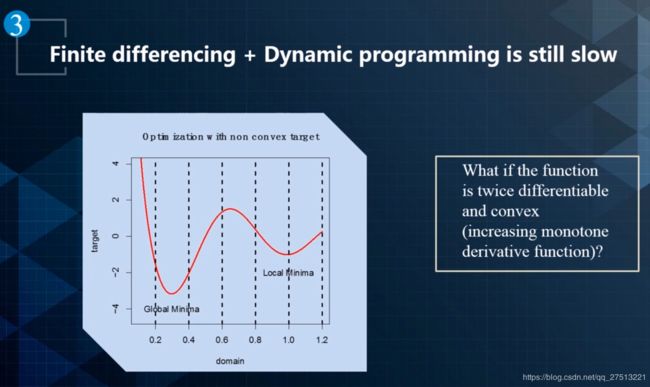
对于凸问题,或者单调问题,求最优解,用binary search搜索某个点的值就可以,收敛速度是指数收敛
牛顿法更快,考虑了不同点位置的斜率变化率大小,收敛速度是指数平方,二次收敛,比binary search快。本质上是二阶逼近的泰勒展开。
牛顿法的思想:把函数用泰勒展开然后逼近,获得更多的信息,用更快的速度去收敛最优解。
二次规划的核心:如果知道convex problems的二阶导数,可以更快地找到最优解,本质和Taylor expansion和牛顿法相同。
二次规划有时候会处理高纬度问题,问题是在多维的空间里,进行优化convex optimization的时候,很难找到一个高阶的类似hessian矩阵的东西。一维时候偏导是参数的个数,二维是参数个数的平方,三维是个tensor,非常庞大。这是个权衡的过程,实践中二维就够用了。
Quadratic Programmming的劣势
牛顿法要求derivative严格单调递增,一般的函数不是这样子的。
动态规划要求打点很多,对于高维是灾难,牛顿法只能找到局部最优,也不行。
解决方法:divide and conquer
动态规划 + 牛顿法 二次规划 可以找到global的最优解
如上图找到第一个或第二个点,这个点作为牛顿法的起始点,从这个点做一个hot start,然后做一个QP problem。这个时候有大概率找到global optimization。EM Planner里面的组合优化,启发式的搜索,DP撒点不要太密也不要太稀疏,对整个空间有个粗浅的认识后,找到hot start作为启发信息,然后QP找到最优解。启发式搜索只要reward function支部特别复杂都可以找到最优解,其它类似方法有模拟退火等。

二次规划
- QP问题,没有
constraint时,直接求导就行; - QP问题,有
constraint
二次规划找局部值或者边界值,hit boundary 的constraint 叫active constraint。在求解带约束的条件的时候,看一下满足active constraint的情况下的最优解,不满足情况下的最优解的样子,看不满足active constraint情况下的最优解在不在约束内,在的话就是最优解,不在的话看满足active constraint情况下的最优解。这种思想就active set method。
拓展到高维后的形式:

Q x + C = 0 Qx + C = 0 Qx+C=0 的求解:
牛顿消元法:QR,LR算法。拆解为一个上三角矩阵或正交矩阵,这样容易计算。
同时这个矩阵也是个symmetric strictly positive definite(对称严格正定)。对阵矩阵有更好的decomposition的方式:比如cholesky decomposition,schur decomposition。可以很快地求解线性系统。
可以通过线性代数,矩阵运算的方式进行。速度很快。把问题扩展到高维情况,最优解即高阶导数为0即可。
QP问题,有等式约束
把下面的等式带入上面的function还元,不过很慢。
举例,对于
M i n i m i z e 1 2 x T Q x + c T x Minimize \ \ \frac{1}{2} x^TQx + c ^ Tx Minimize 21xTQx+cTx
求最优解,约束是 E x = d Ex = d Ex=d
原始的方法是将元素直接带入进行换元,转换成一个全新的QP问题进行求解。但是这种方法很慢。有更快的方法,lagrangian方法,dual parameters类似松弛变量,这种情况下等式就是一个超平面。
如:
1 2 x T Q x + c T x + λ T ( E x − d ) f ( x ) − > f ( x , λ ) \frac{1}{2}x^TQx + c^Tx + \lambda ^ T(Ex - d) \\ f(x) ->f(x,\lambda) 21xTQx+cTx+λT(Ex−d)f(x)−>f(x,λ)
对其进行求导得:
Q x + λ T E = − C E x = d Qx + \lambda ^ T E = -C \\ Ex = d Qx+λTE=−CEx=d
之后再转换成线性方程组的形式进行运算:
[ Q E T E 0 ] [ x λ ] = [ − c d ] \begin{bmatrix} Q & E^T \\ E & 0 \\ \end{bmatrix} \begin{bmatrix} x \\ \lambda \end{bmatrix} = \begin{bmatrix} -c \\ d \end{bmatrix} [QEET0][xλ]=[−cd]
这个和之前的类似,当前也可能有没有解的情况。每加一个等式的约束,可行空间就降一个维度。
QP的不等式约束
使用方法:active set method
一种新的思路 :KKT condition

重点是12.30e,不等式为0,active的时候 λ \lambda λ 为任意值,不等式不为0时, λ \lambda λ 为0.
除了active set method以外还有其他办法,在松弛变量上做文章,interior point method(内点法)
最常用的思路

先当成没有inequality的去算,之后看那些inequality没有满足,这个时候这个条件被加入到active set里面。即这个条件等于0,重复直到找到最优解。
目标函数不是二次型的凸函数怎么办?
比如 ( x − 2 ) 4 (x -2)^4 (x−2)4 ,局部用牛顿法逼近,用surrograte的objective function去代替原来的function。sequential解决问题,在高维空间求解hessian。有很多方法:BFGS,LBFPS
推荐书籍:
- Convex optimization
- Stephen J. Wright Numerical Optimization

