Read + Verify: Machine Reading Comprehension with Unanswerable Questions翻译

摘要

对于无法回答问题的机器阅读理解旨在当无法推断出答案时放弃回答。除了提取答案外，以前的工作通常去预测一个额外的“无答案”概率，从而去检测无法回答情况。但是，他们无法通过验证预测答案的合法性来验证问题的可回答性。为了解决这个问题，我们提出了一种新颖的“读后验证”系统，该系统不仅利用神经阅读器提取候选答案并产生无答案的概率，而且利用答案验证器来确定输入的片段是否是预测的答案。此外，我们引入了两个附加损失函数，以帮助阅读器更好地处理答案提取和无答案检测，并研究了答案验证器的三种不同体系结构。我们在SQuAD 2.0数据集上进行的实验表明，我们的系统在测试集上获得74.2的F1分数，在提交时（2018年8月28日）达到了最先进的结果。

1.介绍

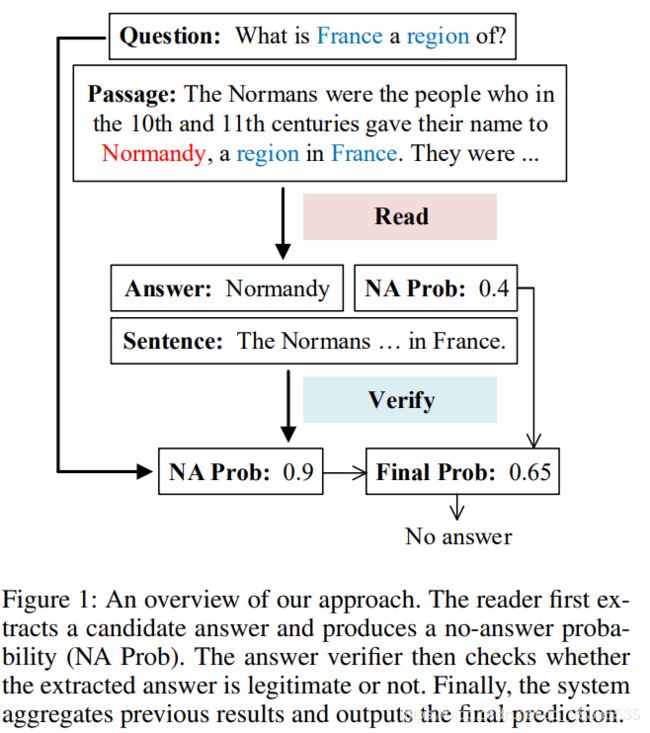
　　理解文本和回答问题的能力对于自然语言处理至关重要。由于各种大型数据集的创建，这导致在机器阅读理解的任务上取得了显著进步。但是，当前方法背后的一个重要假设是，上下文段落中始终存在正确的答案。因此，模型仅需要根据问题选择一个最合理的文本范围，而不是首先检查是否存在答案。最近，已经提出了新版本的斯坦福问答数据库（SQuAD），被称为SQuAD 2.0，以测试回答有答案问题和无答案问题的能力。为了处理无答案问题的情况，系统必须学会识别各种语言现象，例如否定，反义词以及段落和问题之间的实体变化。
　　先前的工作都在``无答案’'得分和答案跨度得分之间应用了共享归一化运算，从而产生了一个无法回答问题的概率并输出候选答案。但是，他们尚未考虑通过验证预测答案的合法性来进一步验证问题的可回答性。在这里，可回答性表示问题是否具有答案，合法性意味着所提取的文本是否可以被段落和问题支持。相反，人类倾向于首先找到一个给定问题的合理答案，然后检查是否存在任何矛盾的语义。
　　为了解决上述问题，我们提出了一种读后验证系统，旨在对本文中无法回答的问题保持鲁棒性。如图1所示，我们的系统由两个组件组成：（1）无答案阅读器，用于提取候选答案并检测无法回答的问题；（2）答案验证器，用于确定所提取的候选答案是否合法。我们工作的主要贡献是三方面的。
　　首先，我们使用两个附加损失函数来增强现有阅读器的理解能力，以更好地分别处理答案提取和无答案检测。由于下游验证阶段始终需要候选答案，因此阅读器必须能够为所有问题提取合理的答案。但是，先前的方法没有被训练用于去发现无答案问题的潜在候选项。我们通过引入独立的跨度损失来解决此问题，该损失旨在不考虑问题的可回答性而专注于答案提取任务。为了与无答案检测不冲突，我们利用多头指针网络生成两对跨度得分，其中一对用于和无答案得分标准化，另一对用于我们的附加损失。此外，我们通过关注无答案检测任务而不考虑答案提取的共享归一化，提出了另一个独立的无答案损失，以进一步缓解冲突。
　　其次，除了标准阅读阶段之外，我们还引入了另一个答案验证阶段，该阶段旨在通过将答案句子与问题进行比较来找到支持答案的局部蕴涵。这是基于这样的观察：无法回答的问题的核心现象通常发生在几个段落词和疑问词之间。以图1为例，将段落“Normandy, a region in France”与该问题进行比较后，我们可以轻松地确定不存在任何答案，因为该问题要求一个不可能的条件。当出现反义词或相互排斥时，这种观察甚至更加明显，例如问“the decline of rainforests”的问题，但短文提到“the rainforests spread out”。受自然语言推理（NLI）的最新进展启发，我们研究了三种不同的架构来进行答案验证任务。第一个是序列模型，将两个句子作为一个长序列，而第二个则试图捕获两个句子之间的交互。最后一个是混合模型，它结合了以上两个模型来测试性能是否可以进一步提高。
　　最后，我们在SQuAD 2.0数据集上评估了我们的系统，这是一个阅读理解benchmark，补充了无答案的问题。我们最好的阅读器在有以及没有ELMo嵌入的情况下在开发集上获得的F1分数分别为73.7和69.1。当与答案验证器结合使用时，整个系统的F1分别提高到74.8和71.5。此外，最佳系统在测试集上获得74.2 F1的分数，在提交时（2018年8月28日）达到了最好的结果。

2.背景

现有的阅读理解模型专注于回答保证存在正确答案的问题。但是，他们无法识别无法回答的问题，这往往会返回不可靠的文本范围。因此，我们首先简要介绍无答案的阅读理解任务，然后研究当前的解决方案。

2.1 任务描述

给定一个上下文段落和问题，机器不仅需要找到可回答问题的答案，还必须检测出无法回答的情况。段落和问题被描述为单词字符的序列，分别表示为$P=\{x_i^p{\}}_{i=1}^{l_p}$和$Q=\{x_j^q{\}}_{j=1}^{l_q}$，其中$l_p$是段落长度，$l_q$是问题长度。 我们的目标是预测答案$A$，该答案被约束为段落中的一段文本：$A=\{x_i^p{\}}_{i=l_a}^{l_b}$，或者如果没有答案则返回空字符串，其中$l_a$和$l_b$表示答案边界。

2.2 无答案阅读器

为了预测答案范围，当前方法首先将段落和问题嵌入并编码为两个固定大小的向量序列。然后，他们利用各种注意力机制，例如双向注意力或再注意力，为段落和问题建立相互依赖的表示形式，分别表示为$U=\{u_i{\}}_{i=1}^{l_p}$和$V=\{v_j{\}}_{j=1}^{l_q}$。最后，他们将问题表示形式概括为一个密集的向量$t$，并利用指针网络在段落单词词上产生两个分数来表示答案边界：
$$o_j=w_v^T{v}_j,t=\sum _{j=1}^{l_q}\frac{e^{o_j}}{{\sum }_{k=1}^{l_q}{e}^{o_k}}{v}_j$$
$$\alpha ,\beta =pointer\_newwork(U,t)$$
其中$\alpha$和$\beta$是答案开始和结束范围的跨度得分。
　　为了额外检测问题是否无法回答，除答案跨度分布外，先前的方法还尝试预测特殊的无答案分数$z$。具体来说，可以使用共享的softmax函数对无答案得分和跨度得分进行归一化，从而产生联合无答案目标函数，定义为：
$${\mathcal{L}}_{joint}=-log(\frac{(1-\delta )e^z+\delta e^{{\alpha }_a{\beta }_b}}{e^z+{\sum }_{i=1}^{l_p}{\sum }_{j=1}^{l_p}{e}^{{\alpha }_i{\beta }_j}})$$
其中$a$和$b$是答案实际的开始和结束位置，如果问题可以回答，则$\delta$为1，否则为0。在测试时，一旦标准化的无答案分数超过某个阈值，就会检测到该问题无法回答。

3.方法

　　在本节中，我们描述了我们提出的先读后验系统。该系统首先利用神经阅读器提取候选答案并检测问题是否无法回答。然后，它利用答案验证器进一步检查预测答案的合法性。我们通过使用两种新颖的附加损失函数来增强阅读器的理解力，并研究了答案验证器三种不同的体系结构。

3.1 具有附加损失的阅读器

尽管以前的无答案阅读器能够共同学习答案提取和无答案检测，但是每个任务都面临两个问题。对于答案提取，以前的阅读器没有被训练用于发现无法回答问题的候选答案。但是，在我们的系统中，要求阅读器提取所有问题的合理答案，该答案被提供给下游验证阶段。至于无答案检测，由于跨度得分和无答案得分之间的共享归一化，可能会引发冲突。由于这些归一化分数的总和始终为1，因此过高的跨度概率会导致过低的无答案概率，反之亦然。因此，Clark et al. (2018)观察到这会导致对答案范围的置信度不准确，从而导致对无答案分数的预测不准确。为了解决上述问题，我们提出了两个附加损失，以独立优化和增强每个任务，而又彼此不干扰。
　　（1）独立跨度损失
　　该损失旨在集中于答案提取。在此任务中，要求模型为所有可能的问题提取候选答案。因此，除了可以回答的问题之外，我们还考虑了无法回答的情况，并将合理回答视为标准答案。为了不与无答案检测冲突，我们建议使用多头指针网络来另外产生另一对跨度得分$\tilde{\alpha }$和$\tilde{\beta }$：
$${\tilde{o}}_j={\tilde{w}}_v^T{v}_j,\tilde{t}=\sum _{j=1}^{l_q}\frac{e^{{\tilde{o}}_j}}{{\sum }_{k=1}^{l_q}{e}^{{\tilde{o}}_k}}{v}_j$$
$$\tilde{\alpha },\tilde{\beta }=pointer\_newwork(U,\tilde{t})$$
其中多头指针网络共享相同的网络架构，但参数不同。
　　然后，我们将独立的跨度损失定义为：
$${\mathcal{L}}_{indep-I}=-log(\frac{e^{{\tilde{\alpha }}_{\tilde{a}}{\tilde{\beta }}_{\tilde{b}}}}{{\sum }_{i=1}^{l_p}{\sum }_{j=1}^{l_p}{e}^{{\tilde{\alpha }}_i{\tilde{\beta }}_j}})$$
其中$\tilde{a}$和$\tilde{b}$是增强的真实答案边界。最终的跨度概率是使用两对softmax归一化跨度得分上的简单均值池化获得的。
　　（2）独立无答案损失
　　尽管使用了多头指针网络来防止冲突问题，但是由于无答案得分$z$已通过跨度得分进行了归一化，因此无答案检测仍然会受到削弱。因此，我们考虑专门鼓励对无答案检测的预测。这是通过引入独立的无答案损失来实现的：
$${\mathcal{L}}_{indep-II}=-(1-\delta )log\sigma (z)-\delta log(1-\sigma (z))$$
其中$\sigma$是sigmoid激活函数。通过此损失，我们希望模型在不考虑共享归一化操作的情况下对无答案得分$z$产生更可靠的预测。
　　最后，我们将上述损失合并如下：
$$\mathcal{L}={\mathcal{L}}_{joint}+\gamma {\mathcal{L}}_{indep-I}+\lambda {\mathcal{L}}_{indep-II}$$
其中$\gamma$和$\lambda$是控制两个附加损耗权重的两个超参数。

3.2 答案验证器

提取答案后，使用答案验证器将答案句子与问题进行比较，以识别支持答案的局部文本蕴含。在这里，我们将答案句子定义为包含标准答案或合理答案的上下文句子。我们探索了三种不同的体系结构，如图2所示：（1）一个将输入作为长序列的序列化模型，（2）一个对句子进行相互编码的交互式模型，（3）一个将上述两种方法都考虑在内的混合模型。
　　（1）Model-I：序列化体系结构
　　在Model-I中，我们将答案句子和问题以及提取的答案转换为有序的输入序列。然后，我们将最近提出的Generative Pre-trained Transformer（OpenAI GPT）修改为执行任务。该模型是多层Transformer解码器，首先使用针对大型未标记文本语料库的语言建模目标进行训练，然后针对特定目标任务进行微调。
　　具体来说，给定一个答案句子$S$，一个问题$Q$和一个提取的答案$A$，我们将两个句子与答案连接起来，同时在两者之间添加定界符标记以获得[$S$;$Q$;$;$A$]。 然后，我们将序列的单词嵌入和位置嵌入一起编码。多个Transformer块用于对序列嵌入进行编码，如下所示：
$$h_0=W_e[X]+W_p$$
$$h_i=transformer\_block(h_{i-1}),\forall i\in [1,n]$$
其中$X$表示词汇中的序列索引，$W_e$是字符嵌入矩阵，$W_p$是位置嵌入矩阵，$n$是transformer块数。每个块由一个屏蔽的多头self-attention层和一个逐个位置前馈的层组成。每一层之后使用残差连接和层规范化。
　　然后将最后一个字符的激活$h_n^{l_m}$带入线性映射层，然后输入softmax函数以输出无答案概率$y$：
$$p(y|X)=softmax(h_n^{l_m}{W}_y)$$
　　一个标准的交叉熵目标函数被用于最小化负对数概率：
$$\mathcal{L}(\theta )=-\sum _{(X,y)}logp(y|X)$$
　　（2）Model-II：交互式体系结构
　　在Model-II中，我们考虑了一个交互式体系结构，该体系结构旨在捕获两个句子之间的交互，以便识别它们的局部蕴含关系以验证答案。该模型包括以下几层：
　　编码器：我们使用GloVe嵌入嵌入单词，并使用可训练的矢量嵌入每个单词的字符。我们运行双向LSTM（BiLSTM）对字符进行编码，并连接两个最后的隐藏状态以获得单词级嵌入。此外，我们使用二元特征来表示单词是否是答案的一部分。然后，所有嵌入和特征一起由权重共享的BiLSTM连接并编码，从而产生两个上下文表示序列：
$$s_i=BiLSTM([wor{d}_i^s;cha{r}_i^s;fe{q}_i^s]),\forall i\in [1,l_s]$$
$$q_j=BiLSTM(wor{d}_j^q;cha{r}_j^q;fe{q}_j^q),\forall j\in [1,l_q]$$
其中，$l_s$是答案句子的长度，$[\cdot ;\cdot ]$表示串联连接。
　　推理建模：推理建模层用于捕获两个句子之间的交互，并产生两个推理感知的句子表示。 我们首先计算所有元组$<s_i,q_j>$的点积作为注意力权重，然后对这些权重进行归一化，以获取伴随向量，如下所示：
$$a_{ij}=s_i^{\top }{q}_j,\forall i\in [1,l_s],\forall j\in [1,l_q]$$
$$b_i=\sum _{j=1}^{l_q}\frac{e^{a_{ij}}}{{\sum }_{k=1}^{l_q}{e}^{a_{ik}}}{q}_j,c_j=\sum _{i=1}^{l_s}\frac{e^{a_{ij}}}{{\sum }_{k=1}^{l_s}{e}^{a_{kj}}}{s}_i$$
在这里，$b_i$表示答案句子$S$中第$i$个单词的来自问题$Q$的伴随向量，$c_j$反之亦然。
　　接下来，为了分别比较对齐对$\{(s_i,b_i){\}}_{i=1}^{l_s}$和$\{(q_j,c_j){\}}_{j=1}^{l_q}$以查找局部推断信息，我们使用权重共享的函数$F$对这些对齐对建模：
$${\tilde{s}}_i=F(s_i,b_i),{\tilde{q}}_j=F(q_j,c_j)$$
F可以具有各种形式，例如BiLSTM，多层感知器等。在这里，我们使用Hu et al. (2018a)提出的启发式函数$o=F(x,y)$，与其他函数相比，其表现更出色：
$$\begin{gathered} r=gelu(W_r[x;y;x◦y;x-y]) \\ g=\sigma (W_g[x;y;x◦y;x-y]) \\ o=g◦r+(1-g)◦x \end{gathered}$$
其中$gelu$是高斯误差线性单元，$◦$是逐元素乘法，并且省略了偏差项。
　　句内建模：接下来，我们应用句内建模层来捕获每个句子中的自相关。输入是推断感知向量${\tilde{s}}_i$和${\tilde{q}}_j$，它们首先通过另一个BiLSTM层进行编码。然后，我们仅在每个句子与其本身之间使用上述相同的注意机制，并且如果$i=j$，则设置$a_{ij}=-inf$以确保单词与自身不对齐。另一个函数$F$用于分别产生自我感知向量${\hat{s}}_i$和${\hat{q}}_j$。
　　预测：在最终预测之前，我们应用串联的残差连接，并使用BiLSTM将句子建模为：
$${\bar{s}}_i=BiLSTM([{\tilde{s}}_i;{\hat{s}}_i]),q_j=BiLSTM([{\tilde{q}}_j;{\hat{q}}_j])$$
　　然后应用均值-最大池化操作来整合两个句子的最终表示，即${\bar{s}}_i$和${\bar{q}}_j$。然后将所有整合的向量连接起来，并馈入一个前馈分类器，该分类器由具有$gelu$激活函数的子层映射子层和softmax输出子层组成，从而产生无答案概率。如前所述，我们优化了负对数似然目标函数。
　　（3）Model-III：混合体系结构
　　为了探索如何将Model-I和Model-II提取的特征进行整合以获得更好的表示能力，我们研究了以上两个模型的组合，即Model-III。我们将两个模型的输出向量合并为一个串联表示。然后应用统一的前馈分类器以输出无答案概率。这种设计使我们能够测试性能是否可以从两种不同体系结构的集成中受益。在实践中，我们使用简单的串联来合并两个信息源。