再谈三种基础背包问题
背包问题是经典的动态规划问题,现在来复习一下。
dd大牛的背包九讲将背包问题分为八类:01背包问题 完全背包问题 多重背包问题 混合三种背包问题 二维费用的背包问题 分组的背包问题 有依赖的背包问题 泛化物品 。本次主要复习内容为前三类的基础背包问题。
1.0-1背包
有n种物品,每种只有一个.第i种物品的体积为Vi,重量为Wi.选一些物品装到一个容量为C的背包,使得背包内物品在总体积不超过C的前提下重量尽量大 .1 <= n <= 100, 1 <= Vi <=10000,1 <= Wi <= 2e6。
分析:
确认状态:求什么就设什么,设dp[i][c]为装第i个物品时的最大重量,c为当时还剩下的体积量。
最优子结构特征:要想面对第i个物品在容量没有满的情况下得到最大的重量,那么在选取第i-1的物品的时候一定是达到最大重量的。
一个递归解:在面对第i个物品时,我们只会面临两个问题:选 还是 不选
选择:在总重量中加上w[i],并且从剩余体积量c中去除v[i]
不选:那么面对第i个的最大重量就是第i-1的最大重量
可以总结为下图:
得出状态转移方程:dp[i][c] = max(dp[i-1][c-v[i]] + w[i],dp[i-1][c])。
『朴素代码』
/*
0-1背包问题:
有n种物品,每种只有一个.第i种物品的体积为Vi,重量为Wi.选一些物品装到一个容量为C的背包,
使得背包内物品在总体积不超过C的前提下重量尽量大 .1 <= n <= 100, 1 <= Vi <=10000,1 <= Wi <= 2e6
***************************************************************
*/
#include
#include
#include
#include
#include
using namespace std;
int dp[105][10010];
int v[105],w[105];
int main() {
int n,c,t;//c为容量,n为物品数
cin>>c>>n;
t = c;
memset(dp,0,sizeof(dp));
for(int i = 1;i <= n; i++){
cin>>v[i]>>w[i];
}
for(int i = 1; i <= n; i++){
for(int j = 0; j <= c; j++){
dp[i][j] = dp[i-1][j];
if(j >= v[i])
dp[i][j] = max(dp[i-1][j-v[i]] + w[i],dp[i][j]);
}
}
for(int i = 1; i <= n; i++){
cout<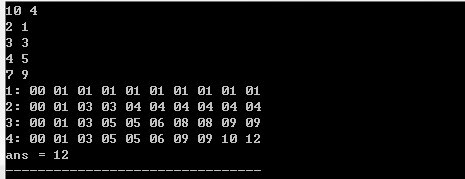
『滚动数组优化后代码』
/*
0-1背包问题:
有n种物品,每种只有一个.第i种物品的体积为Vi,重量为Wi.选一些物品装到一个容量为C的背包,
使得背包内物品在总体积不超过C的前提下重量尽量大 .1 <= n <= 100, 1 <= Vi <=10000,1 <= Wi <= 2e6
***************************************************************
*/
#include
#include
#include
#include
#include
using namespace std;
int main(){
int n,m;
cin>>m>>n;
int v[n+1],w[n+1],f[m+5];
memset(f,0,sizeof(f));
for(int i = 1;i <= n; i++){
cin>>v[i]>>w[i];
}
for(int i = 1; i <= n; i++){
for(int j = m; j >= 0; j--){
if(j >= v[i])
f[j] = max(f[j],f[j-v[i]]+w[i]);
}
cout<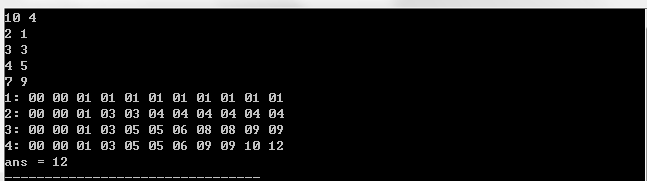
2.完全背包问题
有n种物品,每种有无限多个.第i种的物品体积为Vi,重量为Wi.选一些物品装到一个容量为c的背包中,使得背包内的
物品在总体积不超过c的情况下尽量大.1 <= n <= 100,1 <= V1 <= 10000,1 <= Wi <<10^6。
分析:
完全背包问题和0-1背包问题的差别就是在完全背包每种物品有无限多个。也就是说一种物品可以在容量充足的情况下选择无限多次。
而一个巧妙的方法就是将下面代码中的 j 的遍历次序从逆序改成顺序,这样就可以使得一个物品被使用多次。
for(int j = m; j >= 0; j--){
if(j >= v[i])
f[j] = max(f[j],f[j-v[i]]+w[i]);
}
下面举个栗子进行比较:
样例:
V= 10,N = 4
2 1
3 3
4 5
7 9
表一:i = 1 ,f[j]按逆序次序遍历更新滚动数组
1
2
3
4
5
6
7
8
9
10
0
0
0
0
0
0
0
0
0
0
1
2
3
4
5
6
7
8
9
10
0
0
0
0
0
0
0
0
0
1
1
2
3
4
5
6
7
8
9
10
0
0
0
0
0
0
0
0
1
1
1
2
3
4
5
6
7
8
9
10
0
0
0
0
0
0
0
1
1
1
1
2
3
4
5
6
7
8
9
10
0
0
0
0
0
0
1
1
1
1
1
2
3
4
5
6
7
8
9
10
0
0
0
0
0
1
1
1
1
1
1
2
3
4
5
6
7
8
9
10
0
0
0
0
1
1
1
1
1
1
1
2
3
4
5
6
7
8
9
10
0
0
0
0
1
1
1
1
1
1
1
2
3
4
5
6
7
8
9
10
0
0
0
1
1
1
1
1
1
1
1
2
3
4
5
6
7
8
9
10
0
0
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
8
9
10
0
1
1
1
1
1
1
1
1
1
j按逆序遍历,此时在计算f[j]之前,f[k](k < j)的值都还没有更新,其意义是之前没有选取过第i个物品,这样就保证了选取物品时只选取一次。
表二:i= 1,j按顺序更新数组
1
2
3
4
5
6
7
8
9
10
0
0
0
0
0
0
0
0
0
0
1
2
3
4
5
6
7
8
9
10
0
1
0
0
0
0
0
0
0
0
1
2
3
4
5
6
7
8
9
10
0
1
1
0
0
0
0
0
0
0
1
2
3
4
5
6
7
8
9
10
0
1
1
2
0
0
0
0
0
0
1
2
3
4
5
6
7
8
9
10
0
1
1
2
2
0
0
0
0
0
1
2
3
4
5
6
7
8
9
10
0
1
1
2
2
3
0
0
0
0
1
2
3
4
5
6
7
8
9
10
0
1
1
2
2
3
3
0
0
0
1
2
3
4
5
6
7
8
9
10
0
1
1
2
2
3
3
4
0
0
1
2
3
4
5
6
7
8
9
10
0
1
1
2
2
3
3
4
0
0
1
2
3
4
5
6
7
8
9
10
0
1
1
2
2
3
3
4
4
0
1
2
3
4
5
6
7
8
9
10
0
1
1
2
2
3
3
4
4
5
j按顺序更新,此时在计算f[j]之前,f[k](k < j)已经更新过了,表示之前已经选取过一次第i物品,从而实现了物品的重叠选择。
以i = 1,j = 4举例:
f[j] = max(f[j],f[j - v[i]] + w[i]) = max(f[4],f[4 - 2] + w[1]) ;
f[4] = 0,f[2] + w[1]=2,f[4] = 2;
f[2]意义就是已经选取了第1种物品1次,f[4]则代表着又选了1次第一种物品。
3.多重背包
有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用,每件费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
多重背包问题其实很轻易可以转化成k个0-1背包问题,再次举个栗子:
多重背包样例:
V = 10,N = 4
//体积 重量 数量
2 1 2
3 3 1
4 2 2
7 9 1
可以等价成:
0-1背包转化:
V = 10,N = 6
2 1
2 1
3 3
4 2
4 2
7 9
所以在之前0-1背包的代码中再加一层k循环来判断是否将第i类物品的k个取完即可
『代码』
/*
多重背包问题:
有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用,每件费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
例题:XYNUOJ 1428: 庆功会
*/
#include
#include
#include
#include
#include
using namespace std;
int main(){
int n,m;
cin>>n>>m;
int v[n+1],w[n+1],f[m+5],num[n+1];
memset(f,0,sizeof(f));
for(int i = 1;i <= n; i++){
cin>>v[i]>>w[i]>>num[i];
}
for(int i = 1; i <= n; i++){
for(int j = m; j >= 0; j--){
for(int k = 1; j - k*v[i] >= 0 && k <= num[i]; k++)
f[j] = max(f[j],f[j-k*v[i]]+k*w[i]);
}
}
cout<<"ans = "<
END.
