数据结构与算法(Python版)四十九:树的遍历
树的遍历Tree Traversals
对一个数据集中的所有数据项进行访问的操作称为“遍历Traversal”
线性数据结构中, 对其所有数据项的访问比较简单直接
按照顺序依次进行即可
树的非线性特点, 使得遍历操作较为复杂
我们按照对节点访问次序的不同来区分3种遍历
- 前序遍历(preorder):先访问根节点,再递归地前序访问左子树、最后前序访问右子树;
- 中序遍历(inorder):先递归地中序访问左子树,再访问根节点,最后中序访问右子树;
- 后序遍历(postorder):先递归地后序访问左子树,再后序访问右子树,最后访问根节点。
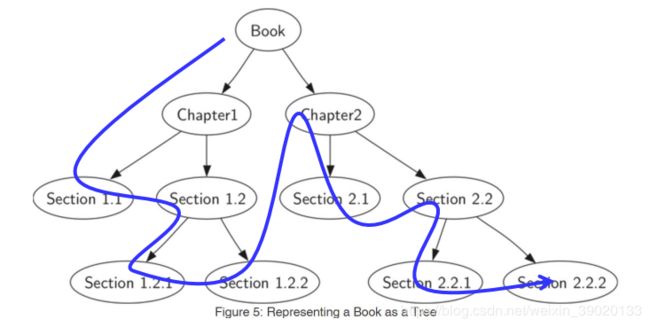
前序遍历的例子:一本书的章节阅读
Book-> Ch1-> S1.1-> S1.2-> S1.2.1-> S1.2.2-> Ch2-> S2.1-> S2.2->S2.2.1-> S2.2.2
树的遍历:递归算法代码
树遍历的代码非常简洁!
def preorder(tree):
if tree:
print(tree.getRootVal())
preorder(tree.getLeftChild())
preorder(tree.getRightChild())
后序和中序遍历的代码仅需要调整顺序
def postorder(tree):
if tree:
postorder(tree.getLeftChild())
postorder(tree.getRightChild())
print(tree.getRootVal())
def inorder(tree):
if tree:
inorder(tree.getLeftChild())
print(tree.getRootVal())
inorder(tree.getRightChild())
也可以在BinaryTree类中实现前序遍历的方法:
需要加入子树是否为空的判断
def preorder(self):
print(self.key)
if self.leftChild:
self.leftChild.preorder()
if self.rightChild:
self.rightChild.preorder()
后序遍历:表达式求值
回顾前述的表达式解析树求值, 实际上也是一个后序遍历的过程
采用后序遍历法重写表达式求值代码:
def postordereval(tree):
opers = {'+': operator.add, '-': operator.sub, '*': operator.mul, '/': operator.truediv}
if tree:
# 左子树
res1 = postordereval(tree.getLeftChild())
# 右子树
res2 = postordereval(tree.getRightChild())
if res1 and res2:
# 根节点
return opers[tree.getRootVal()](res1, res2)
else:
return tree.getRootVal()
中序遍历:生成全括号中缀表达式
采用中序遍历递归算法来生成全括号中缀表达式
下列代码中对每个数字也加了括号,请自行修改代码去除(课后练习)
def printexp(tree):
sVal = ""
if tree:
sVal = '(' + printexp(tree.getLeftChild())
sVal = sVal + str(tree.getRootVal())
sVal = sVal + printexp(tree.getRightChild()) + ')'
return sVal