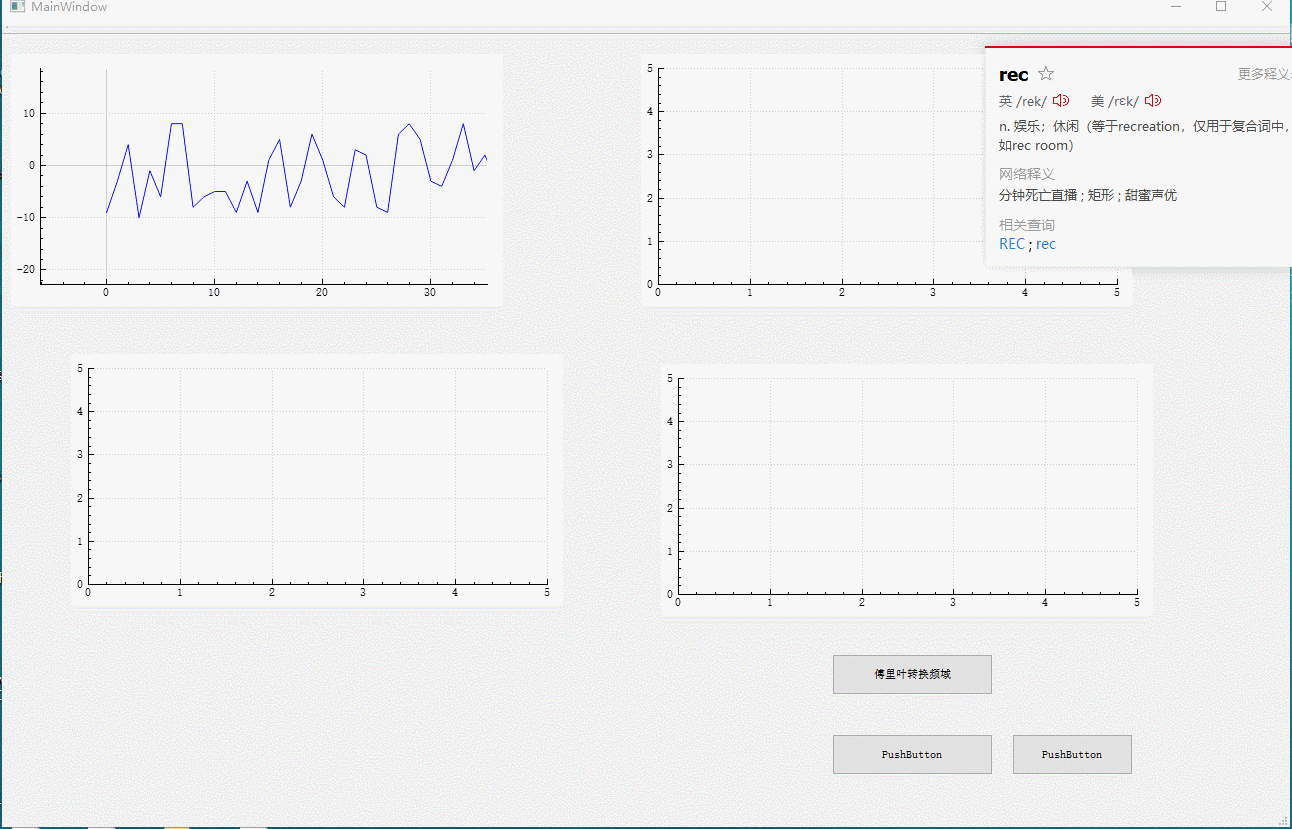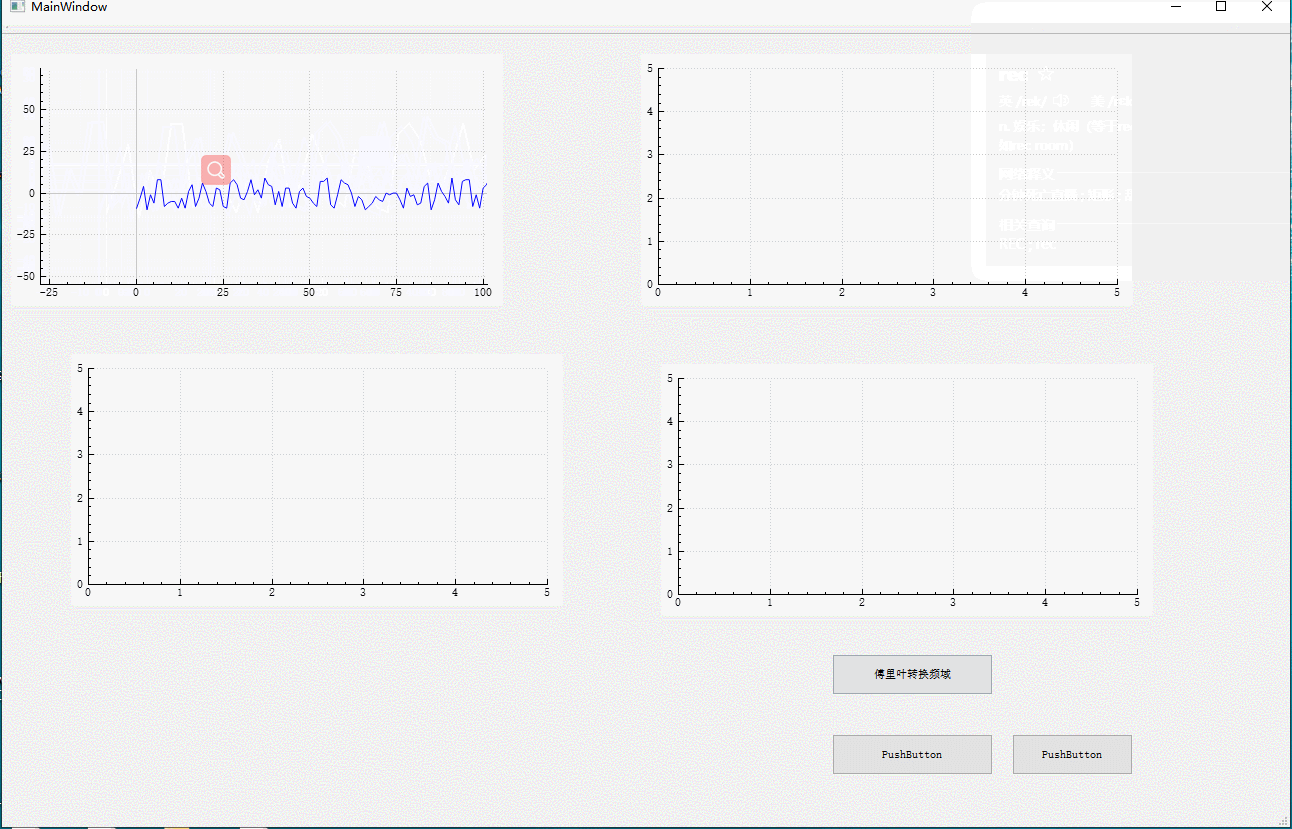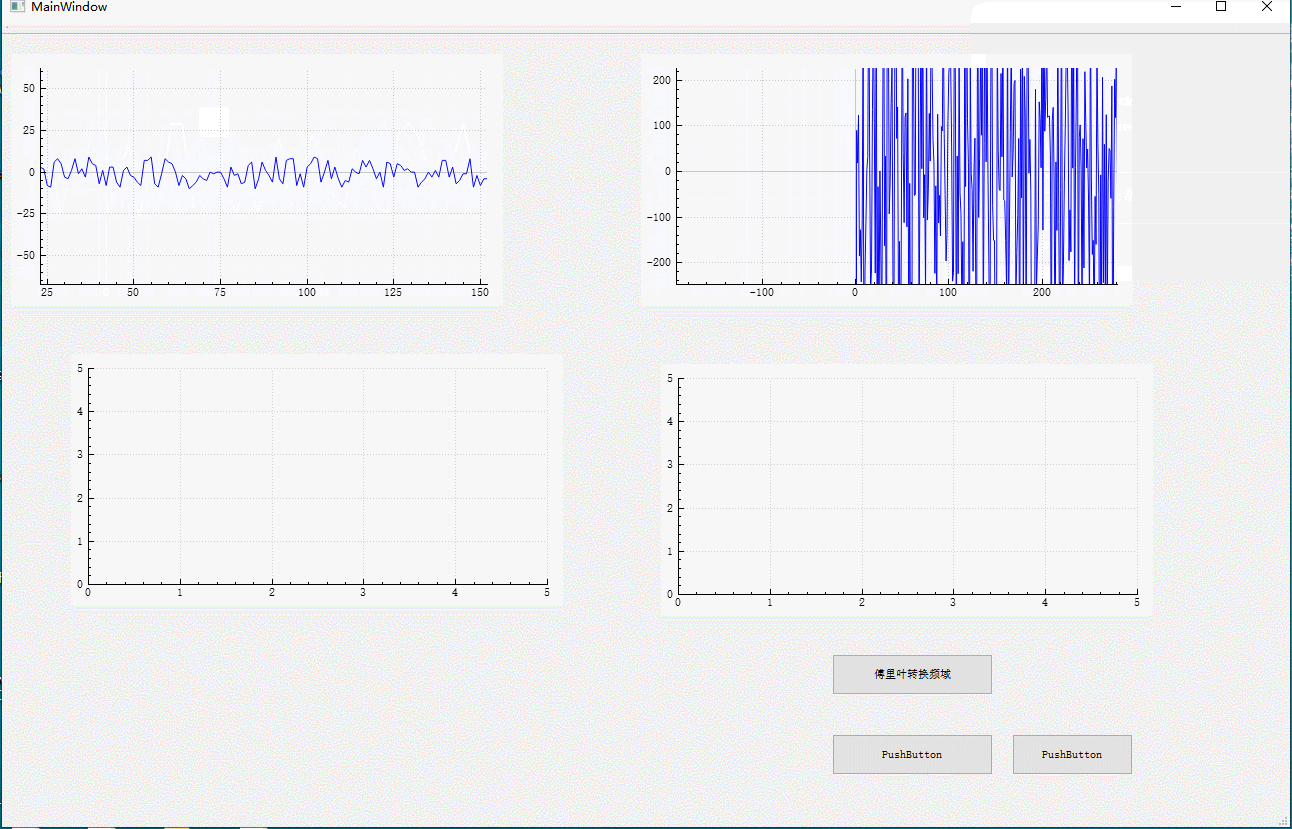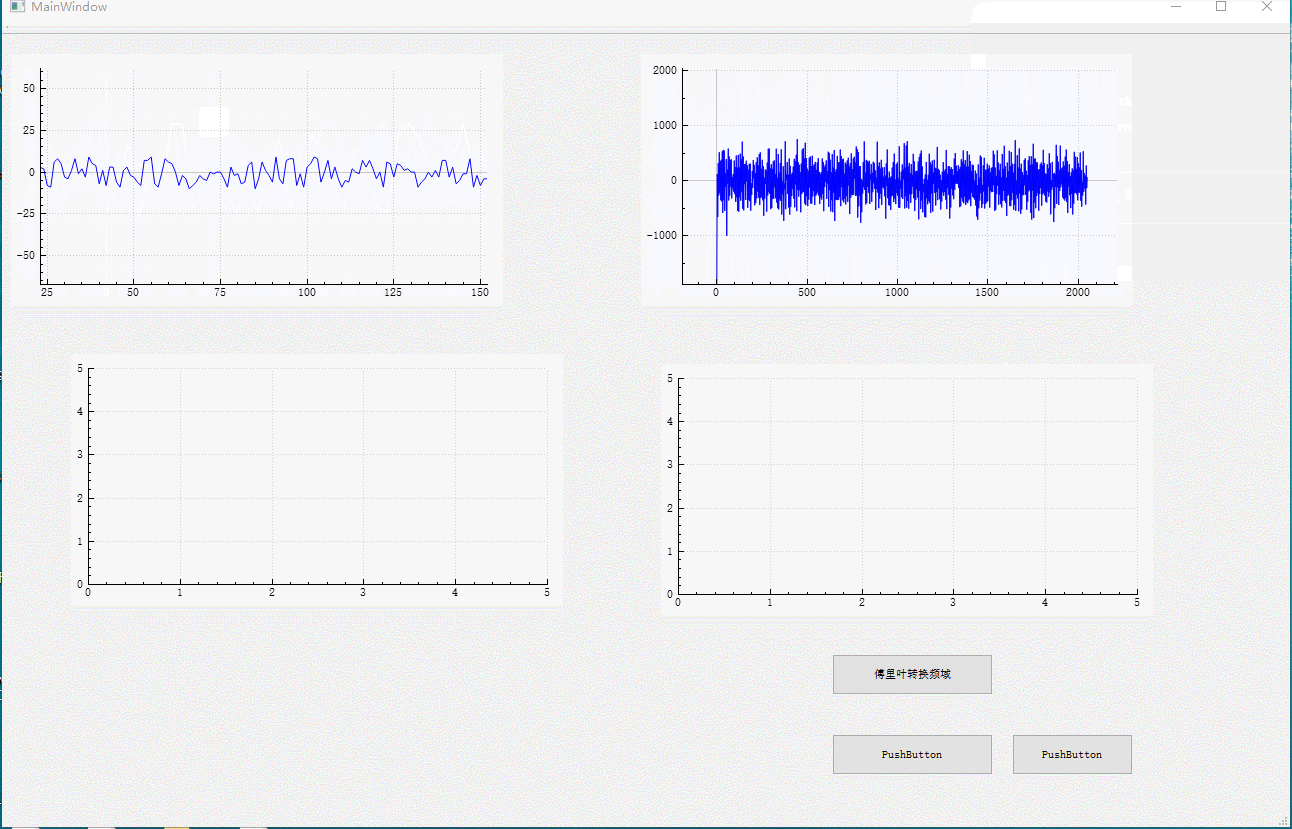
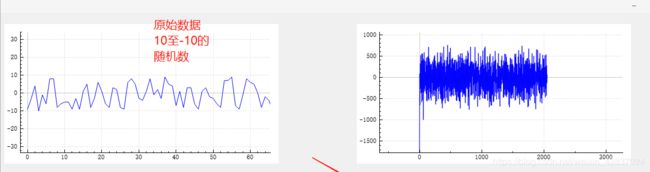
qt 傅里叶变换 fft 并画图(时域转换为频域)

前言:

这里我使用的 fft 类 是使用的这位博主的
https://blog.csdn.net/shadown1ght/article/details/77628389

我在上面封装一下 可以用qt的qvector 使用起来非常方便
把 fft.h 和 fft.cpp 添加进去，调用接口 传出时域数据,会返回频域数据

我这里使用的超强绘图控件是 QCustomplot
支持大量数据显示 500w 条都不卡顿 支持拖动 缩放等交互操作

我的原始数据也就是时域 是 4096个 -10 到 10的随机数

	QVector<double> x_,y_;

    for(auto i = 0; i<4096;i++)
    {
        x_<<i;
        y_<<qrand() % 20 - 10;
    }

fft类的使用

	fft* m_fft = new fft();
	

	/*
	*typedef struct Complex
	{
    double rl;              //实部 用这个当做y轴画图像就可以
    double im;              //虚部
	}Complex;
	**/

	//用上面的原始数据的初始化这个结构体类
	QVector<Complex> in_(x_.size());
    QVector<Complex> out_(x_.size());

    for(auto i = 0; i< x_.size();i++)
    {
        in_[i].rl = y_[i];
    }

	//调用接口 生成频域的 out_ 数据 
    m_fft->fft1(in_,in_.size(),out_);

    QVector<double> x1,y1;

    for(auto i = 0;i<out_.size()/2;i++)
    {
        x1<<i;
        //用计算出的实部当做y轴画图
        y1<<out_[i].rl;

    }

	//画图
    plot2->graph(0)->setData(x1,y1);
    plot2->replot();

fft 类的完整code

fft.h

#ifndef FFT_H
#define FFT_H

#include 
#include 
/*
*
*
*               计算傅里叶变换频谱
*
*
* */
#define      MAX_MATRIX_SIZE                4194304             // 2048 * 2048
#define      PI                             3.141592653
#define      MAX_VECTOR_LENGTH              10000


typedef struct Complex
{
    double rl;              //实部 用这个当做y轴画图像就可以
    double im;              //虚部
}Complex;
class fft : public QObject
{
    Q_OBJECT
public:
    explicit fft(QObject *parent = nullptr);
//   bool fft1(Complex  const inVec[], int  const len, Complex  outVec[]);
    //傅里叶转换 频域
    bool fft1(QVector<Complex>inVec, int  const len, QVector<Complex>&outVec);

    //逆转换
   bool ifft(Complex  const inVec[], int  const len, Complex  outVec[]);

   int get_computation_layers(int  num);

   bool is_power_of_two(int  num);

   void test();

signals:

public slots:
};

#endif // FFT_H

fft.cpp

#include "fft.h"
#include 
fft::fft(QObject *parent) : QObject(parent)
{

}

bool fft::fft1(QVector<Complex> inVec, const int len, QVector<Complex> &outVec)
{
    if ((len <= 0) || (inVec.isEmpty()) || ( outVec.isEmpty()))
        return false;
    if (!is_power_of_two(len))
        return false;

    qDebug()<<"come in";
    // create the weight array
    Complex         *pVec = new Complex[len];
    Complex         *Weights = new Complex[len];
    Complex         *X = new Complex[len];
    int                   *pnInvBits = new int[len];

    //memcpy(pVec, inVec, len*sizeof(Complex));

    for(int i = 0; i < len;i++)
    {
        pVec[i].im = inVec.at(i).im;
        pVec[i].rl = inVec.at(i).rl;
    }


    // 计算权重序列
    double fixed_factor = (-2 * PI) / len;
    for (int i = 0; i < len / 2; i++) {
        double angle = i * fixed_factor;
        Weights[i].rl = cos(angle);
        Weights[i].im = sin(angle);
    }
    for (int i = len / 2; i < len; i++) {
        Weights[i].rl = -(Weights[i - len / 2].rl);
        Weights[i].im = -(Weights[i - len / 2].im);
    }

    int r = get_computation_layers(len);

    // 计算倒序位码
    int index = 0;
    for (int i = 0; i < len; i++) {
        index = 0;
        for (int m = r - 1; m >= 0; m--) {
            index += (1 && (i & (1 << m))) << (r - m - 1);
        }
        pnInvBits[i] = index;
        X[i].rl = pVec[pnInvBits[i]].rl;
        X[i].im = pVec[pnInvBits[i]].im;
    }

    // 计算快速傅里叶变换
    for (int L = 1; L <= r; L++) {
        int distance = 1 << (L - 1);
        int W = 1 << (r - L);

        int B = len >> L;
        int N = len / B;

        for (int b = 0; b < B; b++) {
            int mid = b*N;
            for (int n = 0; n < N / 2; n++) {
                int index = n + mid;
                int dist = index + distance;
                pVec[index].rl = X[index].rl + (Weights[n*W].rl * X[dist].rl - Weights[n*W].im * X[dist].im);                      // Fe + W*Fo
                pVec[index].im = X[index].im + Weights[n*W].im * X[dist].rl + Weights[n*W].rl * X[dist].im;
            }
            for (int n = N / 2; n < N; n++) {
                int index = n + mid;
                pVec[index].rl = X[index - distance].rl + Weights[n*W].rl * X[index].rl - Weights[n*W].im * X[index].im;        // Fe - W*Fo
                pVec[index].im = X[index - distance].im + Weights[n*W].im * X[index].rl + Weights[n*W].rl * X[index].im;
            }
        }

//        memcpy(X, pVec, len*sizeof(Complex));

        for(int i = 0; i< len;i++)
        {
            X[i].im = pVec[i].im;
            X[i].rl = pVec[i].rl;
        }
    }

   // memcpy(outVec, pVec, len*sizeof(Complex));

    for(int i = 0; i < len;i++)
    {
        outVec[i].im = pVec[i].im;
        outVec[i].rl = pVec[i].rl;
    }



    if (Weights)      delete[] Weights;
    if (X)                 delete[] X;
    if (pnInvBits)    delete[] pnInvBits;
    if (pVec)           delete[] pVec;
    return true;
}

/*bool fft::fft1(const Complex inVec[], const int len, Complex outVec[])
{

    char msg[256] = "11111 ";

    if ((len <= 0) || (NULL == inVec) || (NULL == outVec))
        return false;
    if (!is_power_of_two(len))
        return false;

    // create the weight array
    Complex         *pVec = new Complex[len];
    Complex         *Weights = new Complex[len];
    Complex         *X = new Complex[len];
    int                   *pnInvBits = new int[len];

    memcpy(pVec, inVec, len*sizeof(Complex));

    // 计算权重序列
    double fixed_factor = (-2 * PI) / len;
    for (int i = 0; i < len / 2; i++) {
        double angle = i * fixed_factor;
        Weights[i].rl = cos(angle);
        Weights[i].im = sin(angle);
    }
    for (int i = len / 2; i < len; i++) {
        Weights[i].rl = -(Weights[i - len / 2].rl);
        Weights[i].im = -(Weights[i - len / 2].im);
    }

    int r = get_computation_layers(len);

    // 计算倒序位码
    int index = 0;
    for (int i = 0; i < len; i++) {
        index = 0;
        for (int m = r - 1; m >= 0; m--) {
            index += (1 && (i & (1 << m))) << (r - m - 1);
        }
        pnInvBits[i] = index;
        X[i].rl = pVec[pnInvBits[i]].rl;
        X[i].im = pVec[pnInvBits[i]].im;
    }

    // 计算快速傅里叶变换
    for (int L = 1; L <= r; L++) {
        int distance = 1 << (L - 1);
        int W = 1 << (r - L);

        int B = len >> L;
        int N = len / B;

        for (int b = 0; b < B; b++) {
            int mid = b*N;
            for (int n = 0; n < N / 2; n++) {
                int index = n + mid;
                int dist = index + distance;
                pVec[index].rl = X[index].rl + (Weights[n*W].rl * X[dist].rl - Weights[n*W].im * X[dist].im);                      // Fe + W*Fo
                pVec[index].im = X[index].im + Weights[n*W].im * X[dist].rl + Weights[n*W].rl * X[dist].im;
            }
            for (int n = N / 2; n < N; n++) {
                int index = n + mid;
                pVec[index].rl = X[index - distance].rl + Weights[n*W].rl * X[index].rl - Weights[n*W].im * X[index].im;        // Fe - W*Fo
                pVec[index].im = X[index - distance].im + Weights[n*W].im * X[index].rl + Weights[n*W].rl * X[index].im;
            }
        }

        memcpy(X, pVec, len*sizeof(Complex));
    }

    memcpy(outVec, pVec, len*sizeof(Complex));
    if (Weights)      delete[] Weights;
    if (X)                 delete[] X;
    if (pnInvBits)    delete[] pnInvBits;
    if (pVec)           delete[] pVec;
    return true;

}
*/
bool fft::ifft(const Complex inVec[], const int len, Complex outVec[])
{
    char msg[256] = "11111 ";

        if ((len <= 0) || (!inVec))
            return false;
        if (false == is_power_of_two(len)) {
            return false;
        }

        double         *W_rl = new double[len];
        double         *W_im = new double[len];
        double         *X_rl = new double[len];
        double         *X_im = new double[len];
        double         *X2_rl = new double[len];
        double         *X2_im = new double[len];

        double fixed_factor = (-2 * PI) / len;
        for (int i = 0; i < len / 2; i++) {
            double angle = i * fixed_factor;
            W_rl[i] = cos(angle);
            W_im[i] = sin(angle);
        }
        for (int i = len / 2; i < len; i++) {
            W_rl[i] = -(W_rl[i - len / 2]);
            W_im[i] = -(W_im[i - len / 2]);
        }

        // 时域数据写入X1
        for (int i = 0; i < len; i++) {
            X_rl[i] = inVec[i].rl;
            X_im[i] = inVec[i].im;
        }
        memset(X2_rl, 0, sizeof(double)*len);
        memset(X2_im, 0, sizeof(double)*len);

        int r = get_computation_layers(len);
        if (-1 == r)
            return false;
        for (int L = r; L >= 1; L--) {
            int distance = 1 << (L - 1);
            int W = 1 << (r - L);

            int B = len >> L;
            int N = len / B;
            //sprintf(msg + 6, "B %d, N %d, W %d, distance %d, L %d", B, N, W, distance, L);
            //OutputDebugStringA(msg);

            for (int b = 0; b < B; b++) {
                for (int n = 0; n < N / 2; n++) {
                    int index = n + b*N;
                    X2_rl[index] = (X_rl[index] + X_rl[index + distance]) / 2;
                    X2_im[index] = (X_im[index] + X_im[index + distance]) / 2;
                    //sprintf(msg + 6, "%d, %d: %lf, %lf", n + 1, index, X2_rl[index], X2_im[index]);
                    //OutputDebugStringA(msg);
                }
                for (int n = N / 2; n < N; n++) {
                    int index = n + b*N;
                    X2_rl[index] = (X_rl[index] - X_rl[index - distance]) / 2;           // 需要再除以W_rl[n*W]
                    X2_im[index] = (X_im[index] - X_im[index - distance]) / 2;
                    double square = W_rl[n*W] * W_rl[n*W] + W_im[n*W] * W_im[n*W];          // c^2+d^2
                    double part1 = X2_rl[index] * W_rl[n*W] + X2_im[index] * W_im[n*W];         // a*c+b*d
                    double part2 = X2_im[index] * W_rl[n*W] - X2_rl[index] * W_im[n*W];          // b*c-a*d
                    if (square > 0) {
                        X2_rl[index] = part1 / square;
                        X2_im[index] = part2 / square;
                    }
                }
            }
            memcpy(X_rl, X2_rl, sizeof(double)*len);
            memcpy(X_im, X2_im, sizeof(double)*len);
        }

        // 位码倒序
        int index = 0;
        for (int i = 0; i < len; i++) {
            index = 0;
            for (int m = r - 1; m >= 0; m--) {
                index += (1 && (i & (1 << m))) << (r - m - 1);
            }
            outVec[i].rl = X_rl[index];
            outVec[i].im = X_im[index];
            //sprintf(msg + 6, "X_rl[i]: %lf, %lf,  index: %d", out_rl[i], out_im[i], index);
            //OutputDebugStringA(msg);
        }

        if (W_rl)      delete[] W_rl;
        if (W_im)    delete[] W_im;
        if (X_rl)      delete[] X_rl;
        if (X_im)     delete[] X_im;
        if (X2_rl)     delete[] X2_rl;
        if (X2_im)    delete[] X2_im;

        return true;

}

int fft::get_computation_layers(int num)
{

    int nLayers = 0;
    int len = num;
    if (len == 2)
        return 1;
    while (true) {
        len = len / 2;
        nLayers++;
        if (len == 2)
            return nLayers + 1;
        if (len < 1)
            return -1;
    }

}

bool fft::is_power_of_two(int num)
{

    int temp = num;
    int mod = 0;
    int result = 0;

    if (num < 2)
        return false;
    if (num == 2)
        return true;

    while (temp > 1)
    {
        result = temp / 2;
        mod = temp % 2;
        if (mod)
            return false;
        if (2 == result)
            return true;
        temp = result;
    }
    return false;

}
/*
void fft::test()
{
    double vec[] = { 15, 32, 9, 222, 118, 151, 5, 7, 56, 233, 56, 121, 235, 89, 98, 111 };
    int len = sizeof(vec) / sizeof(double);

    Complex *inVec = new Complex[len];
    Complex *outVec = new Complex[len];
    Complex *invert = new Complex[len];

    memset(inVec, 0, len*sizeof(Complex));
    for (int i = 0; i < len; i++)
        inVec[i].rl = vec[i];

    // Fourier transformation
    fft1(inVec, len, outVec);

    // print result
    char msg[256] = "11111 ";
   // OutputDebugStringA("11111 快速傅里叶变换结果为：");
    qDebug()<<"快速傅里叶变换结果为：";
    for (int i = 0; i < len; i++) {
        if (outVec[i].im < 0)
            sprintf(msg + 6, "result[%d]: %lf - %lfi", i+1, outVec[i].rl, -outVec[i].im);
        else
            sprintf(msg + 6, "result[%d]: %lf + %lfi", i + 1, outVec[i].rl, outVec[i].im);
        //OutputDebugStringA(msg);
        qDebug()<

我只用这个接口就可以