小猪的数据结构辅助教程——3.3 栈的应用实例:逆波兰式(RPN)
小猪的数据结构辅助教程——3.3 栈的应用实例:逆波兰式(RPN)
标签(空格分隔): 数据结构
1.逆波兰式的概述
1)逆波兰式的引入:
在开始讲解逆波兰式之前,我们先来了解下我们平时数学里是如何写表达式的,比如:
8 * (1 + 2) / (2 + 4),好的,瞄一眼,我们就能得出结果是4,我们是根据运算符
的优先级来计算的,括号 > 乘除 > 加减,是吧!我们很简单就能得出结果,但是,假如
这上面的这段表达式丢给计算机呢?计算机需要进行多次if判断才能够决定先算哪一部分!
有没有什么好的解决方法呢?答案肯定是有的:比如本节要讲的逆波兰式~
2)逆波兰式的介绍:
逆波兰式,你也可以叫做:逆波兰表达式,可以理解成后缀表达式,我们平时数学写的
那种表达式叫中缀表达式,中缀后缀,其实就是运算符在表达式中的位置,比如上面的:
中缀表达式:8 * (1 + 2) / (2 + 4)
后缀表达式(逆波兰式):8 1 2 + 2 4 + / *
可能你对上面的后缀表达式不是很了解,没事,下面来看下如何利用栈,将中缀表示式
转换为后缀逆波兰式!
3)如何将中缀表达式转换为逆波兰式
我们以上面的:8 * (1 + 2) / (2 + 4)为例,我们用两个栈,一个用来存放中缀表达式的
每个元素,一个用来来存放转换过程中的操作符号!每次从栈中取出一个元素,做如下判断:
①数字,直接打印
②运算符(±*/),和操作符栈中的栈顶元素进行运算优先级的比较:
如果大于等于栈顶,将这个运算符入栈
否则弹出栈顶的运算符,打印,然后将新运算符压入栈中
③左括号,直接入栈
④右括号,弹出栈中的元素,直到遇到左括号!
好的,规则有了,下面我们来演示下这个过程:
- 8是数字,打印,此时打印的内容:8
- *****是运算符,压入栈中,此时栈{*};
- (,直接压入栈中,此时栈{*,(};
- 1是数字,打印,此时打印的内容:8 1
- **+**是运算符,压入栈中,此时栈{*,),+}
- 2是数字,打印,此时打印的内容:8 1 2
- ),弹出栈中的元素,直到遇到(,此时栈{*},此时打印的内容:8 1 2 +
- **/**是运算符,优先级和一样,压入栈中,此时栈{,/}
- (,直接压入栈中,此时栈{*,/,(}
- 2是数字,打印,此时打印的内容:8 1 2 + 2
- **+**是运算符,压入栈中,此时栈{*,/,(,+}
- 4是数字,打印,此时打印的内容:8 1 2 + 2 4
- ),弹出栈中的元素,直到遇到(,此时栈{*,/},此时打印的内容:8 1 2 + 2 4 +
- 将栈中剩余的元素弹出,此时打印的内容:**8 1 2 + 2 4 + / ***
好的,演示到这里,相信你对逆波兰式应该基本了解了,下面该准备动手写代码了,本节
我们来写两个程序,中缀表达式转成逆波兰式和逆波兰式的结果计算!
2.中缀表达式转成逆波兰式的代码实现:
运行截图:
代码实现:
#include
#define STACK_INIT_SIZE 10 //存储空间的初始分配量
#define STACK_INCREMENT 2 //分配增量
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef char SElemType;
typedef int Status;
typedef struct SqStack
{
SElemType *base; //栈底指针变量
SElemType *top; //栈顶指针变量
int stacksize; //当前可试用的最大容量
}SqStack;
//初始化栈
void InitStack(SqStack *S)
{
S->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
if( !S->base)exit(0);
S->top = S->base;
S->stacksize = STACK_INIT_SIZE;
}
//入栈
void PushStack(SqStack *S, SElemType e)
{
if(S->top - S->base >= S->stacksize )
{
S->base = (SElemType *)realloc(S->base, (S->stacksize + STACK_INCREMENT) * sizeof(SElemType));
if( !S->base )exit(0);
S->top = S->base + S->stacksize;
S->stacksize = S->stacksize + STACK_INCREMENT;
}
*(S->top) = e;
S->top++;
}
//出栈
void PopStack(SqStack *S, SElemType *e)
{
if(S->top == S->base )return;
*e = *--(S->top);
}
//获取栈的当前长度
int StackLength(SqStack S)
{
return (S.top - S.base);
}
int main()
{
SqStack s;
char c,e;
InitStack(&s);
printf("请输入中缀表达式,以#作为结束标记:\n");
scanf("%c",&c);
printf("输出转换后的逆波兰式:\n");
while(c != '#')
{
//这里需要考虑数字会是多位的情况
while(c >= '0' && c <= '9')
{
printf("%c", c);
scanf("%c", &c);
if( c<'0' || c>'9' )
{
printf(" ");
}
}
//假如是右括号,弹出栈中的字符,直到遇到左括号
if( ')' == c )
{
PopStack(&s, &e);
while( '(' != e )
{
printf("%c ", e);
PopStack(&s, &e);
}
}
//假如是加减号 ,如果栈里没元素,直接压栈,有要做下判断
else if( '+'==c || '-'==c )
{
if( !StackLength(s) )
{
PushStack(&s, c);
}
else
{
do
{
PopStack(&s, &e);
if( '(' == e )
{
PushStack(&s, e);
}
else
{
printf("%c ", e);
}
}while( StackLength(s) && '('!=e );
PushStack(&s, c);
}
}
//假如是乘除或左括号,直接压栈
else if( '*'==c || '/'==c || '('==c )
{
PushStack(&s, c);
}
//是#,则代表表达式输入完毕
else if( '#'== c )
{
break;
}
//如果是其他字符,打印字符不合法
else
{
printf("\n出错:输入错误!\n");
return -1;
}
scanf("%c", &c);
}
//遍历栈中的剩余运算符
while( StackLength(s))
{
PopStack(&s, &e);
printf("%c ", e);
}
printf("\n\n");
return 0;
}
代码直接看main部分的就可以了,写了很详细的注释,应该能看懂,逻辑
很简单,无非是判断,然后入栈出栈打印而已,另外,吐槽下,不习惯C写{}的风格…

3.逆波兰式的结果计算
这里用到两个个函数:
- int isdigit(char c):
ctype.h库为我们提供的用于检查参数c是否为阿拉伯数字0到9的函数!
- double atof(const char *nptr);
stdlib.h库给我们提供的把字符串转换成浮点数的函数
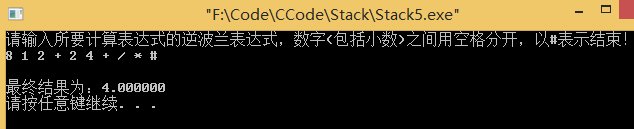
运行截图:
代码实现:
#include
#include
#include
#define STACK_INIT_SIZE 10 //存储空间的初始分配量
#define STACK_INCREMENT 2 //分配增量
#define MAX_BUFFER_SIZE 10
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef double SElemType;
typedef int Status;
typedef struct SqStack
{
SElemType *base; //栈底指针变量
SElemType *top; //栈顶指针变量
int stacksize; //当前可试用的最大容量
}SqStack;
//初始化栈
void InitStack(SqStack *S)
{
S->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
if( !S->base)exit(0);
S->top = S->base;
S->stacksize = STACK_INIT_SIZE;
}
//入栈
void PushStack(SqStack *S, SElemType e)
{
if(S->top - S->base >= S->stacksize )
{
S->base = (SElemType *)realloc(S->base, (S->stacksize + STACK_INCREMENT) * sizeof(SElemType));
if( !S->base )exit(0);
S->top = S->base + S->stacksize;
S->stacksize = S->stacksize + STACK_INCREMENT;
}
*(S->top) = e;
S->top++;
}
//出栈
void PopStack(SqStack *S, SElemType *e)
{
if(S->top == S->base )return;
*e = *--(S->top);
}
//获取栈的当前长度
int StackLength(SqStack S)
{
return (S.top - S.base);
}
//判断是否为空栈
Status StackEmpty(SqStack S)
{
return S.top == S.base?TRUE:FALSE;
}
int main()
{
char c;
double d,e;
int i = 0;
char buffer[MAX_BUFFER_SIZE];
SqStack s;
InitStack(&s);
printf("请输入所要计算表达式的逆波兰表达式,数字(包括小数)之间用空格分开,以#表示结束!\n");
scanf("%c",&c);
while(c!='#')
{
//判断字符是否为数字或小数点
while(isdigit(c)||c=='.')
{
buffer[i++]=c;
buffer[i]='\0';
if(i>=10){
printf("\n出错!超过最大缓冲区大小!\n");
return -1;
}
scanf("%c",&c);
//判断是否为空格,是的话将缓冲区里的字符串转换为double类型的数据,压入栈中
if(c == ' ')
{
d = atof(buffer);
PushStack(&s,d);
i=0;
break;
}
}
//如果是运算符则,弹出栈中的两个元素,作为参数进行运算,将结果压入栈中
//另外,要注意:除法除数不能为0
switch(c)
{
case '+':
PopStack(&s,&d);
PopStack(&s,&e);
PushStack(&s,d+e);
break;
case '-':
PopStack(&s,&d);
PopStack(&s,&e);
PushStack(&s,e-d);
break;
case '*':
PopStack(&s,&d);
PopStack(&s,&e);
PushStack(&s,d*e);
break;
case '/':
PopStack(&s,&d);
PopStack(&s,&e);
if(e!=0)PushStack(&s,e/d);
else{
printf("\n出错,除数不能为0!");
return -1;
}
break;
}
scanf("%c",&c);
}
PopStack(&s,&d);
printf("\n最终结果为:%f\n",d);
return 0;
}
和上面一样,写了很详细的注释,代码应该都能看懂~
上述两个程序参考自——小甲鱼的《数据结构与算法教学》系列!
4.本节示例代码下载:
https://github.com/coder-pig/Data-structure-auxiliary-tutorial/blob/master/Stack/Stack4.c
https://github.com/coder-pig/Data-structure-auxiliary-tutorial/blob/master/Stack/Stack5.c