leetcode【数据结构简介】《数组和字符串》卡片——二维数组简介

Authur Whywait 做一块努力吸收知识的海绵
想看博主的其他所有leetcode卡片学习笔记链接？传送门点这儿

二维数组简介

类似于一维数组，二维数组也是由元素的序列组成。但是这些元素可以排列在矩形网格中而不是直线上。

原理

在一些语言中，多维数组实际上是在内部作为一维数组实现的，而在其他一些语言中，实际上根本没有多维数组。
比如：

C++ 将二维数组存储为一维数组。
下图显示了大小为 M * N 的数组 A 的实际结构：

A[0][0]	…	A[0][N-1]	A[1][0]	…	A[1][N-1]	…	A[M-1][0]	…	A[M-1][N-1]

因此，如果我们将 A 定义为也包含 M * N 个元素的一维数组，那么实际上 A[i][j] 就等于 A[i * N + j]。

动态二维数组

可以用与一维动态数组类似的方法定义动态二维数组。
实际上，它可以只是一个嵌套的动态数组。传送至：一维动态数组

编程练习

1.对角线遍历

题目

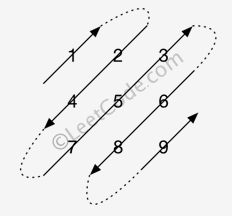
给定一个含有 M x N 个元素的矩阵（M 行，N 列），请以对角线遍历的顺序返回这个矩阵中的所有元素，对角线遍历如下图所示。

测试用例

输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,4,7,5,3,6,8,9]

思路

• while循环至矩阵的最后一个元素。每一次循环把一个矩阵中的值拿出来丢到一个辅助的线性数组里面。
• 循环体里面主要分为6种情况：
  1. 上沿，行列之和为偶数
  2. 下沿，行列之和为奇数
  3. 左沿，行列之和为奇数
  4. 右沿，行列之和为偶数
  5. 除1-4之外的行列之和为奇数
  6. 除1-4之外的行列之和为偶数

犯过的错

问题一：while循环的条件

while(i!=matrixSize-1 && j!=matrixColSize-1)；

乍一看没啥错误。但是仔细一想确是不行。
简单暴力的反例灵魂质问：如果i=matrixSize-1,j=1的时候要跳出循环吗？
所以应该改成以下两种：

while(i!=matrixSize-1 || j!=matrixColSize-1)；

while(!(i==matrixSize-1 && j==*matrixColSize-1))；

问题二：特例的考虑与判断

如果输入为[]，输出也应为[];
此处特例判断时，故需要写在最前面。

if(matrixSize==0 || (*matrixColSize==0 || (* returnSize==0))){     
	* returnSize = 0;    
	return NULL;
}

但是遇到[[1]]的测试用例时，尽管在自己的控制台里可以运行正确结果[1]，但是在提交之后却是有很大问题[1](下面的程序都是正确的)。但是在尝试之后，我将上面代码换为

if(matrixSize==0){    
	* returnSize = 0;    	
	return NULL;
}

问题就解决了。
问题二关乎变量的初始化以及赋值问题问题。

代码

int* findDiagonalOrder(int** matrix, int matrixSize, int* matrixColSize, int* returnSize){        
	if(matrixSize==0){        
	* returnSize = 0;        
	return NULL;    
	}
	* returnSize = matrixSize * (* matrixColSize);
	int* array = (int *)malloc(sizeof(int) * (* returnSize));
	int position=0; int i=0, j=0;

	while(!(i==matrixSize-1 && j==(*matrixColSize)-1) && i+1 && j+1 && matrixSize && * matrixColSize){                
		array[position++] = matrix[i][j];                
		if(!j && i<matrixSize-1 && (i+j)%2) i++;        
		else if(i==matrixSize-1 && j<*matrixColSize-1 && (i+j)%2) j++;        
		else if(!i && j<*matrixColSize-1 && !((i+j)%2)) j++;         
		else if(j==(*matrixColSize)-1 && i<matrixSize-1 && !((i+j)%2)) i++;         
		else if((i+j)%2){            
			i++;j--;        
		}        
		else if(!((i+j)%2)){            
			i--;j++;        
		}        
		else puts("something is wrong!");            
	}

	array[position] = matrix[i][j];    
	return array;
}

运行效果

2. 螺旋矩阵

题目

给定一个包含 m x n 个元素的矩阵（m 行, n 列），请按照顺时针螺旋顺序，返回矩阵中的所有元素。

测试用例

输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,3,6,9,8,7,4,5]

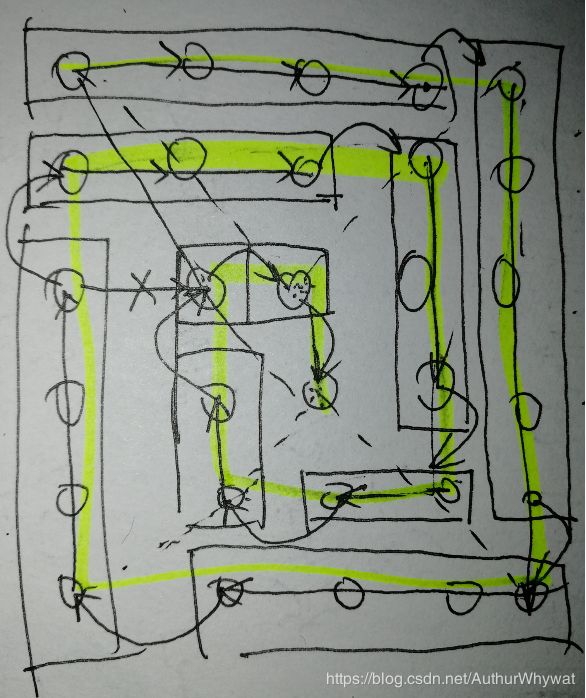
思路

其实开始的时候是尝试另一种方法：通过i和j两个位置坐标的相对关系，然后判断坐标位置属于哪一个阵营(阵营一共有四个：右移阵营，下移阵营，左移阵营，上移阵营)。不过这种方法又是ceil函数又是floor函数，四个阵营的判断，每个需要两到三个约束条件，实在让人苦不言堪。

算着算着，脑子里就蹦出来了另一个想法：每次转弯的个数都减一，何不直接拿来作为思路，既不需要苦苦计算条件，也不用执行算一堆表达式，直接清清爽爽“肠道通畅”地一条捋下来，岂不是很爽？于是就一个backspace，把前面写了大半的代码全删了。果然，程序跑得又快又好！(此处忽略亿点debug细节。)
【注】使用“肠道通畅”方法的在判断属于何种阵营方面使用了flag变量，对4取余之后不就只有四个值然后就分别对应四个阵营了么~

代码

int* spiralOrder(int** matrix, int matrixSize, int* matrixColSize, int* returnSize){
    if(!matrixSize){        
    * returnSize = 0;        
    return NULL;    
    }
    * returnSize = matrixSize * (* matrixColSize);    
    int *array = (int *)malloc(sizeof(int) * (*returnSize));    
    int position=0, i=0, j=0, flag=0;    
    int m=matrixSize-1, n=*matrixColSize-1;
    
    for(int k=0; k<n; k++) array[position++] = matrix[i][j++];    
    flag++;
    while(position < *returnSize - 1){
    	if(!flag){            
    	    for(int k=0; k<n; k++) array[position++] = matrix[i][j++];
    	    n--;            
    	    flag = (flag+1)%4; 
    	}
	else if(flag == 1){            
	    for(int k=0; k<m; k++) array[position++] = matrix[i++][j];            
	    m--;            
	    flag = (flag+1)%4;        
	}
	else if(flag == 2){            
	    for(int k=0; k<n; k++) array[position++] = matrix[i][j--];            
	    n--;            
	    flag = (flag+1)%4;        
	}
	else if(flag == 3){            
	    for(int k=0; k<m; k++) array[position++] = matrix[i--][j];            
	    m--;            
	    flag = (flag+1)%4;        
	}else;
    }
    array[position] = matrix[i][j];
    return array;
}

运行效果

3. 杨辉三角

题目

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

测试用例

输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]

思路

比较简单就不赘述了

tri[i][j] = tri[i-1][j-1] + tri[i-1][j];

涉及要点

二维动态数组，数组每一行分配的空间不一定是一样的，可以按照实际每行依次分配空间。

先给每行分配一个空间，然后再给每行的空间分别分配一个长度相同的空间。对于本题，具体操作如下：

首先要明确，需要给* returnColumnSizes分配长度为sizeof(int) * numRows的空间。
目的：构建一个空间，为后面每个数组的长度的存储做储备
代码如下：

* returnColumnSizes = (int*)malloc(sizeof(int) * numRows);

然后给定每一行存储的实际长度，进行赋值操作；

(*returnColumnSizes)[i] = i + 1;

得到了每行的数据长度之后，然后就要往自己新建的二维数组 tri 里面里头，塞数据，不过在此之前，需要分配空间，分配完空间之后就可以往里头塞东西。代码实现会在整体中实现。

代码

int** generate(int numRows, int* returnSize, int** returnColumnSizes){
    * returnSize = numRows;     
    * returnColumnSizes = (int*)malloc(sizeof(int) * numRows);    
    int **tri = (int **)malloc(sizeof(int *) * numRows);
    int i=0;    
    for(; i<*returnSize; i++){        
        (*returnColumnSizes)[i] = i + 1;        
        tri[i] = (int*)malloc((*returnColumnSizes)[i] * sizeof(int));        
        tri[i][0] = 1;        
        tri[i][i] = 1;    
    }
    for(i=2; i<numRows; i++){        
        for(int j=1; j<i; j++){            
            tri[i][j] = tri[i-1][j-1] + tri[i-1][j];        
        }    
    }    
    return tri;
}

执行效果

感想：
对于双指针还是不是很熟悉，后期多多研习。