第七章 网络优化与正则化
第七章 网络优化与正则化
- 第七章 网络优化与正则化
- 网络优化
- 网格优化的难点
- 网络结构多样性
- 高维变量的非凸优化
- 优化算法
- 小批量梯度下降
- 批量大小选择
- 学习率调整
- 学习率衰减
- 学习率预热
- 周期性学习率调整
- AdaGrad 算法
- RMSprop 算法
- AdaDelta 算法
- 梯度估计修正
- 动量法
- Nesterov 加速梯度
- Adam 算法
- 梯度截断
- 优化算法小结
- 参数初始化
- Xavier 初始化
- He 初始化
- 数据预处理
- 逐层归一化
- 批量归一化
- 层归一化
- 其它归一化方法
- 权重归一化
- 局部响应归一化
- 超参数优化
- 网格搜索
- 随机搜索
- 贝叶斯优化
- 动态资源分配
- 神经架构搜索
- 网络正则化
- L1和L2正则化
- 权重衰减
- 提前停止
- 丢弃法
- 循环神经网络上的丢弃法
- 数据增强
- 标签平滑
- 总结
第七章 网络优化与正则化
虽然神经网络具有非常强的表达能力,但是当应用神经网络模型到机器学 习时依然存在一些难点问题。主要分为两大类:
(1)优化问题:神经网络模型是一个非凸函数,再加上在深度网络中的梯度 消失问题,很难进行优化;另外,深度神经网络模型一般参数比较多,训练数据也 比较大,会导致训练的效率比较低。
(2)泛化问题:因为神经网络的拟合能力强,反而容易在训练集上产生过拟 合。因此在训练深度神经网络时,同时也需要通过一定的正则化方法来改进网络 的泛化能力。
目前,研究者从大量的实践中总结了一些经验技巧,从优化和正则化两个方 面来提高学习效率并得到一个好的网络模型。
网络优化
深度神经网络是一个高度非线性的模型,其风险函数是一个非凸函数,因此风险最小化是一个非凸优化问题,会存在很多局部最优点。
网格优化的难点
有效地学习深度神经网络的参数是一个具有挑战性的问题,其主要原因有 以下几个方面。
网络结构多样性
神经网络的种类非常多,比如卷积网络、循环网络等,其结构也非常不同。有 些比较深,有些比较宽。不同参数在网络中的作用也有很大的差异,比如连接权 重和偏置的不同,以及循环网络中循环连接上的权重和其它权重的不同。
由于网络结构的多样性,我们很难找到一种通用的优化方法。不同的优化方 法在不同网络结构上的差异也都比较大。
此外,网络的超参数一般也比较多,这也给优化带来很大的挑战。
高维变量的非凸优化
低维空间的非凸优化问题主要是存在一些局部最优点。基于梯度下降的优 化方法会陷入局部最优点,因此低维空间非凸优化的主要难点是如何选择初始 化参数和逃离局部最优点。深度神经网络的参数非常多,其参数学习是在非常高 维空间中的非凸优化问题,其挑战和在低维空间的非凸优化问题有所不同。
目前,深度神经网络的参数学习主要是通过梯度下降法来寻找一组可以最 小化结构风险的参数。在具体实现中,梯度下降法可以分为:批量梯度下降、随机梯度下降以及小批量梯度下降三种形式。根据不同的数据量和参数量,可以选择 一种具体的实现形式。
除了在收敛效果和效率上的差异,这三种方法都存在一些共同的问题,比如 1)如何改进优化算法;2)如何初始化参数;3)如何预处理数据等。
优化算法
小批量梯度下降
在训练深度神经网络时,训练数据的规模通常都比较大。如果在梯度下降
时,每次迭代都要计算整个训练数据上的梯度,这就需要比较多的计算资源。另外大规模训练集中的数据通常会非常冗余,也没有必要在整个训练集上计算梯 度。因此,在训练深度神经网络时,经常使用小批量梯度下降法(Mini-Batch Gradient Descent)。
批量大小选择
在小批量梯度下降法中,批量大小(Batch Size)对网络优化的影响也非常 大。一般而言,批量大小不影响随机梯度的期望,但是会影响随机梯度的方差。批量大小越大,随机梯度的方差越小,引入的噪声也越小,训练也越稳定,因此可以设置较大的学习率。
而批量大小较小时,需要设置较小的学习率,否则模型会不收敛。学习率通常要随着批量大小的增大而相应地增大。
一个简单有效的方法是线性缩放规则(Linear Scaling Rule)[Goyal等人,2017]:当批量大小增加m倍时,学习率也增加 m 倍。线性缩放规则往往在批量大小比较小时适用,当批量大小非常大时,线性缩放会使得训练不稳定。
学习率调整
学习率是神经网络优化时的重要超参数。在梯度下降法中,学习率 α 的取值 非常关键,如果过大就不会收敛,如果过小则收敛速度太慢。常用的学习率调整 方法包括学习率衰减、学习率预热、周期性学习率调整以及一些自适应调整学习 率的方法,比如 AdaGrad、RMSprop、AdaDelta 等。自适应学习率方法可以针对 每个参数设置不同的学习率。
学习率衰减
学习率预热
周期性学习率调整
为了使得梯度下降法能够逃离局部最小值或鞍点,一种经验性的方式是在 训练过程中周期性地增大学习率。虽然增大学习率可能短期内有损网络的收敛 稳定性,但从长期来看有助于找到更好的局部最优解。一般而言,当一个模型收敛一个平坦(Flat)的局部最小值时,其鲁棒性会更好,即微小的参数变动不会剧 烈影响模型能力;而当模型收敛到一个尖锐(Sharp)的局部最小值时,其鲁棒性也会比较差。具备良好泛化能力的模型通常应该是鲁棒的,因此理想的局部最小 值应该是平坦的。周期性学习率调整可以使得梯度下降法在优化过程中跳出尖锐的局部极小值,虽然会短期内会损害优化过程,但最终会收敛到更加理想的局部极小值。
本节介绍两种常用的周期性调整学习率的方法:循环学习率和带热重启的随机梯度下降。

AdaGrad 算法
RMSprop 算法
AdaDelta 算法
梯度估计修正
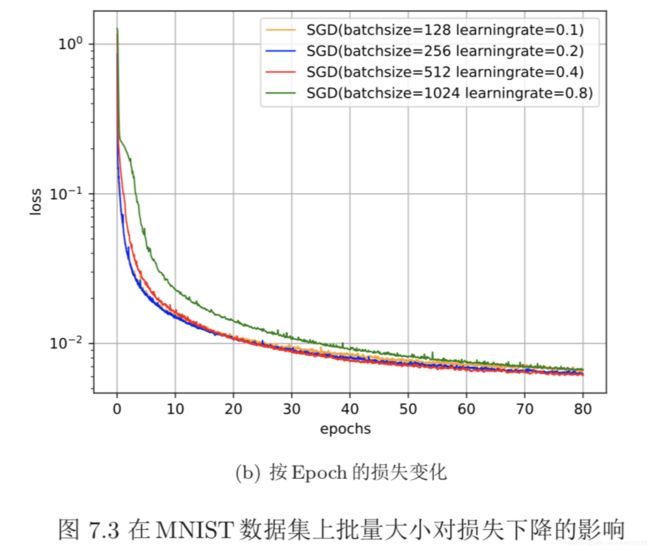
除了调整学习率之外,还可以进行梯度估计(Gradient Estimation)的修正。 从图7.3看出,在随机(小批量)梯度下降法中,如果每次选取样本数量比较小,损 失会呈现震荡的方式下降。也就是说,随机梯度下降方法中每次迭代的梯度估计 和整个训练集上的最优梯度并不一致,具有一定的随机性。一种有效地缓解梯度 估计随机性的方式是通过使用最近一段时间内的平均梯度来代替当前时刻的随 机梯度来作为参数更新的方向,从而提高优化速度。
动量法
Nesterov 加速梯度
Adam 算法
自适应动量估计(Adaptive Moment Estimation,Adam)算法[Kingma等 人,2015] 可以看作是动量法和 RMSprop 算法的结合,不但使用动量作为参数更 新方向,而且可以自适应调整学习率。
梯度截断
在深度神经网络或循环神经网络中,除了梯度消失之外,梯度爆炸也是影响学习效率的主要因素。在基于梯度下降的优化过程中,如果梯度突然增大,用大 的梯度更新参数反而会导致其远离最优点。为了避免这种情况,当梯度的模大于 一定阈值时,就对梯度进行截断,称为梯度截断(Gradient Clipping)[Pascanu等 人,2013]。

梯度截断是一种比较简单的启发式方法,把梯度的模限定在一个区间,当梯 度的模小于或大于这个区间时就进行截断。一般截断的方式有以下几种:
优化算法小结
参数初始化
神经网络训练过程中的参数学习是基于梯度下降法进行优化的。梯度下降法需要在开始训练时给每一个参数赋一个初始值。这个初始值的选取十分关键。
在感知器和 logistic 回归的训练中,我们一般将参数全部初始化为 0。但是这在神 经网络的训练中会存在一些问题。因为如果参数都为 0,在第一遍前向计算时,所 有的隐层神经元的激活值都相同。这样会导致深层神经元没有区分性。这种现象 也称为对称权重现象。
为了打破这个平衡,比较好的方式是对每个参数都随机初始化,这样使得不 同神经元之间的区分性更好。
随机初始化参数的一个问题是如何选取随机初始化的区间。如果参数取的太小,一是会导致神经元的输入过小,经过多层之后信号就慢慢消失了;二是还 会使得 Sigmoid 型激活函数丢失非线性的能力。以 Logistic 函数为例,在 0 附近 基本上是近似线性的。这样多层神经网络的优势也就不存在了。如果参数取的太大,会导致输入状态过大。对于 Sigmoid 型激活函数来说,激活值变得饱和,从而导致梯度接近于 0。
因此,要高效地训练神经网络,给参数选取一个合适的随机初始化区间是非 常重要的。一般而言,参数初始化的区间应该根据神经元的性质进行差异化的 设置。如果一个神经元的输入连接很多,它的每个输入连接上的权重就应该小一 些,以避免神经元的输出过大(当激活函数为 ReLU 时)或过饱和(当激活函数为 Sigmoid 函数时)。
经常使用的初始化方法有以下两种:
Xavier 初始化
He 初始化
数据预处理
逐层归一化
在深度神经网络中,中间某一层的输入是其之前的神经层的输出。因此,其 之前的神经层的参数变化会导致其输入的分布发生较大的差异。在使用随机梯 度下降来训练网络时,每次参数更新都会导致网络中间每一层的输入的分布发 生改变。越深的层,其输入的分布会改变得越明显。就像一栋高楼,低楼层发生一 个较小的偏移,都会导致高楼层较大的偏移。
从机器学习角度来看,如果某个神经层的输入分布发生了改变,那么其参数 需要重新学习,这种现象叫做内部协变量偏移(Internal Covariate Shift)。
批量归一化
层归一化
其它归一化方法
权重归一化
局部响应归一化
超参数优化
在神经网络中,除了可学习的参数之外,还存在很多超参数。这些超参数对 网络性能的影响也很大。不同的机器学习任务往往需要不同的超参数。常见的超参数有以下三类:
• 网络结构,包括神经元之间的连接关系、层数、每层的神经元数量、激活函 数的类型等。
• 优化参数,包括优化方法、学习率、小批量的样本数量等。
• 正则化系数。
超参数优化(Hyperparameter Optimization)主要存在两方面的困难。
(1) 超参数优化是一个组合优化问题,无法像一般参数那样通过梯度下降方法来优化,也没有一种通用有效的优化方法。
(2)评估一组超参数配置(Configuration) 的时间代价非常高,从而导致一些优化方法(比如演化算法(Evolution Algo- rithm)在超参数优化中难以应用。
网格搜索
随机搜索
贝叶斯优化
动态资源分配
在超参数优化中,每组超参数配置的评估代价比较高。如果我们可以在较早 的阶段就估计出一组配置的效果会比较差,那么我们就可以中止这组配置的评 估,将更多的资源留给其它配置。这个问题可以归结为多臂赌博机问题的一个泛 化问题:最优臂问题(Best-Arm Problem),即在给定有限的机会次数下,如何玩这些赌博机并找到收益最大的臂。和多臂赌博机问题类似,最优臂问题也是在利用和探索之间找到最佳的平衡。
由于目前神经网络的优化方法一般都采取随机梯度下降,因此我们可以通 过一组超参数的学习曲线来预估这组超参数配置是否有希望得到比较好的结 果。如果一组超参数配置的学习曲线不收敛或者收敛比较差,我们可以应用早期停止(Early-Stopping)策略来中止当前的训练。
神经架构搜索
上面介绍的超参数优化方法都是在固定(或变化比较小)的超参数空间X 中进行最优配置搜索,而最重要的神经网络架构一般还是需要由有经验的专家 来进行设计。从某种角度来讲,深度学习使得机器学习中的“特征工程”问题转变为“网络架构工程”问题。
神经架构搜索(Neural Architecture Search,NAS)[Zoph等人,2017]是一个 新的比较有前景的研究方向,通过神经网络来自动实现网络架构的设计。一个神 经网络的架构可以用一个变长的字符串来描述。利用元学习的思想,神经架构搜 索利用一个控制器来生成另一个子网络的架构描述。控制器可以由一个循环神 经网络来实现。控制器的训练可以通过强化学习来完成,其奖励信号为生成的子网络在开发集上的准确率。
网络正则化
机器学习模型的关键是泛化问题,即在样本真实分布上的期望风险最小化。 而训练数据集上的经验风险最小化和期望风险并不一致。由于神经网络的拟合 能力非常强,其在训练数据上的错误率往往都可以降到非常低,甚至可以到 0,从 而导致过拟合。因此,如何提高神经网络的泛化能力反而成为影响模型能力的最关键因素。
正则化(Regularization)是一类通过限制模型复杂度,从而避免过拟合,提 高泛化能力的方法,比如引入约束、增加先验、提前停止等。
L1和L2正则化
权重衰减
提前停止
丢弃法
集成学习的解释 每做一次丢弃,相当于从原始的网络中采样得到一个子网络。 如果一个神经网络有 n 个神经元,那么总共可以采样出 2n 个子网络。每次迭代都相当于训练一个不同的子网络,这些子网络都共享原始网络的参数。那么,最终 的网络可以近似看作是集成了指数级个不同网络的组合模型。
循环神经网络上的丢弃法
当在循环神经网络上应用丢弃法时,不能直接对每个时刻的隐状态进行随 机丢弃,这样会损害循环网络在时间维度上的记忆能力。一种简单的方法是对 非时间维度的连接(即非循环连接)进行随机丢失 [Zaremba 等人,2014]。如 图7.13所示,虚线边表示进行随机丢弃,不同的颜色表示不同的丢弃掩码。

然而根据贝叶斯学习的解释,丢弃法是一种对参数 θ 的采样。每次采样的参 数需要在每个时刻保持不变。因此,在对循环神经网络上使用丢弃法时,需要对 参数矩阵的每个元素进行随机丢弃,并在所有时刻都使用相同的丢弃掩码。这种 方法称为变分丢弃法(Variational Dropout)[Gal等人,2016b]。图7.14给出了变 分丢弃法的示例,相同颜色表示使用相同的丢弃掩码。

数据增强
标签平滑
总结
深度神经网络的优化和正则化是即对立又统一的关系。一方面我们希望优 化算法能找到一个全局最优解(或较好的局部最优解),另一方面我们又不希望 模型优化到最优解,这可能陷入过拟合。优化和正则化的统一目标是期望风险最小化。
在传统的机器学习中,有一些很好的理论可以帮助我们在模型的表示能力、 复杂度和泛化能力之间找到比较好的平衡,比如 Vapnik-Chervonenkis(VC)维 [Vapnik,1998] 和 Rademacher 复杂度 [Bartlett 等人,2002]。但是这些理论无法解 释深层神经网络在实际应用中的泛化能力表现。目前,深度神经网络的泛化能力还没有很好的理论支持。在传统机器学习模型上比较有效的 l1 或 l2 正则化在深 度神经网络中作用也比较有限,而一些经验的做法,比如使用随机梯度下降和提 前停止,会更有效。
根据通用近似定理,神经网络的表示能力十分强大。从直觉上,深度神经 网络很容易产生过拟合现象,因为增加的抽象层使得模型能够对训练数据中较 为罕见的依赖关系进行建模 [Bengio 等人,2013]。一些实验表明,虽然深层神 经网络的容量足够记住所有训练数据,但依然优先记住训练数据中的一般模式(Pattern),即高泛化能力的模式 [Zhang 等人,2016]。
近年来深度学习的快速发展在一定程度上也归因于很多深度神经网络的优 化和正则化方法的出现。虽然这些方法往往是经验性的,但在实践中取得了很好 的效果,使得我们可以高效地、端到端地训练神经网络模型,不再依赖早期训练 神经网络时的预训练和逐层训练等比较低效的方法。