算法面试必备-----逻辑回归
算法面试必备-----逻辑回归
- 算法面试必备-----逻辑回归
- 对数几率回归(逻辑回归)
- 问题描述
- 二分类任务
- 单位阶跃函数(unit-step function)
- 对数几率函数(logistics function)---Sigmoid函数
- 图像
- 带入Sigmoid函数推导一下
- 本质
- 优点
- 推导与求解
- 公式推导
- 极大似然估计法
- 用最大似然估计法来求解
- 问题:逻辑回归相比于线性回归,有何异同?
- 多分类学习
- 基本思路
- 经典拆分策略
- “一对一”(One VS One,简称OvO)
- “一对其余”(One VS Rest,简称OvR)
- “多对多”(Many VS Many,简称MvM)
- 类别不平衡问题
- 不同类别样例数的影响
- 类别不平衡class-imbalance
- 处理方法(再缩放rescaling)
- 当正反可能性相同
- 假设训练集是样本总体的无偏采样
- 无法基于训练集类别的数量推断真实几率
- “欠采样”(undersampling)
- EasyEnsemble算法
- “过采样”(oversampling)
- “阈值移动” threshold-moving
- 问题:当使用逻辑回归处理多标签的分类问题时,有哪些常见做法,分别应用于哪些场景,它们之间有怎样的关系?
算法面试必备-----逻辑回归
对数几率回归(逻辑回归)
问题描述
使用回归模型来完成分类任务
只需要找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来
二分类任务
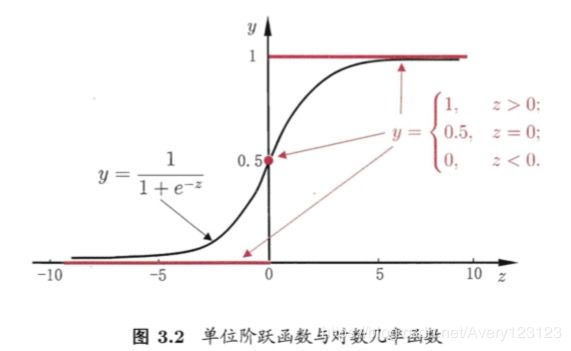
单位阶跃函数(unit-step function)
对数几率函数(logistics function)—Sigmoid函数
图像
带入Sigmoid函数推导一下
本质
用线性回归模型的结果去逼近真是你标记的对数几率
这里的几率是X取1的相对可能性
我们关注的是X与ln(y/1-y)的关系,而不是X与y的关系
优点
推导与求解
公式推导
极大似然估计法
用最大似然估计法来求解
问题:逻辑回归相比于线性回归,有何异同?
分析与解答
多分类学习
基本思路
将多分类分解成多个二分类
经典拆分策略
“一对一”(One VS One,简称OvO)
“一对其余”(One VS Rest,简称OvR)
“多对多”(Many VS Many,简称MvM)
类别不平衡问题
不同类别样例数的影响
类别不平衡class-imbalance
处理方法(再缩放rescaling)
当正反可能性相同
假设训练集是样本总体的无偏采样
无法基于训练集类别的数量推断真实几率
现有技术的三类做法
“欠采样”(undersampling)
直接对训练集中的反类样例进行,即去除一些反样例使得正,反类样例数目接近,再进行学习,这样可能会丢失一些重要的信息
EasyEnsemble算法
将反例划分为若干个集合供不同的学习器使用每个学习器都进行了欠采样
这样全局来看不会丢失重要信息
“过采样”(oversampling)
对训练集中的正类样例进行,即增加一些正例使得正、反例数目接近,然后再进行学习
“阈值移动” threshold-moving
问题:当使用逻辑回归处理多标签的分类问题时,有哪些常见做法,分别应用于哪些场景,它们之间有怎样的关系?
分析与解答
使用哪一种办法来处理多分类的问题取决于具体问题的定义 。
如果一个样本只对应于一个标签,我们可以假设每个样本属于不同标签 的概率服从于几何分布,使用多项式逻辑回归( Softmax Regression ) 来进行分类
当存在样本可能居于多个标签的情况时,我们可以训练 k个二分类的逻辑回归分类器 。第 i 个分类器用以区分每个样本是否可以归为第 i 类,训练该分类器时,需要把标签重新整理为“第 i 类标签 ” 与”非第 i 类标签“两类遇过这样的刃、j去 3 我们就解决了每个样本可能拥有多个标签的情况 。