- CompletableFuture
Momentary_SixthSense
python开发语言后端javamysqlide
CompletableFuture是由Java8引入的,在Java8之前我们一般通过Future实现异步。Future用于表示异步计算的结果,只能通过阻塞或者轮询的方式获取结果,而且不支持设置回调方法,Java8之前若要设置回调一般会使用guava的ListenableFuture,回调的引入又会导致臭名昭著的回调地狱。CompletableFuture对Future进行了扩展,可以通过设置回调的
- Real-World Blur Dataset for Learning and Benchmarking Deblurring Algorithms
钟屿
深度学习
用于学习和评估去模糊算法的真实世界模糊数据集摘要近年来,针对相机抖动和物体运动模糊的单幅图像去模糊提出了许多基于学习的方法。为了将这些方法推广到真实世界的模糊场景,包含大量真实模糊图像及其对应的清晰真实图像(groundtruth)的数据集至关重要。然而,目前尚不存在这样的数据集,因此所有现有方法都依赖于合成数据集,这导致它们无法有效去除真实世界图像的模糊。在本工作中,我们提出了一个用于学习和评估
- 一起学大模型 - LangChain 的 OutputParser
做个天秤座的程序猿
langchainoutPutParser大模型
文章目录前言一、OutputParser的概述二、JSONOutputParser三、自定义格式解析器1.假设的自定义格式2.实现CustomFormatOutputParser3.更复杂的自定义格式四、正则表达式解析器1.示例:正则表达式解析器2.假设的语言模型输出3.实现RegexOutputParser4.更复杂的示例5.说明五、表格解析器1.假设的表格数据2.实现TableOutputPa
- python 协程进阶
cliffordl
asyncpythonpython开发语言
python协程实现python协程进阶python生成器的作用协程在多个模型流式输出中的使用实例文章目录1.协程基础1.1.协程名词解释1.2.基本工作流程1.3.async协程执行1.3.1.协程顺序执行(asyncio.run)1.3.2.协程顺序执行(await)1.3.3.协程同步执行(asyncio.create_task)2.可等待对象(Awaitables)2.1.Coroutin
- 【Lua】题目小练2
大飞pkz
Lualua开发语言游戏开发Lua题目
1.localt={a=1}localmt={__index=function(table,key)returnkey.."_default"end}setmetatable(t,mt)print(t.a)print(t.b)✅1b_default2.观察并说明以下代码会不会报错,如果不会,最后输出什么:MyClass={}MyClass.__index=MyClassfunctionMyClas
- Unity面试——lua(三)
简述Lua有哪8个类型?简述用途?nil空——可以表示无效值,全局变量(默认赋值为nil),赋值nil,使其被删除number整数table表——string字符userdata自定义function函数bool布尔thread线程If语句if(布尔表达式1)then–[在布尔表达式1为true时执行该语句块--]elseif(布尔表达式2)then–[在布尔表达式2为true时执行该语句块--]
- Lua 打印输出完整 table 表
奶酪Cheese
lua开发语言
代码如下:functiondump(o)localt={}local_t={}local_n={}localspace,deep=string.rep('',2),0localtype=_ENV.typelocalfunction_ToString(o,_k)iftype(o)==('number')thentable.insert(t,o)elseiftype(o)==('string')the
- Lua _G表 和 _ENV表
定义在所有函数外部的变量我们可以称之为全局变量(GlobalVariable),它的作用域默认是整个程序。但Lua作为一种嵌入式语言,代码段(chunk)都是由宿主应用调用的,它自身都不知道会被嵌入到哪个应用程序中。为了解决这个问题,它并没有使用全局变量,而是通过table对全局变量进行模拟。我们可以认为Lua语言把所有的全局变量保存在一个称为全局环境(GlobalEnvironment)的普通表
- xLua热更新解决方案知识点汇总
窗外听轩雨
Lua热更新luaunityunity3d
XLua热更新解决方案知识点汇总文章目录XLua热更新解决方案知识点汇总前言热更新的本质C#CallLua相关知识点Lua解析器:LuaEnvC#获取Lua的基础类型C#获取Lua的全局函数functionC#获取Lua的表TableLuaCallC#相关知识点程序主入口Lua调用C#的类Lua调用C#枚举Lua调用C#的数组Lua调用C#的ListLua调用C#的DictionaryLua调用C
- XLua个人学习——C#访问Lua
一枚骰子
学习lua开发语言xLua
目录0.引言1.访问基本数据类型全局变量2.访问全局的table2.1.映射到class或struct2.2.映射到一个interface2.3.映射到List、Dictionary2.4.映射到LuaTable类3.访问全局函数3.1映射到delegate3.2映射到LuaFunction4.官方使用建议0.引言本文是个人学习xLua中C#访问Lua的一些知识点总结。参考教程的是官方教程:xLu
- 80端口被占用,查本地哪个程序占用
静西子
服务器linux运维
netstat-ano|findstr":80"查看pid的路径wmicprocesswhere"ProcessId=4628"getExecutablePath
- stable diffusion-系统课程:0基础系统性学习AI绘画,小白也能轻松上手
顺心网创
本课程是AI绘画工具stablediffusion的系统课程,内容通俗且细致,让小白也能上手。课程大纲基础部分1.前置要求+整合包安装+启动器使用2.纯净原版安装+使用介绍3.文生图精讲4.图生图精讲5.涂鸦、局部重绘、涂鸦重绘6.上传蒙版、批量处理7.模型精讲8.提示词精讲9.插件的认识与安装10.脚本的安装及使用11controlnet基础讲解12.cn-线性控制类型13.cn-深度和法线进阶
- Redis的ziplist与hashtable性能对比测试
无级程序员
java数据库大数据
测试一下ziplist长度为2048时性能。机器为4C,8G虚拟机另外,记录一下,200个节点的Redis集群要消耗大约200mbps带宽用于节点间通讯。
- PGSql性能测试
无级程序员
数据库大数据
一个40亿的表,分成128个区,16384个slot,每个表分区大约3000W数据,每个slot大约25W数据,虚拟机8C16G,1T空间,测试导出一个slot数据性能,结果如下:select*fromtablewhereslot_id=0;以slot_id为索引:大约100多秒,以slot_id和slice_id为索引时大约2秒,很奇怪的结果。另外,数据增加到60亿,即每个表4500W数据时,一
- hive 分区表select全部数据_hive分区表
Xenophon Tony
hive分区表select全部数据
内部表和外部表内部表:createtable,copy数据到warehouse,删除表时数据也会删除外部表:createexternaltable,不copy数据到warehouse,删除表时数据不会删除表的分区分区的好处:如果不建立分区的话,则会全表扫描数据通过目录划分分区,分区字段是特殊字段目录结构:/pub/{dt}/{customer_id}/添加分区:ALTERTABLEfsADDPAT
- MySQL部门员工表实验
2301_81097039
数据库mysql
一、要求(一)数据表1、dept表CREATETABLEdept(deptnoINT(2)NOTNULLCOMMENT'部门编号',dnameVARCHAR(15)COMMENT'部门名称',locVARCHAR(20)COMMENT'地理位置');--添加主键ALTERTABLEdeptADDPRIMARYKEY(deptno);--添加数据INSERTINTOdept(deptno,dname
- Django ORM系统
1.ORM基础概念1.1什么是ORM?ORM(ObjectRelationalMapping,对象关系映射)是一种编程技术,用于在面向对象编程语言中实现不同类型系统的数据转换。在Django中,ORM充当业务逻辑层和数据库层之间的桥梁。核心映射关系:类(Class)↔数据库表(Table)类实例(Instance)↔表记录(Row)类属性(Attribute)↔表字段(Field)1.2ORM的优
- [NIPST AI]对抗性机器学习攻击和缓解的分类和术语
Anooyman
人工智能网络安全人工智能大语言模型网络安全安全
原文link:https://nvlpubs.nist.gov/nistpubs/ai/NIST.AI.100-2e2025.pdfIntroduction人工智能(AI)系统在过去几年中持续全球扩展。这些系统正在被众多国家开发并广泛部署于各自的经济体系中,人们在生活的许多领域都获得了更多使用AI系统的机会。本报告区分了两大类AI系统:预测型AI(PredictiveAI,PredAI)和生成型A
- 跟小朋友学英语25——20220412
李杨手记
群内打卡:1.复习卡片今天晚上复习了近三十张卡片。牛仔好像记得不牢(其实是我有期待)。这两天没有好好听前两周的音频,今晚把音频重新调整一下。如果晚上没有专门的时间听,就睡前再磨一下耳朵。2.复习指定绘本FridaKhalo读了两遍,但都没读完,第二遍还差两页,孩子的注意力就跑到别的书上去了。后来我们阅读了甜心英语的绘本《Rainbowdiningtable》。读完后还一起讨论。最近陪伴精读绘本的能
- C# 代码(`Hashtable` 和 `SortedList`)
张謹礧
c#哈希算法开发语言
一、Hashtable(哈希表)1.基本概念非泛型集合:存储键值对(object类型),通过哈希算法实现快速查找。线程安全:默认非线程安全,可通过Hashtable.Synchronized创建线程安全版本。键的唯一性:键必须唯一,且不可为null(值可为null)。2.创建与初始化//创建空的HashtableHashtablehashtable=newHashtable();//创建并初始化
- 嵌入式硬件篇---单稳态&多谐&施密特电路
Atticus-Orion
嵌入式硬件篇嵌入式知识篇嵌入式硬件单片机
一、单稳态触发器(MonostableMultivibrator)1.电路连线图+Vcc|┌─────┐│R1│└─────┘|┌─────┐TH(6)─────┤││││C1│││││└─────┘│││└───────┐│││┌───────┴───────┐││││DIS(7)TR(2)─────触发信号││││││││┌────┴────┐│││││└────────┤0.01μF││││
- 聊聊flink的RpcService
go4it
序本文主要研究一下flink的RpcServiceRpcServiceflink-release-1.7.2/flink-runtime/src/main/java/org/apache/flink/runtime/rpc/RpcService.javapublicinterfaceRpcService{StringgetAddress();intgetPort();CompletableFutu
- MySQL(141)如何处理重复数据问题?
辞暮尔尔-烟火年年
MySQLmysql数据库
处理重复数据问题是数据管理中的一个常见挑战。重复数据会影响数据库的性能、占用资源,并且可能导致数据分析结果的偏差。以下是处理重复数据问题的详细步骤以及结合代码的示例。一、识别重复数据首先,需要识别数据库中的重复数据。可以使用SQL查询来查找重复的数据。示例:假设我们有一个名为employees的表,其中包含以下字段:id、name和email。CREATETABLEemployees(idINTP
- 2018-09-08 感冒加鼻窦炎了,吃了点药
五大RobertWu伍洋
阿奇霉素分散片怎么吃http://ypk.39.net/882513/manual【药品名称】通用名称:阿奇霉素分散片英文名称:AzithromycinDispersibleTablets【用法用量】以阿奇霉素分散片治疗感染疾病,服用前用水分散后口服直接吞服。其疗程及使用方法如下:成人:1.沙眼衣原体或敏感淋病奈瑟菌所致性传播疾病,仅需单次口服本品1g。2.治疗小儿咽炎、扁桃体炎,一日按体重12m
- 简单英语语法2 - 可数与不可数名词
louyang
1可数名词这些名词代表的东西,可以被一个个数出来。pen,computer,bottle,spoon,desk,cup,television,chair,shoe,finger,flower,camera,stick,balloon,book,table,comb,etc.大多数名词的复数是-直接+spens,computers,bottles,spoons,desks,cups,televisi
- 我在黑马程序员学web前端
新手来了@click
前端
1网页由三部分组成1.、html负责网页的结构2.css、负责网页的美化,控制网页元素的样式3、js,负责网页交互html常见的标签:1、form表单input输入框select下拉菜单option下拉列表2、table表格thead表头tbody是表体tr行th表头加粗td是列br是换行2/CSS常见的三种引入方式行内样式、内部样式、外部样式用link关键字常用的元素选择器:标签选择器、id选择
- 浅谈EXT2文件系统----inode table
巭犇
文件系统linux数据库运维
Inodetable概述在EXT2文件系统中,inode表(InodeTable)是一个非常重要的结构,用于存储文件和目录的元数据。每个文件和目录都由一个inode(索引节点)来表示,inode中包含了关于该文件或目录的关键信息,如文件的大小、权限、所属用户、时间戳以及指向数据块的指针等。EXT2文件系统将所有inode结构集中存储在inode表中。内核源码structext2_inode{__l
- 数据并表技术全面指南:从基础JOIN到分布式数据融合
熊猫钓鱼>_>
分布式
引言在现代数据处理和分析领域,数据并表(TableJoin)技术是连接不同数据源、整合分散信息的核心技术。随着企业数据规模的爆炸式增长和数据源的日益多样化,传统的数据并表方法面临着前所未有的挑战:性能瓶颈、内存限制、数据倾斜、一致性问题等。如何高效、准确地进行大规模数据并表,已成为数据工程师和架构师必须掌握的关键技能。数据并表不仅仅是简单的SQLJOIN操作,它涉及数据建模、算法优化、分布式计算、
- oracle存储过程日志打印,如何在oracle存储过程中逐行打印
昂图
oracle存储过程日志打印
我正在执行一个存储过程,但它在某个时候失败了,当前错误代码不帮我找到错误的位置和确切位置我想知道它正在失败,所以想要在执行时逐行输出。例如:如何在oracle存储过程中逐行打印createorreplace--decaringrequiredvariablePROCEDURE"PROC_DATA_TABLE_DETAILS"ISFORTABLEDETAILSIN(SELECT*FROMuser_t
- Oracle ERP MetaERP采购PO 后台表
anpeng2025
华为MetaERPSAP专题OracleERPoracleOracleERP数据库sap算法
OracleERPMetaERP采购PO后台表TABLE-PO.EDW_PO_VENDOR_HIERARCHIESTABLE-PO.FND_FUNCTION_PARAMETER_MAPTABLE-PO.FND_NOTIFICATIONSTABLE-PO.POA_BIS_SAVINGSTABLE-PO.POA_BIS_SAVINGS_EFCTABLE-PO.POA_BIS_SAVINGS_RPTTA
- sql统计相同项个数并按名次显示
朱辉辉33
javaoracle
现在有如下这样一个表:
A表
ID Name time
------------------------------
0001 aaa 2006-11-18
0002 ccc 2006-11-18
0003 eee 2006-11-18
0004 aaa 2006-11-18
0005 eee 2006-11-18
0004 aaa 2006-11-18
0002 ccc 20
- Android+Jquery Mobile学习系列-目录
白糖_
JQuery Mobile
最近在研究学习基于Android的移动应用开发,准备给家里人做一个应用程序用用。向公司手机移动团队咨询了下,觉得使用Android的WebView上手最快,因为WebView等于是一个内置浏览器,可以基于html页面开发,不用去学习Android自带的七七八八的控件。然后加上Jquery mobile的样式渲染和事件等,就能非常方便的做动态应用了。
从现在起,往后一段时间,我打算
- 如何给线程池命名
daysinsun
线程池
在系统运行后,在线程快照里总是看到线程池的名字为pool-xx,这样导致很不好定位,怎么给线程池一个有意义的名字呢。参照ThreadPoolExecutor类的ThreadFactory,自己实现ThreadFactory接口,重写newThread方法即可。参考代码如下:
public class Named
- IE 中"HTML Parsing Error:Unable to modify the parent container element before the
周凡杨
html解析errorreadyState
错误: IE 中"HTML Parsing Error:Unable to modify the parent container element before the child element is closed"
现象: 同事之间几个IE 测试情况下,有的报这个错,有的不报。经查询资料后,可归纳以下原因。
- java上传
g21121
java
我们在做web项目中通常会遇到上传文件的情况,用struts等框架的会直接用的自带的标签和组件,今天说的是利用servlet来完成上传。
我们这里利用到commons-fileupload组件,相关jar包可以取apache官网下载:http://commons.apache.org/
下面是servlet的代码:
//定义一个磁盘文件工厂
DiskFileItemFactory fact
- SpringMVC配置学习
510888780
springmvc
spring MVC配置详解
现在主流的Web MVC框架除了Struts这个主力 外,其次就是Spring MVC了,因此这也是作为一名程序员需要掌握的主流框架,框架选择多了,应对多变的需求和业务时,可实行的方案自然就多了。不过要想灵活运用Spring MVC来应对大多数的Web开发,就必须要掌握它的配置及原理。
一、Spring MVC环境搭建:(Spring 2.5.6 + Hi
- spring mvc-jfreeChart 柱图(1)
布衣凌宇
jfreechart
第一步:下载jfreeChart包,注意是jfreeChart文件lib目录下的,jcommon-1.0.23.jar和jfreechart-1.0.19.jar两个包即可;
第二步:配置web.xml;
web.xml代码如下
<servlet>
<servlet-name>jfreechart</servlet-nam
- 我的spring学习笔记13-容器扩展点之PropertyPlaceholderConfigurer
aijuans
Spring3
PropertyPlaceholderConfigurer是个bean工厂后置处理器的实现,也就是BeanFactoryPostProcessor接口的一个实现。关于BeanFactoryPostProcessor和BeanPostProcessor类似。我会在其他地方介绍。PropertyPlaceholderConfigurer可以将上下文(配置文件)中的属性值放在另一个单独的标准java P
- java 线程池使用 Runnable&Callable&Future
antlove
javathreadRunnablecallablefuture
1. 创建线程池
ExecutorService executorService = Executors.newCachedThreadPool();
2. 执行一次线程,调用Runnable接口实现
Future<?> future = executorService.submit(new DefaultRunnable());
System.out.prin
- XML语法元素结构的总结
百合不是茶
xml树结构
1.XML介绍1969年 gml (主要目的是要在不同的机器进行通信的数据规范)1985年 sgml standard generralized markup language1993年 html(www网)1998年 xml extensible markup language
- 改变eclipse编码格式
bijian1013
eclipse编码格式
1.改变整个工作空间的编码格式
改变整个工作空间的编码格式,这样以后新建的文件也是新设置的编码格式。
Eclipse->window->preferences->General->workspace-
- javascript中return的设计缺陷
bijian1013
JavaScriptAngularJS
代码1:
<script>
var gisService = (function(window)
{
return
{
name:function ()
{
alert(1);
}
};
})(this);
gisService.name();
&l
- 【持久化框架MyBatis3八】Spring集成MyBatis3
bit1129
Mybatis3
pom.xml配置
Maven的pom中主要包括:
MyBatis
MyBatis-Spring
Spring
MySQL-Connector-Java
Druid
applicationContext.xml配置
<?xml version="1.0" encoding="UTF-8"?>
&
- java web项目启动时自动加载自定义properties文件
bitray
javaWeb监听器相对路径
创建一个类
public class ContextInitListener implements ServletContextListener
使得该类成为一个监听器。用于监听整个容器生命周期的,主要是初始化和销毁的。
类创建后要在web.xml配置文件中增加一个简单的监听器配置,即刚才我们定义的类。
<listener>
<des
- 用nginx区分文件大小做出不同响应
ronin47
昨晚和前21v的同事聊天,说到我离职后一些技术上的更新。其中有个给某大客户(游戏下载类)的特殊需求设计,因为文件大小差距很大——估计是大版本和补丁的区别——又走的是同一个域名,而squid在响应比较大的文件时,尤其是初次下载的时候,性能比较差,所以拆成两组服务器,squid服务于较小的文件,通过pull方式从peer层获取,nginx服务于较大的文件,通过push方式由peer层分发同步。外部发布
- java-67-扑克牌的顺子.从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的.2-10为数字本身,A为1,J为11,Q为12,K为13,而大
bylijinnan
java
package com.ljn.base;
import java.util.Arrays;
import java.util.Random;
public class ContinuousPoker {
/**
* Q67 扑克牌的顺子 从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。
* 2-10为数字本身,A为1,J为1
- 翟鸿燊老师语录
ccii
翟鸿燊
一、国学应用智慧TAT之亮剑精神A
1. 角色就是人格
就像你一回家的时候,你一进屋里面,你已经是儿子,是姑娘啦,给老爸老妈倒怀水吧,你还觉得你是老总呢?还拿派呢?就像今天一样,你们往这儿一坐,你们之间是什么,同学,是朋友。
还有下属最忌讳的就是领导向他询问情况的时候,什么我不知道,我不清楚,该你知道的你凭什么不知道
- [光速与宇宙]进行光速飞行的一些问题
comsci
问题
在人类整体进入宇宙时代,即将开展深空宇宙探索之前,我有几个猜想想告诉大家
仅仅是猜想。。。未经官方证实
1:要在宇宙中进行光速飞行,必须首先获得宇宙中的航行通行证,而这个航行通行证并不是我们平常认为的那种带钢印的证书,是什么呢? 下面我来告诉
- oracle undo解析
cwqcwqmax9
oracle
oracle undo解析2012-09-24 09:02:01 我来说两句 作者:虫师收藏 我要投稿
Undo是干嘛用的? &nb
- java中各种集合的详细介绍
dashuaifu
java集合
一,java中各种集合的关系图 Collection 接口的接口 对象的集合 ├ List 子接口 &n
- 卸载windows服务的方法
dcj3sjt126com
windowsservice
卸载Windows服务的方法
在Windows中,有一类程序称为服务,在操作系统内核加载完成后就开始加载。这里程序往往运行在操作系统的底层,因此资源占用比较大、执行效率比较高,比较有代表性的就是杀毒软件。但是一旦因为特殊原因不能正确卸载这些程序了,其加载在Windows内的服务就不容易删除了。即便是删除注册表中的相 应项目,虽然不启动了,但是系统中仍然存在此项服务,只是没有加载而已。如果安装其他
- Warning: The Copy Bundle Resources build phase contains this target's Info.plist
dcj3sjt126com
iosxcode
http://developer.apple.com/iphone/library/qa/qa2009/qa1649.html
Excerpt:
You are getting this warning because you probably added your Info.plist file to your Copy Bundle
- 2014之C++学习笔记(一)
Etwo
C++EtwoEtwoiterator迭代器
已经有很长一段时间没有写博客了,可能大家已经淡忘了Etwo这个人的存在,这一年多以来,本人从事了AS的相关开发工作,但最近一段时间,AS在天朝的没落,相信有很多码农也都清楚,现在的页游基本上达到饱和,手机上的游戏基本被unity3D与cocos占据,AS基本没有容身之处。so。。。最近我并不打算直接转型
- js跨越获取数据问题记录
haifengwuch
jsonpjsonAjax
js的跨越问题,普通的ajax无法获取服务器返回的值。
第一种解决方案,通过getson,后台配合方式,实现。
Java后台代码:
protected void doPost(HttpServletRequest req, HttpServletResponse resp)
throws ServletException, IOException {
String ca
- 蓝色jQuery导航条
ini
JavaScripthtmljqueryWebhtml5
效果体验:http://keleyi.com/keleyi/phtml/jqtexiao/39.htmHTML文件代码:
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title>jQuery鼠标悬停上下滑动导航条 - 柯乐义<
- linux部署jdk,tomcat,mysql
kerryg
jdktomcatlinuxmysql
1、安装java环境jdk:
一般系统都会默认自带的JDK,但是不太好用,都会卸载了,然后重新安装。
1.1)、卸载:
(rpm -qa :查询已经安装哪些软件包;
rmp -q 软件包:查询指定包是否已
- DOMContentLoaded VS onload VS onreadystatechange
mutongwu
jqueryjs
1. DOMContentLoaded 在页面html、script、style加载完毕即可触发,无需等待所有资源(image/iframe)加载完毕。(IE9+)
2. onload是最早支持的事件,要求所有资源加载完毕触发。
3. onreadystatechange 开始在IE引入,后来其它浏览器也有一定的实现。涉及以下 document , applet, embed, fra
- sql批量插入数据
qifeifei
批量插入
hi,
自己在做工程的时候,遇到批量插入数据的数据修复场景。我的思路是在插入前准备一个临时表,临时表的整理就看当时的选择条件了,临时表就是要插入的数据集,最后再批量插入到数据库中。
WITH tempT AS (
SELECT
item_id AS combo_id,
item_id,
now() AS create_date
FROM
a
- log4j打印日志文件 如何实现相对路径到 项目工程下
thinkfreer
Weblog4j应用服务器日志
最近为了实现统计一个网站的访问量,记录用户的登录信息,以方便站长实时了解自己网站的访问情况,选择了Apache 的log4j,但是在选择相对路径那块 卡主了,X度了好多方法(其实大多都是一样的内用,还一个字都不差的),都没有能解决问题,无奈搞了2天终于解决了,与大家分享一下
需求:
用户登录该网站时,把用户的登录名,ip,时间。统计到一个txt文档里,以方便其他系统调用此txt。项目名
- linux下mysql-5.6.23.tar.gz安装与配置
笑我痴狂
mysqllinuxunix
1.卸载系统默认的mysql
[root@localhost ~]# rpm -qa | grep mysql
mysql-libs-5.1.66-2.el6_3.x86_64
mysql-devel-5.1.66-2.el6_3.x86_64
mysql-5.1.66-2.el6_3.x86_64
[root@localhost ~]# rpm -e mysql-libs-5.1
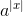 ), not u ⇒ smaller and faster to work with (u mod p fits in one machine word)
), not u ⇒ smaller and faster to work with (u mod p fits in one machine word)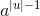 mod p)] mod p = [(u mod p) − ord(c) · (
mod p)] mod p = [(u mod p) − ord(c) · (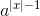 mod p)] mod p
mod p)] mod p