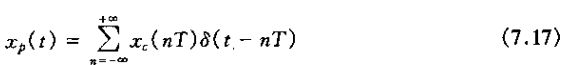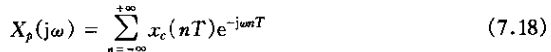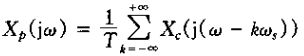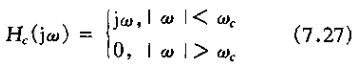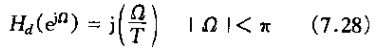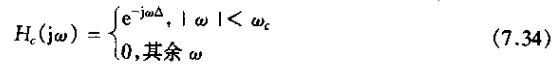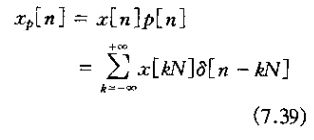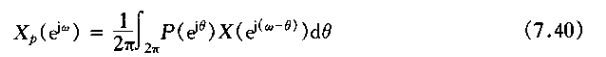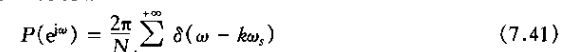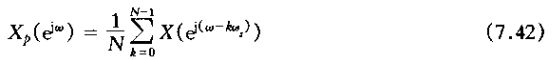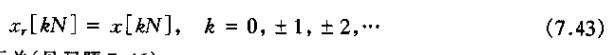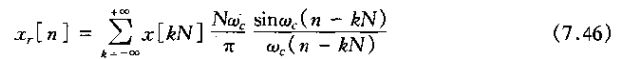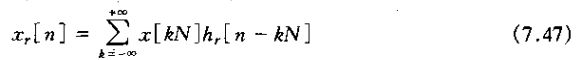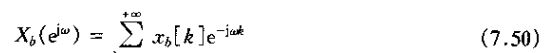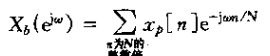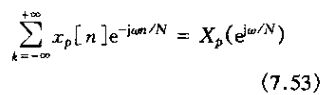《信号与系统学习笔记》—采样(二)
注:本博客是基于奥本海姆《信号与系统》第二版编写,主要是为了自己学习的复习与加深。
一、连续时间信号的离散时间处理
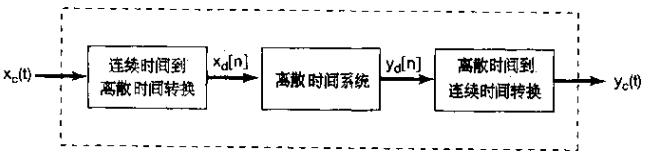
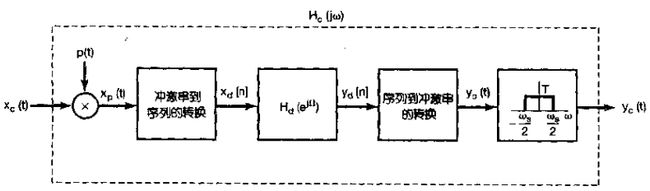
1、在很多应用中,首先把一个连续时间信号转换为一个离散时间信号,然后进行处理,处理完后再把它转换为连续时间信号。广而言之,对连续时间信号的折中处理方法可以看成下图所示的三个环节的级联,其中xc(t)和yc(t)都是连续时间洗你号,而xd(t)和yd(t)都是对应的离散时间信号。
通过一个周期采样的过程(其采样频率满足采样定理中的条件),连续时间洗你号xc(t)就可以完全用一瞬时样本值xc(nT)来表示;也就是说,离散时间序列xd[n]以下式
与xc(t)想联系。将xc(t)变换到xd[n]相应于上图中的第一个系统,称为连续时间到离散时间的转换(C/D),而第三个系统是与上述相反的变换,即离散时间到连续时间的转换(D/C)。D/C实现的事作为它的输入的各样本点之间的内插;也就是说,经D/C后产生一个连续时间信号yc(t),该yc(t)与其输入的离散时间信号yd(t)以下式关联
这一概念在下图中表示更为明显。
为了研究连续时间信号xc(t)和它的离散时间表示xd(t)之间的关系,可以把从连续时间到离散时间的变换表示成一个周期采样的过程,再紧跟着一个把冲激串映射成一个序列环节。这两步都表示在下图中
图中的第一步代表一个采样过程,冲激串xp(t)就是一个冲激序列,各冲激串的幅度与xc(t)的样本值相对应,而在时间间隔上等于采样周期T。然后,在从冲激串到离散时间序列的转换中,得到xd(t);这就是以xc(t)的阉割版之为序列值得同一序列,但是其单位间隔采用新的自变量n。因此,实际上从样本的冲激串到样本的离散时间序列的转换可认为是一个时间归一化过程。
2、从频域的角度来考察变换也是很有意义的。连续时间的频率变量用w表示,将离散时间的频率变量用![]() 表示,以便加以区分。xc(t)和yc(t)的连续时间博里叶变换分别用Xp(jw)和Yc(tjw)表示;而xd[n]和yd[n]的离散时间博里叶变换分别用
表示,以便加以区分。xc(t)和yc(t)的连续时间博里叶变换分别用Xp(jw)和Yc(tjw)表示;而xd[n]和yd[n]的离散时间博里叶变换分别用![]() 和
和![]() 表示。
表示。
利用xc(t)的样本值来表示xp(t)的连续时间博里叶变换Xp(t)。因为
根据![]() 的博里叶变换是
的博里叶变换是![]() ,所以得到
,所以得到
现在考虑xd[n]的离散时间博里叶变换,即
或者,有
将式(7.18)和式(7.20)进行比较可见,![]() 是通过如下关系关联的:
是通过如下关系关联的:
另外
因此得到
3、可以由序列yn[n]产生一个连续时间冲激串yp(t),二连续时间yc(t)的恢复就可以借助下图所示的低通滤波的办法来实现
现在,用下图所示的整个系统
很清楚,如果图中的离散时间系统是一个恒等系统,而且嘉定满足采样定理中的条件,那么整个系统一定是一个恒等系统。
一)、数字微分器
1、现在来考虑一个连续时间带限微风起的离散时间实现。连续时间微分滤波器的频率响应是
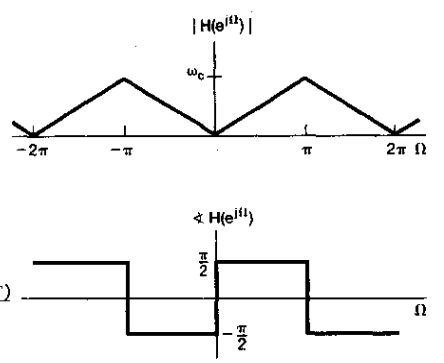
截止频率为wc的带限微风起的频率响应就是
如下图所示
若ws=2wc,则相应的离散时间的频率响应![]() 是
是
如下图所示
利用离散时间频率响应,只要cx(t)的采样中没有混叠产生,yc(t)就一定是xc(t)的导数。
二)、半采样间隔延时
1、为了实现一个连续时间信号的时间移位(延时)问题。于是,根据要求,再输入xc(t)是带限的,且采样率猪狗高一避免混叠的条件下,整个系统的输入、输出是用下列关系联系起来的;
根据时移性质有
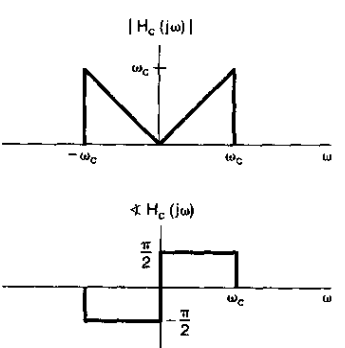
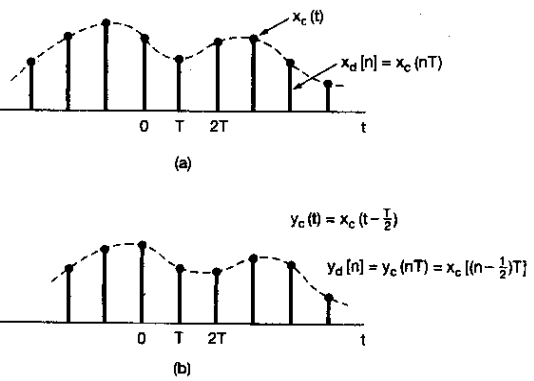
要被其实想爱你的等效连续时间系统必须是带限的,因此选取
也就是说,Hc(jw)对于带限内的信号就相应于式(7.33)的一个时间位移,而对于比wc高的频率则全部滤除。这个频率响应的模和相位特性如下图所示。
对于适当的带限输入来说,若其![]() 如上式所示,就是输入的延时,若△/T是一个整数,序列yd[n]就是xd[n]的延时,即
如上式所示,就是输入的延时,若△/T是一个整数,序列yd[n]就是xd[n]的延时,即
若△/T不为一个整数,式(7.36)就没有任何意义,因为序列仅仅在整数n值上才有定义。然而,我么可以利用带限内插来解释这些情况下的xd[n]和yd[n]之间的关系。洗你号xc(t)和xd[n]是通过采样和带限内插联系在一起的,yc(t)和yd[n]之间也是如此。若![]() r如式(7.35)所示,那么yd[n]就等于序列xd[n]带限内插后移位的样本。如下图所示
r如式(7.35)所示,那么yd[n]就等于序列xd[n]带限内插后移位的样本。如下图所示
这种情况有时候称为半采样间隔延时。
二、离散时间信号采样
一)、脉冲串采样
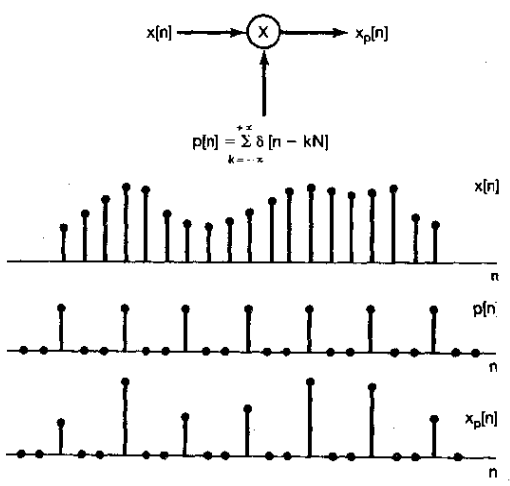
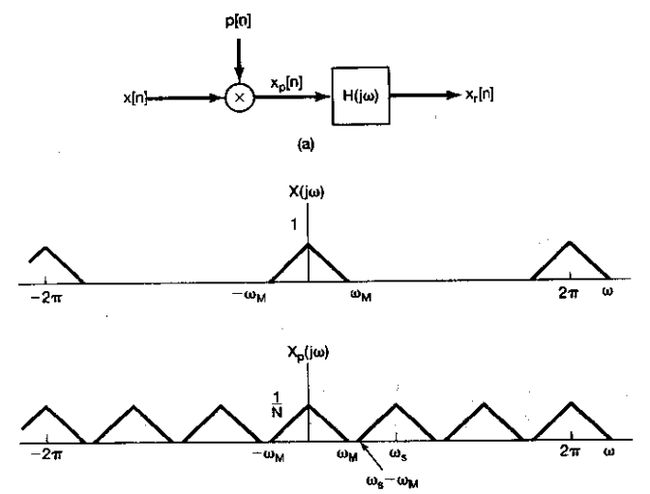
1、与连续时间采样类似,离散时间信号的采样也能表示成下图所示的系统
这里,由采样过程形成的新序列xp[n]在采样周期N的整数倍点上就等于原来的序列x[n],而在采样点之间都是零,即
离散时间采样的频域效果可利用相乘性质得出。于是,由于
在频域内就有
采样序列p[n]的博里叶变换是
式中采样频率ws=2π/N.将式(7.40)和式(7.41)接合起来得
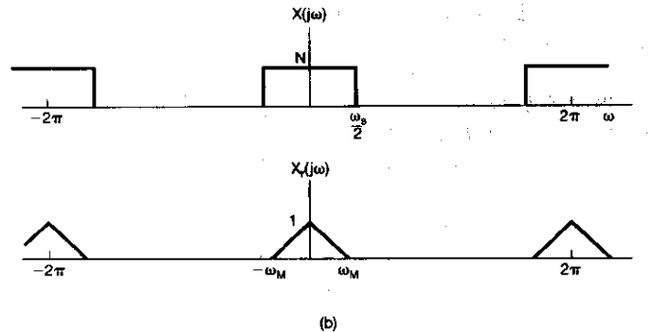
2、利用理想低通滤波器从样本中完全恢复一个离散时间信号
与连续时间采样类似,这两个序列x[n]与xr[n]在采样周期的整数倍点上总是相等的;这就是说
这一点与是否存在混叠无关。
通过对xp[n]利用一个低通滤波器来重建x[n]的过程,也能看成时域的一个内插公式。利用h[n]表示该低通滤波器的单位脉冲响应,则有
重建的序列xr[n]就是
或者等效地写成
上式代表一种理想的带限内插,从而要求实现一个理想低通滤波器。在一般应用中,往往在使用一个适当近似的低通滤波器,这时等效的内插公式就具有如下公式
其中hr[n]就是内插滤波器的单位脉冲响应。与连续时间内插相似,在离散时间内插中,也有零阶保持和一阶保持这样的内插近似。
二)、离散时间抽取与内插
1、离散时间采样的原理在诸如滤波器设计和实现火灾通信中都有许多很多重要应用。对于离散时间采样,往往将该序列用一个新序列xb[n]来代替,而xb[n]就是用xp[n]中的每隔N点上的序列值构成的,即
或者,因为xp[n]和x[n]在N的整数倍上都是相等的,可等效为
![]()
一般就把提取每第N个点上的样本的过程称为抽取。x[n]、xp[n]和xb[n]之间的关系如下图所示
2、为了确定抽取在频域中的效果,希望能求得xb[n]的博里叶变换![]() 之间的关系。为此,注意到
之间的关系。为此,注意到
利用式(7.48),有
如果令n=kN,或者k=n/N,那么就能写成
因为当n不为N的整数倍时,xp[n]=0,所以上式也能写成
进而,式(7.52)的右边就是xp[n]的博里叶变换,即
因此,由式(7.52)和式(7.53)可得
这一关系如下图所示
2、如果这个原始序列x[n]精油连续时间信号采样得到,那么抽取过程就可以看成在连续时间信号上将采样率减少为原来的1/N的结果。因此,为了避免在抽取过程中产生混叠,元序列x[n]的X(ejw)就不能沾满整个频带。换句话说,如果序列能够被丝绸去而又不引入混叠,那么原来的连续时间信号十倍采样过了的,从而元采样率可以减小而不会引发混叠。因此,抽取的过程往往称为间采样。
正如间采样在耨写应用中很有用,叶存在一些情况,需要把一个序列转换到一个较高的等效采样率上,这种称为增采样或内插的过程也是很有用的。增采样基本就是抽取或间减采样的逆过程。