利用经纬度求解两点球面距离(Haversine formula)
利用经纬度求解两点球面距离
Haversine formula
h ( θ ) = s i n 2 ( θ 2 ) = 1 − c o s ( θ ) 2 h(\theta)=sin^2(\frac{\theta}{2})=\frac{1-cos(\theta)}{2} h(θ)=sin2(2θ)=21−cos(θ)
则 h ( θ ) = h ( d R ) = h ( Δ β ) + c o s ( β 1 ) c o s ( β 2 ) h ( Δ α ) h(\theta)=h(\frac{d}{R})=h(\Delta \beta)+cos(\beta_1)cos(\beta_2)h(\Delta \alpha) h(θ)=h(Rd)=h(Δβ)+cos(β1)cos(β2)h(Δα)
- R 表 示 球 面 半 径 , d 表 示 球 面 距 离 , θ 表 示 两 点 与 圆 心 夹 角 弧 度 R表示球面半径,d表示球面距离,\theta表示两点与圆心夹角弧度 R表示球面半径,d表示球面距离,θ表示两点与圆心夹角弧度
- α i 分 别 表 示 两 点 经 度 , β i 表 示 两 点 维 度 , Δ 表 示 差 值 \alpha_i分别表示两点经度,\beta_i表示两点维度,\Delta表示差值 αi分别表示两点经度,βi表示两点维度,Δ表示差值
- 公式全称应该为 h a l f − v e r s i n e half-versine half−versine,即 v e r s i n e : 1 − c o s ( θ ) 的 一 半 versine: 1-cos(\theta)的一半 versine:1−cos(θ)的一半
- 计算时可进一步化解: c o s ( θ ) = s i n ( β 1 ) s i n ( β 2 ) + c o s ( β 1 ) c o s ( β 2 ) c o s ( Δ α ) cos(\theta)=sin(\beta_1)sin(\beta_2)+cos(\beta_1)cos(\beta_2)cos(\Delta \alpha) cos(θ)=sin(β1)sin(β2)+cos(β1)cos(β2)cos(Δα)
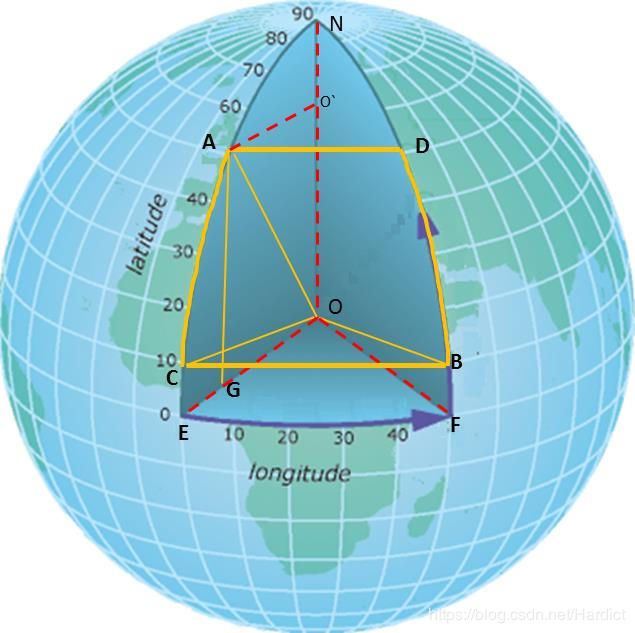
这里求 A B ⌢ \overset{\frown}{AB} AB⌢,显然求得 ∣ A B ∣ |AB| ∣AB∣即可
以 O E F OEF OEF为例, ∠ O E F = Δ α , ∣ E F ∣ = 2 s i n ( Δ α 2 ) \angle OEF=\Delta \alpha,|EF|=2sin(\frac{\Delta \alpha}{2}) ∠OEF=Δα,∣EF∣=2sin(2Δα)R,同理利用维度 ∣ A C ∣ = 2 s i n ( Δ β 2 ) R |AC|=2sin(\frac{\Delta \beta}{2})R ∣AC∣=2sin(2Δβ)R
而对于 ∣ B C ∣ , ∣ A D ∣ |BC|,|AD| ∣BC∣,∣AD∣作 A G ⊥ O E , B H ⊥ O E AG\perp OE,BH \perp OE AG⊥OE,BH⊥OE可得: ∣ A D ∣ = 2 s i n ( Δ α 2 ) ( ∣ O E ∣ c o s ( ∠ A O G ) ) = 2 s i n ( Δ α 2 ) R c o s ( β 1 ) |AD|=2sin(\frac{\Delta \alpha}{2})(|OE|cos(\angle AOG))=2sin(\frac{\Delta \alpha}{2})Rcos(\beta_1) ∣AD∣=2sin(2Δα)(∣OE∣cos(∠AOG))=2sin(2Δα)Rcos(β1)
而四边形 A C B D ACBD ACBD为等腰梯形形
C H = B C − A D 2 , A B 2 = B H 2 + A H 2 = ( B C − C H ) 2 + A C 2 − C H 2 = A C 2 + B C ∗ A D CH=\frac{BC-AD}{2},AB^2=BH^2+AH^2=(BC-CH)^2+AC^2-CH^2=AC^2+BC*AD CH=2BC−AD,AB2=BH2+AH2=(BC−CH)2+AC2−CH2=AC2+BC∗AD
∣ A B ∣ 2 = 4 s i n 2 ( Δ β 2 ) R 2 + 4 s i n 2 ( Δ α 2 ) c o s ( β 1 ) c o s ( β 2 ) R 2 |AB|^2=4sin^2(\frac{\Delta \beta}{2})R^2+4sin^2(\frac{\Delta \alpha}{2})cos(\beta_1)cos(\beta_2)R^2 ∣AB∣2=4sin2(2Δβ)R2+4sin2(2Δα)cos(β1)cos(β2)R2
而要求解的 θ = ∠ A O B , ∣ A B ∣ 2 = 4 s i n 2 ( θ 2 ) R 2 \theta=\angle AOB,|AB|^2=4sin^2(\frac{\theta}{2})R^2 θ=∠AOB,∣AB∣2=4sin2(2θ)R2
得到目标公式 h ( θ ) = h ( Δ β ) + c o s ( β 1 ) c o s ( β 2 ) h ( Δ α ) , A B ⌢ = d = R θ h(\theta)=h(\Delta \beta)+cos(\beta_1)cos(\beta_2)h(\Delta \alpha),\overset{\frown}{AB}=d=R\theta h(θ)=h(Δβ)+cos(β1)cos(β2)h(Δα),AB⌢=d=Rθ
进一步化解 1 − c o s ( θ ) = 1 − c o s ( Δ β ) + c o s ( β 1 ) c o s ( β 2 ) ( 1 − c o s ( Δ α ) ) 1-cos(\theta)=1-cos(\Delta\beta) +cos(\beta_1)cos(\beta_2)(1-cos(\Delta \alpha)) 1−cos(θ)=1−cos(Δβ)+cos(β1)cos(β2)(1−cos(Δα))
c o s ( Δ β ) = c o s ( β 1 ) c o s ( β 2 ) + s i n ( β 1 ) s i n ( β 2 ) cos(\Delta \beta)=cos(\beta_1)cos(\beta_2)+sin(\beta_1)sin(\beta_2) cos(Δβ)=cos(β1)cos(β2)+sin(β1)sin(β2)
可得 c o s ( θ ) = s i n ( β 1 ) s i n ( β 2 ) + c o s ( β 1 ) c o s ( β 2 ) c o s ( Δ α ) cos(\theta)=sin(\beta_1)sin(\beta_2)+cos(\beta_1)cos(\beta_2)cos(\Delta \alpha) cos(θ)=sin(β1)sin(β2)+cos(β1)cos(β2)cos(Δα)