1.图的连通性与连通分量
无向图中若任意两个顶点都是可达的，则图是连通的
有向图中若任意两个顶点都可以到达，则图是强连通的
图的连通分量是顶点在“从......可达”关系下的等价类。即可以理解为其一个子图，所有的连通分量构成图的一个划分。
对于判断无向图连通性，直接用并查集(Union-and-FindSet)维护或者利用bfs、dfs即可
而有向图的连通性，根据起点选择不同结果不同，在起点处bfs、dfs即可判断连通性
2.强连通分量SCC
问题：将有向图分解为强连通分量
Korasaju算法
Korasaju算法利用了图
在拓扑排序后连通分量之间的关系
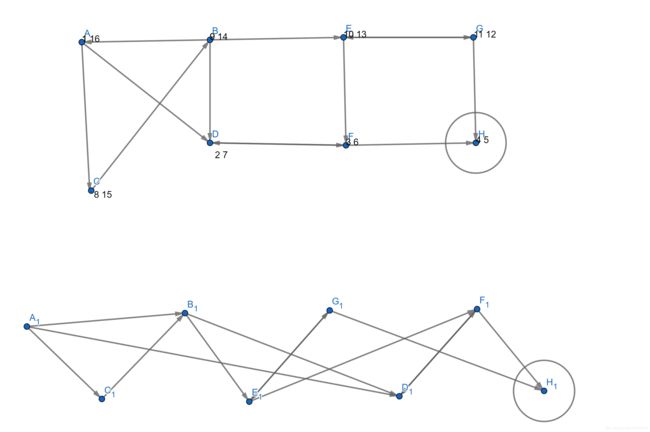
上图有{A,B,C}、{D,F}、{E,G}、{H}四个强连通分量，编号为1,2,3,4
可以看到在下方的拓扑排序中强连通分量被排为了1-->3-->2-->4
引理1：设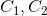
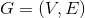为有向图的两个不同强连通分量，若
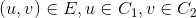，那么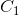
最后完成搜索。换句话说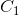在拓扑排序中一定有一个点在
左侧。
那么在转置图中由于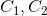为不同强连通分量且有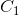到的一条边，那么转置图中一定没有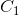到的一条边，从而可以推证算法的准确性。
如果按照{H}-->{D,F}-->{E,G}-->{A,B,C}的顺序访问此图(即转置图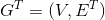
)，即可以按次序分别标记4个强连通分量
算法流程：先将原图拓扑排序，从左向右访问转置图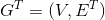，每次访问得到一个连通块即为一个新的强连通分量
缩点：如果以每个强连通分量访问时已统计的强连通分量的数量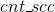
作为其强连通分量的编号，那么图可以化解为一个DAG图，DAG图中每条边可以在访问时直接加入
复杂度分析：空间上该算法需要基础存边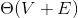
，额外转置图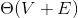，拓扑排序的栈
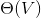，总空间为。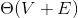
时间上拓扑排序一次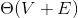，搜索转置图一次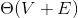，总时间复杂度为。
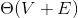#include
#include
#include
#include
#include
Tarjan算法
