《数据结构与算法》——KMP算法(个人理解)
KMP算法
本文将从7个方面对KMP算法以个人理解进行描述,参考书目:严蔚敏教授的《数据结构(C语言版)》
目录
KMP算法
1.什么是KMP算法?
2.经典字符串匹配算法。(老法子,效率低)
3.如何实现next数组?
4.Next数组是完美的标记数组吗?
5.KMP算法过程讲解
6.实现算法
7.对与经典算法比较
1.什么是KMP算法?
KMP算法是为了解决字符串匹配效率问题的优化算法。(非定义)
2.经典字符串匹配算法。(老法子,效率低)
给出两个字符串S母串、T子串以及正整数pos,要求从S母串中第pos位置开始进行匹配直到找到一个与T子串相同的字符串为止,并返回该字符串开始的位置。(注:在本算法中所有的下标均从0开始。 #重新定义数据结构SString,课本上用的是SString,字符串下标从1开始,0下标表示的是字符串的长度。此处直接使用已有数据类型string,并用s.length()表示字符串长度)
算法实现如下:
#include
#include
using namespace std;
int init(string S, string T, int pos){
if (S.length() < T.length() || pos > S.length())
return 0;
int i = pos - 1 , j = 0 ;
while(i < S.length() && j < T.length() ){
cout<= 1
string S,T;
int pos = 1;
//S= "ababcabcacbab" T="abcac"
cin>>S>>T>>pos;
cout< 此种算法的原理是:各位一一比较,相同则比较下一位,不同则进行回退,子串重新从第1位开始,母串则后推一位。此种算法最快需要比较n次(子串的长度),最慢则需比较m*n次,举例说明(1、“asdasdadad”和“asd” 2、字符串“00000000001”和字符串“0001”)
由例2我们不难看出,我们第一次比较完后发现s串的第4位及以前均为0,而T串的前三位也为0,所以第二次比较的时候,无需将子串的第1位和母串的第2位进行比较,则只需从子串的第3位和母串的第4位进行比较即可,即只需子串指针进行回溯,但如何实现这个功能呢?或者说,如何省去中间的比较过程呢?在此我们希望有一个数组可以记录,出现不匹配时对字串进行回溯的位置。这是我们引入一个数组next。
3.如何实现next数组?
这一问题属于KMP算法中的一大难点,它有两种计算方法,一种是针对考试过程中笔算,第二种则是针对机试中的编程问题。
第一种计算方法,这种方法是从网上的一个视频中学到的,用起来是莫名的舒爽。
(原视频找了好久没找到,来自哔哩哔哩的一段5~6分钟的英文讲解视频)用下面的方法也一样,用熟了自然就快了。
第二种方法则是根据原理一步一步理解实现的。
1.先写出子串T,“abcdabcacd”;
2.对其进行标记下标,与参考资料不同,在此字符串是以0为下表开始的,如下表:
| 下标 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 字符 |
a |
b |
c |
d |
A |
b |
c |
a |
c |
d |
| Next |
|
|
|
|
|
|
|
|
|
|
现在的任务即是将表格的第三行进行填充,我们本着的原则就是,能少往前翻就少往前翻。
第一个字符“a”,若是第一个字符就不相同,那么后面的肯定不考虑,所以讲母串向后移一位(在此所有母串的操作暂且不用理会),下一次还是从第一位开始比,所以此处填0,但考虑到和母串一起变化且方便操作,此处改为-1;
第二个字符若不同,则比较前面的字符串,前面的字符串为“a”,没有前后缀之说,所以此处也应填0;
第三个字符若不同,前面的字符串为“ab”,前后缀不同,所以此处返回0;
第四个字符同理,第五个字符若不同,比较字符串“abcd”,所以此处为0;
第六个字符若不同,比较字符串“abcda”,前后子串“a”相同,则下一次比较无需比较第一位,直接从第二个字符开始比较,即返回1;
第七个字符若不同,比较字符串“abcdab”,前后子串“ab”相同,则下次比较可直接从第三个字符开始比较,即返回2;
第八九十个字符位同理。-1 0 0 0 0 1 2 3 1 0
用图和公式表示就是,
算法实现见后文。(字丑勿笑,“前后缀”一名词不知合适否。)
4.Next数组是完美的标记数组吗?
答案显然不是。若如例3所提:字符串“00010001001010000001”和字符串“0000001”进行比较。
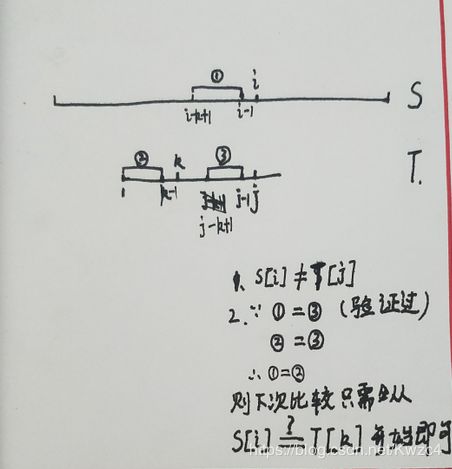
(从1开始记位)当i=4,j=4时,我们不难发现出现了不匹配的情况,若按照上问题到的next数组进行比较的话,则还需要进行 (i,j) = (4,3)、(4,2)、(4,1)的比较,而从字符串上我们能够很清楚的看到j=1、2、3、4时,子串上的字符是完全一样的,所以这些比较就没有必要进行,应该直接从(i,j) = (5,1)进行比较,即让子串中的指针进行了next[next[…..]]的跳跃,如何能够实现这个效果呢?这里引入一个新的数组名称为nextval。
这个数组的获得与上个数组的获得有何不同呢?他们之间的差别其实非常小,仅需在其中加一个判断语句,判断T[j]和T[k]是否相等,如果相等则当前nextval的值与k位上的nextval值相等,否则则和next数组获取值的方式相同。
5.KMP算法过程讲解
KMP算法和的执行过程与普通的字符串查找算法大体无异,而仅有的差别就是,当遇到子母串字符不相匹配时,原算法是子母串指针均进行回溯,而KMP算法则是,子串指针根据next数组进行回溯,母串指针位置不变。即理解KMP算法的前提得将经典的算法过程进行熟悉掌握。
6.实现算法
/*编译环境:
win10专业版
DEV C++ 5.11
TDM-GCC 4.9.2 64bit
*/
#include
#include
using namespace std;
int init(string S, string T, int pos);
int get_Next(string T,int next[]);
int get_Nextval(string T,int nextval[]);
int KMP(string S, string T, int pos);
int main(){
//主函数pos按照字符串的位置进行输入,pos >= 1
string S,T;
int pos = 1;
//S= "ababcabcacbab" T="abcac"
cin>>S>>T>>pos;
cout< S.length())
return 0;
int i = pos - 1 , j = 0 ;
while(i < S.length() && j < T.length() ){
cout<S.length())
return 0 ;
int next[T.length()];
//get_Next(T,next);//求next
get_Nextval(T,next); //求nextval
int i = pos-1,j= 0;
while(i 7.对与经典算法比较
因为子串的长度远比母串小,所以对子串求next数组消耗的时间来换取来回重复回溯母串字符指针的时间这一操作来讲,我们认为是很划算的,因此说KMP算法的效率比较高。但是一般情况下,经典算法的耗时基本趋向o(n+m),所以到现在为止经典算法还没有被完全替代,但对于文件扫描等大型的比较操作来讲,KMP算法的优势就会很明显。
修改记录:
2019-7-7:
KMP函数中while循环中的判断条件添加了强制转换。因为 字符串的 .length()方法返回的是 unsigned long long (int)类型和int型数据比较一直出错 (课本上算法中,第一个字符下标从1开始,不会出现这种比较出错得情况 )