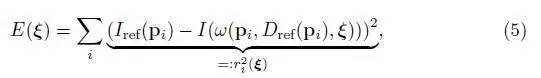【泡泡机器人翻译专栏】LSD-SLAM : 基于直接法的大范围单目即时定位和地图构建方法

转载至https://www.sohu.com/a/166136329_715754

泡泡机器人翻译作品

原文标题：LSD-SLAM: Large-Scale Direct Monocular SLAM

作者：Engel J, Schöps T, Cremers D

翻译：董添

审核：赵博欣 杨雨生

编辑：赵江龙

欢迎个人转发朋友圈；其他机构或自媒体如需转载，后台留言申请授权

摘要

我们提出一种基于直接法的单目SLAM算法，该方法与目前现有直接法相比，能够构建大尺度的，全局一致性的环境地图。我们的方法除了能够基于直接图像配准得到高 度准确的姿态估计外，还能够将三维环境地图实时重构为关键帧的姿态图和对应的半稠密的深度图。这些都是通过对大量像素点对之间的基线立体配准结果滤波后得到的。算法提出了计算尺度漂移的公式，即便是当图像序列的场景尺度变化较大时也能够适用。

LSD-SLAM主要有两个创新点：

(1) 一种新颖的基于（相似变换空间对应的李代数）sim(3)上的直接跟踪法，从而能够很明确的检测到尺度漂移，

(2) 使用一种概率方法，对图像跟踪过程中，处理噪声对深度图像信息的影响。

最终结果证明直接单目SLAM算法能够在CPU上实时运行。

一. 简介

当下，实时单目即时同步定位和地图构建系统（SLAM）和三维空间环境重构俨然成为学术界 流行的研究课题。这里主要有两个原因：(1) 这些技术广泛使用在机器人领域，特别是用于无人飞行器[10, 8, 1]的自主导航中， (2) 还有，增强和虚拟现实技术的应用正逐渐进入大众市场。单目SLAM的主要优点之一，同时也是它的一个最大挑战之一，就是它固有的尺度歧义尺度不确定性这个问题。场景的尺度，不能被观测到，并且随着时间会产生漂移，这也是单目SLAM造成估计误差的主要原因之一。

当然尺度不确定性的优点在于，可以对不同规模大小的空间环境之间走游切换，起到无缝连接的作用，比如从室内桌面上的环境和大规模的户外场景。另一方面，诸如深度或立体视觉相机，这些具备深度信息的传感器，它们所提供的可靠深度信息范围，是有限制的，故而不能像单目相机那样具有尺度灵活性的特点。

1.1相关研究成果.

1.特征点法

基于特征的SLAM方法（包括滤波SLAM[15,19]和关键帧SLAM[15]）的基本思 想是将整个问题——从图像序列中估计几何信息——拆分成两步：首先，从图像中提取一组特征观测量，然后以这些特征变量建立位姿估计函数，计算摄像头的位置信息和构建场景地 图。虽然这种解耦方法简化了整个问题，但是这种方法 存在一个比较大的局限性：仅仅提取使用了图像上符合特征类型的信息，尤其是当使用特征点进行构图与定位时，图像中所包含的直线或曲线边缘信息——大量存在于当前的人工建筑环境中——则不会被考虑。

之前已经有不少文章，提出了获取更多图像信息的方法，包括基于图像边缘特征提取 [16, 6]，甚至是基于图像区域特征提取[5]。然而，高维度空间的特征计算代价比较大，所以这些方法很少在实际中使用。为了重构稠密的环境地图，可以通过多视角立体几何理论，利用已经估计得到摄像头姿态来重构后续的稠密地图[2]。

2.直接法

直接法视觉里程计（VO）是直接利用图像像素点的灰度信息来构图与定位，克 服了特征点提取方法的局限性，可以使用图像上的所有信息。该方法在特征点稀少的环境下仍能达到很高的定位精度与鲁棒性，而且提供了 更多的环境几何信息，这在机器人和增强现实额应用中都是非常有意义的。

直接配准法理论和应用早已经在RGB-D或双目视觉传感器上建立和应用[14, 4]，但是，基于单目相机，使用直接法，来计算视觉里程计的算 法，是近些年才被提出来的：在[24, 20, 21]中的论文中，提出使用泛函变分公式来计算高精度，完全式稠密型深度地图，但是这些方法的计算量比较大并且实时运算时需要GPU。在[9]论文中，提出了一种半稠密型深度滤波器公式，它能够 大大降低计算复杂度，并且可以实时运行在单个CPU上，甚至还可以跑在智能手机上[22]。论文[10]提出直接跟踪法融合特征值提取法（的思想），该算法可以维持很高的图像帧率，甚 至可以跑在嵌入式系统，也可以保持较高的图像帧率。所有这些方法的不足是实质上是计算视觉里程计，它们仅仅 只是在局部范围内跟踪相机运动（和轨迹），并没有考虑创建一个全局，高度一致性 的场景地图，包括对闭环的处理等。

3.位姿图优化

图优化方式是SLAM解决全局地图一致性的一个重要手段，全局地图由一连串相机关键帧组成，这些相机关键 帧组成了姿态图的节点，并且由帧间的位姿关系作为约束条件相连接，这样一个非线性图状结构，可以通过像g2o [18] 那样的通用图优化框架来优化求解。

在文献[14]中，提出了一种基于姿态图的RGB-D SLAM方法，该方法也用到3D点云的几何误差项，可 以在环境纹理稀少的场景中进行图像跟踪。为了处理单目SLAM引起的尺度漂移这个问题，论文[23]提出了基于关键帧的单目SLAM系 统，（其主要思想就是）把相机位姿表示为3D相似变换而不是用刚体运动来计算。

Fig. 1: LSD-SLAM，大尺度单目直接SLAM方 法。 通过对图像光度直接配准和使用概率模型来表示半稠密深度图，生成具有全局一致性的地图。顶部示图：手持式单目相机运动中等距离的过程中实时生成的轨迹图及所有关键帧对 应的点云地图。底部示图：相机轨迹中，部分关键帧图像以及对应的着色半稠 密逆深度图示意。

Fig.2：LSD-SLAM 除了能够重构精准的半稠密三维空间地图，它也能够估计相应深度值的不确定性。示图从左到右的顺序：由于深度值的不确定性，我们使深度服从高斯分布模型，选用不同的深度极大方差， 会呈现出不同效果的点云地图。注意到，，越显稠密的点云地图，往往夹杂着更多的深度不确定性的，未能收敛的噪点。

1.2论文贡献和提纲

我们提出了一种基于直接法的大尺度单目 SLAM算法，该方法不仅仅可以在局地区域内，对相机运动进行跟踪，而且还可以构建全局一致性的大尺度的场景地图。算法使用基于滤波的图像配准方法来估计半稠密深度图。早在论文[9]中，就已经提出过这样的算法方案。全局地图表示成一个姿态图，这个姿态图的节点由相机关键帧组成，姿态图的边由3D相似变换构成，这个模型较好的结合了不断变化的场景尺度，可以检测并纠正累计误差。算法可以实时运行在单个CPU上，可以运行在智 能手机上，充当视觉里程计。这篇论文的主要贡献如下：

(1) 提出了一个基于直接法的大尺度单目 SLAM系 统框架，特别是用了一种新颖的具备环境尺度感知的图像配准算法，来直接估计，关键帧之间的相似变换即：

ξ ∈ sim(3)。

(2)在图像跟踪过程中，通过概率的方法，能够对深度的不确定性进行估计。

二. 预备知识

在本章中，我们会简明扼要的给出相关的数学定义和符号表示。尤其在（2.1小节），我们会总结一下，三维空间位姿如何用李代数的 方式表达。然后（2.2小节）推导出图像直接配准法的实质，即：李群—流形上的 加权最小二乘的最小化优化问题。并在（2.3小节）扼要说明不确定性（协方差矩阵或叫信息矩阵）是如何传播的。

数学符号定义：

矩阵用粗体，大写字母表示，（比如：R）；

向量用粗体，小写字母表示（比如：ξ）；

矩阵的第n行用[⋅]n来表示；

图像用I表示（I : Ω → R）；

逆深度图D : Ω → R+ ；

逆深度方差 V : Ω → R+，其中： Ω⊂ R2 ， Ω 是归一化的像素（二维）坐标点集合，即包含相机内参。

在整篇论文中，三维空间中某一点的深度表示为 z , 它的逆深度用 d 表示，两者的关系即：d = z−1 。

2.1三维空间刚体变换和相似变

三维空间刚体变换

三维空间的刚体变换G ∈ SE(3) ，定义了3D空间位姿的旋转和平移的转换关系，即公式（1）

在优化过程中，相机位姿需要用到刚体变换 SE(3) 李群对应的李 代数 se(3) 计算。 SE(3) 和 se(3) 的转换关系如下：使用指数映射关系（exponential map） G = expse(3)(ξ) ,就可以把六维向量 ξ 从李代数 se(3) 映射到刚体变换李群 SE(3) 上（从而获得刚体变换矩阵G ），反之，使用对数映射关系 ξ = logSE(3)(G) ，就可以把 SE(3) 上的刚体变换矩阵 G 映 射成在李代数 se(3) 上的六维向量 ξ。这里我们约定使用 se(3) 的六维向量 ξ，前三个数表示平移，后三个数表示旋转,来表示位姿，即： ξ ∈ R6 。一个（图像）点从图像帧 i 到图像帧 j 的变换，被记作： ξji 。为了方便起见，我们在se(3)上定义一个乘法 ∘ : se(3) × se(3) → se(3) ，见公式（2）。

此外，我们还定义一个三维投影函数 ω，即：把图像 上的某一点 p 和这点的逆深度值 d ，投影到由ξ 转换的相机 坐标系下，公式（3）。

三维空间相似变换

三维空间的相似变换（ 4 × 4 ）矩阵S ∈ Sim(3) （相似变换空间）定义了旋转，尺度和平移的转换关系，即公式（4）。

如同上述三维空间刚体变换，相似变换空间用对应的李代数 ξ ∈ sim(3) 表示，还要在向量 ξ里额外加上一个自由度，记作： ξ ∈ R7 （七维向量， 三个数表示旋转，三个数表示平移，一个数表示尺度因子）。Sim(3) 和 sim(3) 之间的转换关系（即：指数映射和对数映射），乘法（concatenation operator） ∘ : sim(3) × sim(3) → sim(3)和投影函数 ωs ，与上述 se(3) 的数学表达式相似，更多详情，请参考文献[23]。

2.2 李群流体流形上的加权高斯-牛顿优化方法

两幅图像之间的配准，见公式（5）

可以认为是高斯—牛顿的优化问题，其目的就是要最小化（整个）光度测量误差项二次型（之和），假设图像上的（单个）光度测量误差项，是独立同分布（i.i.d.）的高斯分布残差，那么这个优化问题得到的结果，就是 ξ 的极大似然值。

见公式（7），使用一个左乘复合迭代函数：从初始估计（相机姿态变换）ξ(0) 开始，（高斯-牛顿）每次迭代过程中，左乘更新量 δξ(n) ，这个更新量是通过（误差函数） E 的高斯-牛顿二阶近似求解的最小值得到 的：

其中： J 是残差向量 r = (r1 , ..., rn)T 的求导， 用雅克比矩阵（ JT J ）的方式，去近似（误差函数）E 的二阶海森矩阵，这样求得左乘更新量 δξ(n) ，见公式（6）。

通过不断左乘更新量 δξ(n) ，就得到了更新的（相机姿态）估计，见公式（7），

图像配准过程中会经常发生，相机视野遮挡或光线反射等问题，造成图像配准容易产生外点。为了让配准算法更加鲁棒，论文[14]提出了一种对测 量误差项加权方法，其实质就是加权迭代最小二乘问题。每次迭代过程中去算一个权重矩阵 W = W(ξ (n)) ，它的作用就是（对方差）较大的残差，降 低其权重。

这样，误差函数 E 见公式（8）

于是，它的更新量 δξ(n) 计算就改写成，见公式（9）：

假设残差是独立的随机变量，那么求解相机姿态 ξ(n) 数学模型，就可以看做是公式（10）：

其中左乘误差项（即二阶的海森—逆矩阵），服从高斯分布 N (0, Σξ ) ，二阶海森—逆矩阵的求解就是每次通过前一次迭代 (JT WJ)−1 （用一阶雅克比来近似）计算得到。

实际情况中，残差之间（光度测量误差之间）是高度相关性的， （因为我们假设残差之间是独立不相干的变量i.i.d.，）使得这个协方差 Σξ 仅仅是个下限（这个补充还需要确认）—但是 它仍然包含了噪声之间在不同自由度上的相关性，这一有用信息。注意到，我们这里使用左乘法则，如果使用右乘法则，也可以获得相等的结果。然而，估计协方差 Σξ 取决于乘法的顺序—因此当使用姿态图优化框架的时候，这一 点要考虑进去。这里使用的左乘规则和论文[23]是一致的，然而像g2o [18] 姿态图优化框架，默认的 实现类型是使用右乘规则。

2.3随机变量不确定性的传递

广义上讲不确定性的传递是概率统计学上的方法， X 是随机变量，（具有不确 定性），推导ft X在函数 f (X) 上不确定性。假设随机变量 X 服从高斯分布，且 X 的协方差是 ΣX ，那么 f (X) 的协方差就可以近似表示，见公式（11）。

三. 基于直接法的大范围单目SLAM

我们在3.1小节首先给出整个LSD-SLAM算法的概述，然后在3.2小节，我们简单介绍LSD- SLAM是如何表示地图的。图像跟踪流程详见3.3小节， 深度图估计详见3.4小节，地图优化详见3.4，3.5和3.6小节

图3、算法主要组成部分，分别为图像跟踪、深度图估计和地图优化

3.1算法流程综述

算法有三个主要组成部分，分别为图像跟踪、深度图估计和地图优化。如图3所示。

• 图像跟踪： 连续跟踪从相机获取到的新“图像帧”。也就是说用前一帧图像帧作为初始姿态，估算出当前 参考关键帧和新图像帧之间的刚体变 换 ξ ∈ se(3)

• 深度图估计： 使用被跟踪的“图像帧”，要么对当前关键帧深度更新，要么替换当前关键帧。深度更新是基于像素小基线立体配准的滤波方式，同时耦合对深度地图的正则化，该方法最初在论文[9]中提及。 如果相机移动足够远，就初始化新的关键帧，并把现存相近的关键帧图像点投影到新建立的关键帧上。

• 地图优化模块：一旦关键帧被当前的图像替代-它的深度信息将不会再被进一步 优化-而是通过地图优化模块插入到全局地图中。为了检测闭环和尺度漂移，采用尺度感知的 直接图像配准方法来估计当前帧与现有邻近关键帧之间的相似性变换。

初始化

启动LSD-SLAM系统时，只需要初始化首帧关键帧即可，而关键帧深度信息初步设定为一个方差很大的随机变量。在算法运行最开始的几秒钟，一旦摄像头运动了足够的平移量，LSD-SLAM算 法就会“锁定”到某个特定的深度配置，经过几个关键帧的传递之后，就会收敛到正确的深度配 置。LSD-SLAM初始化方式的进一步评估，超出了本篇论文的范围，将在未来的工作中详细探讨。

3.2地图的数学模型

地图用关键帧的姿态图表示，每个关键帧包括：相机图像，逆深度图，及逆深度方差。相机图像 Ii : Ωi → R，逆深度图 Di : ΩD → R+ ，逆深度方差 Vi : ΩDi → R 。值得注意的是，深度图和方差仅针对像素子集 ΩDi ⊂ Ωi （即：像素图像上的兴趣点集合）, 也就是说，这个子集包含图像上强度梯度比较大的区域，这样就是所说的半稠密地图。关键帧之间的边包含了对应图像之间的相似性变换，以及对应的协方差矩 阵。

3.3 对新图像帧的跟踪：直接图像配准

以当前关键帧作为参考帧，通过最小化方差归一化光度误差来计算当前帧图像相 对参考帧的三维姿态变换。（见如下公式12,13,14）

其中， ∥ ⋅ ∥δ 是Huber范数，（见公式15），应用于归一化的残差上。

通过计算协方差传递公式得到残差方差 σ2 ，原理简述在2.3小节，这里使用了逆深度方差。此外，我们假设图像灰度噪声服从高斯分布。通过迭代重加权高斯-牛顿优化方法使目标函数最小化，请参考2.2小节。

和之前直接法不同的是，我们将深度噪声引入到了最小化光度误差的公式中。对于直接 法的单目SLAM系统来说，不同像素的深度噪声是不同的，完全取决于这个像素被 观测到多少次。—它与RGB-D数据的工作方式不同，即：后者逆深度的不确定性是近似常 数。参见示图4. 不同类型的相机运动，深度噪声（即深度不确定性）如何作用在图像像素上（进 行加权）的。注意到的是，假设新图像帧的深度信息不可用，就不会定义新图像帧的尺度，然后就在 se(3)上进行最小化优化。

图示4：残差方差的统计归一化可视图示: （a）图像关键帧 （b）相机旋转 （c）相 机沿z轴平移（d）相机沿x轴平移，（b-d）被跟踪的图像帧和残差的逆方差 ，对于相机纯旋转运动，深度噪声对残差没有影响，因此所有归一化因子都是相同的。对于相机的轴向平移，深度噪声对图像帧靠中间的像素区域没有影响，对于 x 轴的相机平 移，仅影响 x 轴方向上强度梯度的残差。

3.4 深度图估计

关键帧的选择

创建新关键帧是根据相机移动距离来判断的，首先通过公式16.来计算当前关键帧和图像帧的加权距离，我们设置一个(当前关键帧和图像 帧的)距离阈值，（然后两者比较来判定是否触发新关键帧创建），其中， W 是包含权重的 对角（线矩）阵。

注意，在文章后续部分，每一个关键帧都被缩放了，以使得它们的平均逆深度为1，因此，这个距离阈值和当前场景的尺度是相关联的，并同时还要满足小基线立 体配准的要求。

深度图的创建

一旦新图像帧被选择成为关键帧，需要初始化它的深度图，即：把上一帧关键帧的兴趣点投影到新创建的关键帧上得到这一帧的兴趣点。然后进行兴趣点深度正则化以及外点移除，具体细节请参考论文[9]介绍。之后，深度图被平均至逆深度为1，并通过 sim(3) 变换缩放尺度因子。最后，这个关键帧替换前一帧关键帧，并视为接下来的图像跟踪参考帧，用于跟踪后续的新 图像帧。

深度图的优化

如果被跟踪的图像帧没有成为新的关键帧，那么就用来优化当前关 键帧如论文[9]中所述，对兴趣点图像区域，进行大量的小基线立体配准（作者这里略写，包括如 何选择参考帧，如何灰度误差匹配，计算几何误差，视差等等，详细流程，请参考论文[9]） 来更新深度。小基线立体配准的结果被更新到当前关键帧的深度图中，除了上述估计深度外，还要 计算深度的不确定性，修正深度，同时还会增加入新的像素点—这个过程使用了论文[9]中 的（卡尔曼）滤波方式来对深度的融合。

图示5：关键帧在 sim(3) 上的直接法配准：（a）—（c）两个（相邻）关键帧之间的 [相机]图像，深度图[估计]和深度方差可视化示图（d）—（f）[归一化的]光度测量残差，[归一化的]深度残差和Huber加权可视化示图，（左 侧）在最小二乘优化前的示图，（右侧）在最小二乘优化后的示图

3.5 图优化的边计算：sim(3) 直接法配准

单目SLAM 系统不同于RGB-D或双目SLAM — 具有尺度不确定性，即：场景的绝对尺度具有不可观性。所以，相机长距离的轨迹运动，会导致尺度漂移的问题，（即：尺度不确定性）是误差的主要产生原因之一，见论文[23]。此外，所有的距离计算都是取决于尺度，外点剔除或导致无法参数化核函数。我们通过利用场景深度（scene depth）和图像跟踪（配准）精度之间的内在相关性，来解决 这个问题：每个关键帧的深度图被缩放至它的平均逆深度是1。这样，就可以使用相似变换 sim(3) 来计算关键帧之间的边，因为相似 变换 sim(3) 可以较好地结合关键帧之间的尺度缩放差异，尤其是，针对大闭环，很容易地检测到累积的误差。

为此，我们设计一种新的算法，这个算法有如下特点：纠正尺度漂移，基于相似变换 sim(3)，直接法配准两帧（不同尺度缩放后的）关键帧。除了包含光度测量残差 rp ，我们还引入深度残差（depth residual） rd来惩罚关键帧之间的逆深度偏差，能直接够估计 出帧间的相似变换。那么误差函数E 的最小化优化项，就改写成如下公 式(17)，其中，光度测量残差 r2和它的方 差 σ2 的数学定义，请见公式（13）—（14）。

深度残差和它的方差计算分别如公式(18)和公式(19)，其中， ωs 是相似变换投影函数，p′ := ωs(p, Di(p), ξji) 是相似变换下转换到相机坐标系的点，（ Dj ([p′] ) 表示 p′ 对应关键帧 j 的深度， [p′]，这里用到第二章开头的数学符号定义 [⋅]

注意到，Huber范数作用在被归一化的光度测量残差和深度残差之和上—如果两个残差中有一项不收敛，另外一项也不收敛。还有，在 sim(3) 上的图像跟踪，需要包括深度误差，因为仅有光度测量误差是不足以限定尺度。和 se(3) 图像直接法类似， sim(3) 的最小化（优化问题）是通过加权高斯—牛顿迭代算法实 现的，请参考2.2小节。虽然 sim(3) 跟踪法比 se(3) 跟踪法的计算成本要大，但是在实际（代码实现）中，只是略微 增加小部分额外的计算量而已 1 。

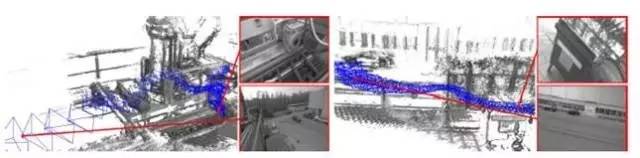
示图6. 尺度变化比较大的两个场景。 （蓝色椎体代表相机视锥，或相机镜头）每一个关键帧 上的相机视锥位姿在地图中被可视化（包括视锥尺寸大小和相应的关键帧尺度）。

约束条件检测.

当新的一个帧关键帧 Ki 添加地图之后，进行闭环检测，即收集可能是（形成）闭环的（候 选）关键帧 Kj1 , ..., Kjn 。为了检测大（尺度）闭环，我们使用最接近的十帧关键帧，以及由appearance-based mapping 算法[11] 筛选出来的候选帧。为了防止插入错误的或是假的闭环约束条件，我们要进行逆向相似度检测，即：

对每一帧闭环候选帧 Kjk ，我们独立去跟踪 ξjki 和 ξijk。只有当这两个变换估计在统计上很相似，例如：公式(20)的里面误差足 够小的情况下这样的闭环约束（边）才被加入到全局地 图里。为此，我们引入一个伴随矩阵（或叫邻接矩阵） Adjj i ，作用就是把 Σ转换到正确的切线空间。

收敛性分析

用直接法来配准存在一个很大的局限性，就是非凸性，因此需要足够准确的初始位姿。对于新图像帧的跟踪，可以由前一帧的相机姿态提供足够好的初始位姿，但是对于，找寻闭 环约束条件，它的初始预估位姿往往不会很准确，尤其是对长距离之后形成的大闭环来 说。有一种解决思路就是使用少量的图像特征点，计算获取更好的初始位姿估计：就是要配准两组已知对应关系的三维点云，其一，使用现有逆深度图的深度值，其二，使用四元素的封闭式解法，比如，Horn[13]提出的方法。然而，我们在实践中发现，即使对大闭环来说，收敛半径也是足够大 – 特别是我们发现，通 过以下方法可以显着增加收敛半径

• EMS方法：我们在[17]的工作中得到的（实验）结果论证，ESM在稠密（点云）图像配准的精度上不会 有明显增加， 但是会稍微增大一点收敛半径。

• 由粗到细配准的方法：直接法配准中经常使用到金字塔方法，（通过实验）我们发现，从非常低的分辨率开始，只 有20x15（像素）——远远小于通常做的（分辨率设置）——就已经有效提高收敛半径。

这些方法的评估实验报告，请详见4.3小节。

3.6 地图优化

地图是由关键帧作为节点和帧间sim(3)约束关系相连接构成的边组成，并且持续在后端通过姿态图优化进行修正。误差函数使用左乘规则（参见2.2小节），进行最小化（优化），这个误差函数定义如下：见 公式21.（ W 定义为世界坐标系）：

四. 实验结果

我们一方面通过现有公开的（离线）数据集[25,12]，另一方面（自己）用手持单目相机录制

室外大场景来获取相机轨迹，进行定量评估LSD-SLAM算法。部分评估的相机轨迹（请参考）补充视频，其中有完整显示。

4.1定性分析

我们控制摄像头进行一些长距离、高难度的轨迹运动来检测算法的性能，包括进 行多次旋转、大尺度变化以及大闭环运动等。示图（7）显示的是约500米的长距离轨迹，持续时间6分钟，在大回环闭合前后 的截图。示图（8） 显示的是场景深度变化大的相机运动轨迹，其中还包含闭环情况。

图示7：（顶部）显示的是难度较大的室外长距离SLAM（大）闭环（相机）轨迹示图（其中 左边是闭环之后的图示，右边是闭环之前的图示）。中间显示的是三个不同区域的半稠密局部点云地图特写，以及底部是对应的逆 深度在关键帧图像上的显示。

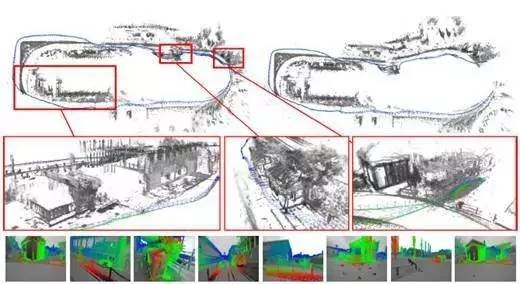
图8：（相机运动）轨迹叠加的（半稠密）点云地图，其场景深度的尺度变化大，平均逆深 度可以小到20厘米，大到可以超过10米。顶部示图左上角是闭环前的场景，两个红色圆圈表示同样的局部场景在地图中出现两 次，且尺度大小不同。右下角是大回环闭合之后的场景，使场景具有全局一致性。底部示图显示的是不同尺度下的局部场景特写。我们提出的方法，能够精确地估 计场景细节和具有大尺度的场景几何特征—这种灵活性是单目SLAM方法的主要优势之一。

4.2定量评估

我们通过现有RGB-D公开的数据集[25]来评估LSD-SLAM算法。值得注意的是，这个benchmark对单目SLAM来说很有挑战性，因为数据集里面包含相机的 快速旋转运动，强烈的动态模糊和滚动快门伪影效果等难点。我们通过最早的一帧关键帧上的深度图（初始化），来启动整个LSD-SLAM系统，并获得正 确的初始场景尺度。图表9罗列的是相机轨迹的绝对误差，并和其他SLAM算法比较精度的实验结果。

图示9：运行在TUM RGB-D 数据集 benchmark [25]上的结果，还包括两个[12]仿真图像序 列集，测量的绝对轨迹的标准误差（厘 米 cm）。图表中，我们在LSD-SLAM这一列还标注了关键帧的数量，’x’ 表示图像跟踪失败，’-’ 没有可 用的数据我们还使用其他四种算法来和LSD-SLAM算法比较，它们是：semi-dense mono-VO [9] keypoint-based mono SLAM [15] direct RGB-D SLAM [14] keypoint- based RGB-D SLAM [7]注意的是， [14] 和[7]使用RGB-D相机的深度信息，其他算法都是单目。

图示10：收敛半径和 sim(3) 直接法的精准度，配准过程中有/无ESM，分别用（亮色/暗色） 显示，不同的颜色表示使用的图像金字塔的层数。在第300帧（左边）和第500帧（右边）周围被跟踪到的图像帧，所有这些实验初始化是一样 的。底部显示了哪些帧跟踪成功（表述不确定，译者备注），顶部显示最终的平移误差。使用EMS和金字塔多层级可以增大收敛半径 的范围，但是对跟踪精度本身是没有特别的影 响。如果跟踪收敛成功，它几乎总是收敛到相同的最小值。

4.3收敛性评估

我们通过（TUM RGB-D benchmark）两个图像序列来评估收敛半径（convergence radius），实验结果请参看示图10。尽管直接法配准是个非凸性问题，但是通过实验表明根据3.5小节提出的算法步骤，我们 得到令人振奋的结果，即：相机大范围的运动也是能被跟踪的。我们还发现，这些策略，仅仅是 增大了收敛半径 的范围，对跟踪的精度本身是没有特别的影响。

五. 总结

我们提出了一种新颖的基于直接法的单目SLAM算法， 我们称之为LSD-SLAM，且这个单目SLAM系统,可以实时在单个CPU上运行。LSD-SLAM和其它现有，仅充当视觉里程计的直接法相比，它在全局地图上进行维护和图像 跟踪，这个全局地图包含由关键帧组成的姿态图，以及关键帧对应的用概率方式表现的半稠 密深度图组成。我们提出的方法的主要有两个创新点：

（1）两帧关键帧之间，用 sim(3) 直接法来配准，明确纳入和检测尺度漂移。

（2）一种新颖的概率方法，将深度图的噪声融合到图像跟踪中。地图以点云表示，其特点是，半稠密型而且是高精度的三维环境重构。

我们的实验表明，LSD-SLAM方法能够可靠地跟踪图像和构建地图，甚至能够成功挑战跟踪 超过500米长的运动轨迹，尤其是在同一图像序列中，场景尺度变化也比较大，（平均逆深度可以小到20厘米，大到可 以超过10米）,还出现相机的大旋转运动—展示了LSD-SLAM算法的多功能性，鲁棒性和尺度 的灵活性。

【参考文献】

1. Achtelik, M., Weiss, S., Siegwart, R.: Onboard IMU and monocular vision based

control for MAVs in unknown in- and outdoor environments. In: Intl. Conf. on

Robotics and Automation (ICRA) (2011)

2. Akbarzadeh, A., m. Frahm, J., Mordohai, P., Engels, C., Gallup, D., Merrell, P.,

Phelps, M., Sinha, S., Talton, B., Wang, L., Yang, Q., Stewenius, H., Yang, R.,

Welch, G., Towles, H., Nistr, D., Pollefeys, M.: Towards urban 3d reconstruction

from video. In: in 3DPVT. pp. 1–8 (2006)

3. Benhimane, S., Malis, E.: Real-time image-based tracking of planes using efficient

second-order minimization (2004)

4. Comport, A., Malis, E., Rives, P.: Accurate quadri-focal tracking for robust 3d

visual odometry. In: Intl. Conf. on Robotics and Automation (ICRA) (2007)

5. Concha, A., Civera, J.: Using superpixels in monocular SLAM. In: Intl. Conf. on

Robotics and Automation (ICRA) (2014)

6. Eade, E., Drummond, T.: Edge landmarks in monocular slam. In: British Machine

Vision Conf. (2006)

7. Endres, F., Hess, J., Engelhard, N., Sturm, J., Cremers, D., Burgard, W.: An

evaluation of the RGB-D slam system. In: Intl. Conf. on Robotics and Automation

(ICRA) (2012)

8. Engel, J., Sturm, J., Cremers, D.: Camera-based navigation of a low-cost quadro-

copter. In: Intl. Conf. on Intelligent Robot Systems (IROS) (2012)

9. Engel, J., Sturm, J., Cremers, D.: Semi-dense visual odometry for a monocular

camera. In: Intl. Conf. on Computer Vision (ICCV) (2013)

10. Forster, C., Pizzoli, M., Scaramuzza, D.: SVO: Fast semi-direct monocular visual

odometry. In: Intl. Conf. on Robotics and Automation (ICRA) (2014)

11. Glover, A., Maddern, W., Warren, M., Stephanie, R., Milford, M., Wyeth, G.:

OpenFABMAP: an open source toolbox for appearance-based loop closure detec-

tion. In: Intl. Conf. on Robotics and Automation (ICRA). pp. 4730–4735 (2012)

12. Handa, A., Newcombe, R., Angeli, A., Davison, A.: Real-time camera tracking:

When is high frame-rate best? In: European Conference on Computer Vision

(ECCV) (2012)

13. Horn, B.: Closed-form solution of absolute orientation using unit quaternions. Jour-

nal of the Optical Society of America (1987)

14. Kerl, C., Sturm, J., Cremers, D.: Dense visual SLAM for RGB-D cameras. In:

Intl. Conf. on Intelligent Robot Systems (IROS) (2013)

15. Klein, G., Murray, D.: Parallel tracking and mapping for small AR workspaces. In:

Intl. Symp. on Mixed and Augmented Reality (ISMAR) (2007)

16. Klein, G., Murray, D.: Improving the agility of keyframe-based SLAM. In: Euro-

pean Conference on Computer Vision (ECCV) (2008)

17. Klose, S., Heise, P., Knoll, A.: Efficient compositional approaches for real-time

robust direct visual odometry from RGB-D data. In: Intl. Conf. on Intelligent

Robot Systems (IROS) (2013)

18. Kümmerle, R., Grisetti, G., Strasdat, H., Konolige, K., Burgard, W.: g2o: A general

framework for graph optimization. In: Intl. Conf. on Robotics and Automation

(ICRA) (2011)

19. Li, M., Mourikis, A.: High-precision, consistent EKF-based visual-inertial odome-

try. International Journal of Robotics Research 32, 690–711 (2013)

20. Newcombe, R., Lovegrove, S., Davison, A.: DTAM: Dense tracking and mapping

in real-time. In: Intl. Conf. on Computer Vision (ICCV) (2011)

16 J. Engel and T. Schöps and D. Cremers

21. Pizzoli, M., Forster, C., Scaramuzza, D.: REMODE: Probabilistic, monocular dense

reconstruction in real time. In: Intl. Conf. on Robotics and Automation (ICRA)

(2014)

22. Schöps, T., Engel, J., Cremers, D.: Semi-dense visual odometry for AR on a smart-

phone. In: Intl. Symp. on Mixed and Augmented Reality (ISMAR) (2014)

23. Strasdat, H., Montiel, J., Davison, A.: Scale drift-aware large scale monocular slam.

In: Robotics: Science and Systems (RSS) (2010)

24. Stühmer, J., Gumhold, S., Cremers, D.: Real-time dense geometry from a handheld

camera. In: Pattern Recognition (DAGM) (2010)

25. Sturm, J., Engelhard, N., Endres, F., Burgard, W., Cremers, D.: A benchmark

for the evaluation of RGB-D SLAM systems. In: Intl. Conf. on Intelligent Robot

Systems (IROS) (2012)

在微信后台回复“20170821”，获得英文全文。