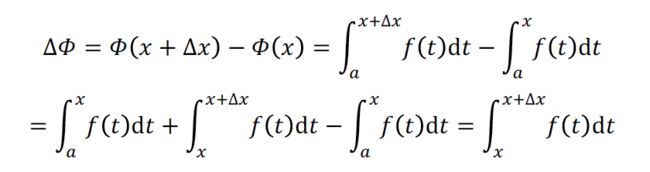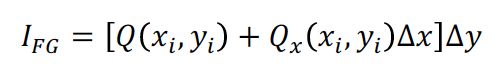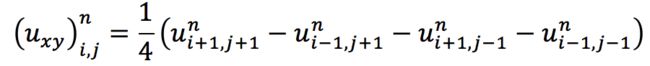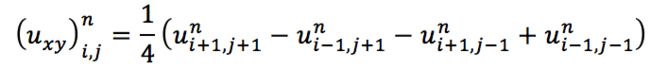图像处理中的数学修炼的特别说明及其勘误表
由清华大学出版社出版的《图像处理中的数学修炼》这本书是今年3月左右正式上市销售的。现在三个多月过去了,已经积累了大量的读者。但是,随着读者数量的增加,近来有部分读者在跟我交流和咨询的时候表现出来许多在读书和用书时的困惑,这里我特别把这本书的一些情况和大家可能有的误解在做一个澄清,希望大家对这本书的结构、作用、意义和阅读的方法有一个了解,从而真正发挥它的作用。同时也避免潜在读者由于错误地使用本书而使得自己事倍功半、收效不及预期的情况发生。
![]()
如果你是这本书的读者或者准备购买本书的潜在读者,请你务必了解下面这些内容:
这本《图像处理中的数学修炼》全书一共八章,可分为两个部分,前四章全部是数学原理,并不涉及任何具体的图像处理算法,后四章是数学在图像里的应用。
你可能会讶异,如果前四章都是不涉及图像处理的纯数学知识,那我何不直接买一本数学书?这里特别需要说明,前四章的意义在于:图像处理往深了研究,需要用到大量的数学知识,但是你不可能把数学专业的教材全借来从头到尾学一遍,那样你精力也不够用。
本书前四章,是从各种数学领域挑出来跟图像研究最直接相关,也就是你最需要,最可能会用到的数学知识,所以这部分的意思在于给你限定了一个范围,就像考试之前画重点一样。如果这些数学知识你都掌握了,那么图像处理算法中涉及的所有公式你就都能看懂了。
当然只有理论你肯定会觉得空洞。所以为了锻炼你应用前4章数学知识的能力我特别安排了后4章。后四章里会大量用到前4章里的数学概念,例如梯度,散度,黑塞矩阵,高斯迭代法,欧拉-拉格朗日公式等等,但是后面不会再解释这些数学概念,因为前4章里面已经讲过了。后4章的作用就在于让你巩固一下前面所学,然后自己实际感受一下这些数学的用武之地。
但是我不可能把一整本图像处理书所有的东西都拿来做例子,因为毕竟篇幅有限。所以后四章就相当于攫选了图像处理中的四个大的Topics来讲解,当然细分的话可能包括很多具体的算法(例如直方图均衡、暗通道去雾、基于频域变换的图像压缩等等)。所以后4章并不能覆盖所有图像的话题,也不需要覆盖,例如可能图像处理中用到黑塞矩阵的地方有超过十个算法,作为例子我讲一两个也就足够了。后4章只是帮你巩固和体会前面数学知识在图像处理中的应用。所以你不能通过阅读《数学修炼》这本书来掌握图像处理的所有话题,也不能用它来作为图像处理的入门。但是你可以把这本书作为你学习图像处理中所需要的数学基础的一个指导。此外,我觉得在日后的研究中把它作为一本字典来用也是很不错的选择。
------------------------------以下是勘误表部分-----------------------------------
《图像处理中的数学修炼》一书已由清华大学出版社出版发行。勘误表请见如下(不断更新中):
关于本书的更多详情及目录可以参见 http://blog.csdn.NET/baimafujinji/article/details/48467225 。
* 表示第二次增印中已经改正。
** 表示第三次增印中已经改正。
*** 表示第四次增印中已经改正。
* 1、前言部分,第1页,最后1段第1行:总所周知,... ...
应该改为:众所周知
** 2、第1章,第12页:“通过计算可知”下面的公式中无端多出了一个4,应该改为:
* 3、第1章,第18页:在第2章中,本书还会讨论勒贝格... ...
应该改为:在第3章中,本书还会讨论勒贝格... ...
* 4、第1章,第21页:“由此得函数的增量”后面公式的积分下限有误,应该改为:
* 5、第1章,第22页:内积的性质:a、b 是两个向量,... ...
应该改为:a、b 和 c 是三个向量
* 6、第1章,第24页:(a · b) × c = a · (b + c)
应该改为:(a · b) × c = a · (b × c)
* 7、第1章,第24页:(a × b) × c + b × (c × a) + c × (a × b) = 0,第一个括号加错位置了,应该改为:
* 8、第1章,第25页:这里 grad f(x,y), e 表示向量 grad f(x,y) 与 e 的夹角,应该改为:
特别说明:一般教材上会使用尖括号<a,b>来表示向量 a 和 b 的夹角,而本书中采用的符号是小括号。为保证全书统一,这里仍然使用小括号。
** 9、第1章,第33页,“所以,可得”下面的公式印刷有误,应该改为:
* 10、第2章,第52页,“对于第二个等式,... ... ” 下面的公式中有 sim
应该改为:sin
** 11、第2章,第88页,“回想第1章中介绍的黑塞矩阵... ... ”后面的公式中,通常大写粗体表示矩阵,
其中的 X 其实是向量(而非矩阵),为保持与本书其他地方一致,应该把其中涉及到的 X 都改成 x。
* 12、第2章,第94页,“但并不需要以矩阵形式存储A”,既然是矩阵,则应该使用大写粗体,
应该改为:A
* 13、第3章,第110页,闵可夫斯基(Minkowski)不等式中字母 a 的上下标印刷错误,应该改为:
* 14、第3章,第143页,一共有5个 div,
为了保持全书统一,应该改为粗体:div
* 15、附录,第420页:在本书的后面,也会给出... ...
应该改为,在本书的前面,也已经给出过
** 16、第3章,第129页,“欧拉-拉格朗日方程(euler-Lagrange equation)... ...”
人名应大写,所以应该改为:“欧拉-拉格朗日方程(Euler-Lagrange equation)... ...”
** 17、第1章,第15页,“如果二阶导数 f '(x) < 0... ...”
应该改为,“如果二阶导数 f ''(x) < 0... ...”
** 18、第7章,7.3.3节,公式
应该改为:
*** 19、第4章,第200页,,P(X)=P(X|θ=0.5)+P(X|θ=0.8),根据全概率公式,应该改为:
P(X)=P(X|θ=0.5)⋅P(θ=0.5)+P(X|θ=0.8)⋅P(θ=0.8)
*** 20、第6章,图6-3,最右侧,F(1) F(2) F(3) F(4) F(4) F(5) F(6) F(7),应该改为:
F(0) F(1) F(2) F(3) F(4) F(5) F(6) F(7)
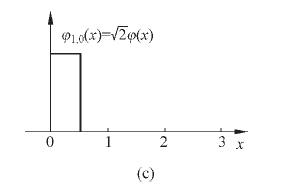
*** 21、P252页图31的c
表达式括号中内容有误,应为2x,即
*** 22、P247页,
平方误差为后面的值有误,应该改为:
*** 23、P176,“CDF反函数(及分位数函数)”
应该改为,“CDF反函数(即分位数函数)”
*** 24、P177,第一行,“图4-8所示的关系”
应该改为,“图4-9所示的关系”
*** 25、P177, 图4-9中,Mq(x)是相乘的关系,所以q不应该写成下标的形式
如果你在阅读本书过程中,发现任何问题,也欢迎反馈给我(可以在本博客留言或者发邮件给我),感谢你为本书的改进所做的贡献。