深度学习与视频编解码算法一
论文《Variational image compression with a scale hyperprior》
大牛Johannes Ballé写的,必须要读。
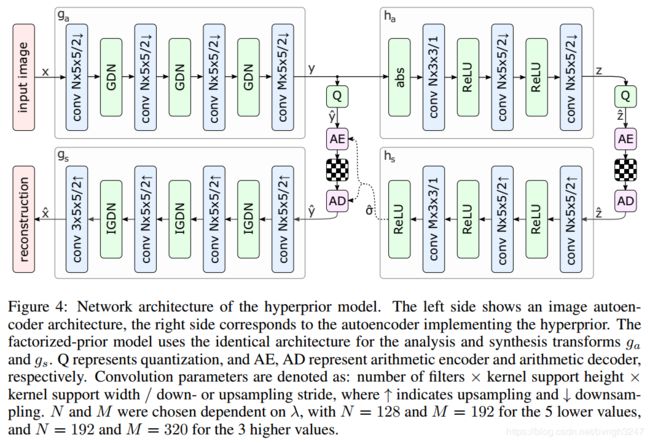
通过自编码器把图像压缩成latent representation(大小变为原始图像1/16 * 1/16)
然后把latent representation通过统计概率使用熵编码进行编码。
在熵编码由于不知道真实的字符概率,所以需要可以统计这些信息,可以把这些信息传到解码端。
在训练中采用端到端的训练,需要把平衡side信息与熵模型的提升。以达到总体的码字编码降低。
训练时,由于量化引入了误差,使用梯度下降无法进行,因此把量化当作是均匀噪声。
由于latent representation具有分布特性,因此引入条件Z(概率分布情况),使用它来压缩图像, 通过编码端传递到码流中,然后解码端根据Z得到latent representation分布,进而得到重新图像。如下图中的右边部分。
熵编码
Cumulative distribution function累积分布函数(cdf)
累积分布函数(cumulative distribution function)定义:对连续函数,所有小于等于a的值,其出现概率的和。F(a)=P(x<=a)

参考:https://blog.csdn.net/sinat_26599509/article/details/52882769
y_tilde, likelihoods = entropy_bottleneck(y, training=True)
训练主要调用entropy_models.py文件中函数 def call(self, inputs, training),其中主要是对y 加上noise得到y_tilde.
以及对y_tilde计算累积概率,进而得到 likelihoods(似然估计)值。
边缘概率分布(the marginal distribution)
某一组概率的加和,叫边缘概率。边缘概率的分布情况,就叫边缘分布。和“边缘”两个字本身没太大关系,因为是求和,在表格中往往将这种值放在margin(表头)的位置,所以叫margin distribution。
marginal distribution,边缘分布(有时也翻译成边界分布)。
如果我们把每一个变量的概率分布称为一个概率分布,那么边缘分布就是若干个变量的概率加和所表现出的分布。举个例子,假设P(B),P©,P(A|B),P(A|C)已知,求P(A)。那么P(A)=sum(P(B)*P(A|B),P©*P(A|C))。
再举个简单的例子:对于一个任意大小(n*n)的概率矩阵X,每一个元素表示一个概率,对于其中任一行或任一列求和,得到的概率就是边缘概率。如果写成式子,就是第i行有以下边缘分布:P(i)=sum(P(i,j),for each j in n)。
- PDF:概率密度函数(probability density function), 在数学中,连续型随机变量的概率密度函数(在不至于混淆时可以简称为密度函数)是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。本身不是概率,取值积分后才是概率。
- PMF: 概率质量函数(probability mass function), 在概率论中,概率质量函数是离散随机变量在各特定取值上的概率。
- CDF: 累积分布函数 (cumulative distribution function),又叫分布函数,是概率密度函数的积分,能完整描述一个实随机变量X的概率分布。是PDF在特定区间上的积分。 CDF就是PDF的积分,PDF就是CDF的导数.

这个函数即是模拟概率分布函PMF,这些参数是预先训练得到,表示每一个可能值的概率。例如128值的分布概率最高。具体计算方法如下:
lower = self._logits_cumulative(samples - half, stop_gradient=True)
upper = self._logits_cumulative(samples + half, stop_gradient=True)
# Flip signs if we can move more towards the left tail of the sigmoid.
sign = -math_ops.sign(math_ops.add_n([lower, upper]))
pmf = abs(math_ops.sigmoid(sign * upper) - math_ops.sigmoid(sign * lower))
# Add tail masses to first and last bin of pmf, as we clip values for
# compression, meaning that out-of-range values get mapped to these bins.
pmf = array_ops.concat([
math_ops.add_n([pmf[:, 0, :1], math_ops.sigmoid(lower[:, 0, :1])]),
pmf[:, 0, 1:-1],
math_ops.add_n([pmf[:, 0, -1:], math_ops.sigmoid(-upper[:, 0, -1:])]),
], axis=-1)
通过PMF可以计算得到CDF累计分布。通过这个可以调用range_decode就可以进行码字的编码与解码。
cumFreq0 = [0, 4, 5, 6] //表示累记频率。
sequence = [0, 0, 0, 0, 1, 2; 0, 0, 0, 0, 1, 2; 0, 0, 0, 0, 1, 2]
encoder.encode(data0, sequence )
论文《end-to-tend optimized image compression》
如下图所示,通过优化 R + lambda * D 值,即使编码端与解码端优化对应的参数。

对于量化,采用一个损失函数来代替(proxy loss function based on a continuous relaxation of the probability model),防止梯度为0.
实现一个真实的码率输出bit数目,加入到训练中,这是一个最大的创新点。码率的输出采用Dirac delta functions函数,即
码率的大小决定下面的字符分布统计,如果分布越集中,码率越小。这个需要训练得到对应的参数。

量化损失是与码就有关:
变换是为了减少数据的相关性,在变换过程中采用归一化,能够提高性,因此提出了generalized divisive normalization(GDN)变换。
y_tilde, likelihoods = entropy_bottleneck(y, training=True) 此片主要是对Y加噪声得到y_tilde,以及得到分布概率,进而计算出码率。由于量化部分维度非常高,我们采用了正布分布的噪声来代替。
训练时,分为二部分损失
train_mse = tf.reduce_mean(tf.squared_difference(x, x_tilde))
train_mse *= 255 ** 2
train_bpp = tf.reduce_sum(tf.log(likelihoods)) / (-np.log(2) * num_pixels)
train_loss = args.lmbda * train_mse + train_bpp //rdo损失
entropy_bottleneck.losses[0] //熵相关部分损失,这部分还没有理解清楚,估计是熵重建损失。
entropy_bottleneck.updates[0]//还没有理解清楚。
train_op = tf.group(main_step, aux_step, entropy_bottleneck.updates[0])
把这三部分联合在一些一起训练,同时进行减少。
由于训练时量化时梯度为 0,因为使用uniform noise来代替量化过程,有利于数据的训练。