应用举例11.6 哈夫曼编码（单调队列 or 优先队列）

---

1，问题描述

每一个单词有一个频率，构造一个压缩算法使其带权路径和最小（叶子节点的频度*深度的累加），并输出每个单词的压缩编码。

---

2，思路

建树

贪心构造哈夫曼树的经典压缩算法，以下写几种建树实现的算法：

暴力枚举构造

因为每次要选取2个当前最小的构成一个小的分支，这两次搜索可以去链表中摘两个最小的块封装成哈夫曼树并放回链表中，迭代n-1次即可，算法复杂度$O(n^2)$。具体实现看戳这里。

优先队列(极小堆)

由于每次要贪心地选取两个花费最小的元素，并再次入选取集。抽象一下就是push和pop两个操作，于是可以用小根堆即可，复杂度会是一个常数较大的$O(nlogn)$

单调队列

建立两个空的单调队列，对于n个单词及其频度我们可以预先对其排个序，之后放入一个单调队列中，之后维护这两个单调队列，具体操作如下：

• 假设初试时满的单调队列是q，空的单调队列是p
• 我们还要再定义一个单调队列mq用于存放2个选取后的节点
• 当mq不足两个元素时，每次从p，q队头取一个最小的元素加入mq
• 当mq有两个元素后把两个取出封装后放回队列p中
• 整个算法运行知道p、q均为空哈夫曼树建立完成

以上说的单调队列实际上不是我们人为维护的一个单调队列，因为预先排了序，故每次选两个加到p队列队尾一定能保证p单调不减(没有频度为负数)，因为如果你发现某两次合并的节点小于于p的堆尾说明了之前那个节点合并一定不是选取最小的，但我们操作又是取最小的，故不会发现上述这种情况。而q显然是预处理单调不减的队列，所以每次选取的队头最小一定是当前全局的最小数，所以就能在$O(1)$时间内找到两个最小的节点进行合并。所以这种算法的复杂度的主部是排序部分$O(nlogn)$，建树部分则是$O(n)$，当然如果你有比较好的基数排序算法或者桶排序则能够将复杂度降为线性时间。

双指针

实际上就是对单调队列数组上的实现方式

堆结构

开一个$2\ast n$的数组，每个元素有一个父亲指针以及两个孩子节点指针和该节点的频度权值。把要合并的n个节点放到$[1,n]$中，其余的初始化为0。从$[n+1,2\ast n-1]$进行建立哈夫曼树，具体操作如下：
从[1,i-1]找两个权值非0的孩子节点父亲指针指向i，i的孩子指针分别指向两个，两个孩子节点的权值设为0（表示已经选取），而父亲节点的权值变成两个孩子节点的累和。迭代n-1次后2n-1下标的节点即为哈夫曼树的根。复杂度$O(n^2)$

---

编码

对于编码有递归和非递归两种算法，而非递归有从底向上也有自定向上的算法：

递归

自顶向下，变量到叶子节点时输出编码，往左分支在编码后加0，往右分支则加1或者相反。以上几种结构无论是链型或者是堆形都有二叉树的特征故都适用

非递归

自底向上

这种遍历模式只适用于顺序的堆结构，链结构由于没有父亲指针以及所有叶子节点指针表，故不适用。具体的思路是对于建立的哈夫曼树，也就是那个表，从[1,n]的节点每次往上溯源即可，而每次要判断一下当前节点是父亲节点的左孩子还是右孩子进行头插编码。迭代n次得到n个编码。

自定向下

根据二叉树非递归先序的思路设一个标记为数组，0表示该分支没遍历过，则说明是左分支，尾插编码集后进入左孩子节点编号迭代，并将该数设位1，同理当为1时则进入右孩子节点…标记编号设为2，若为2时则要进行回溯，帮当前cur通过父亲指针回到上一级节点，同时编码集要记得-1，这是伴随着回溯的重要操作！

---

3，实现

以下为单调队列算法构造哈夫曼树，递归编码并计算带权路径和的实现：

#include 
using namespace std;

class BiTree;
class Dict;
class HuffmanTreeNode;

template<class T>
class BiTreeNode {
protected:
    T* lson, *rson;
public:
    BiTreeNode(T* ls, T* rs):lson(ls), rson(rs) {}
    BiTreeNode():lson(NULL), rson(NULL) {}
    ~BiTreeNode() {
        if(lson) delete lson;
        if(rson) delete rson;
    }
};

class Dict {
protected:
    string word;
    int size;
public:
    Dict() {}
    Dict(string wo, int si):word(wo), size(si) {}
    string getWord() {return word;}
    int getSize() {return size;}
};

class HuffmanTreeNode:public BiTreeNode<HuffmanTreeNode>, public Dict {
public:
    HuffmanTreeNode(Dict& elem):BiTreeNode<HuffmanTreeNode>(), Dict(elem.getWord(), elem.getSize()) {}
    HuffmanTreeNode(HuffmanTreeNode* ls, HuffmanTreeNode* rs):BiTreeNode<HuffmanTreeNode>(ls, rs) {
        this->size = ls->getSize() + rs->getSize();
    }
    HuffmanTreeNode* getLchild() {return this->lson;}
    HuffmanTreeNode* getRchild() {return this->rson;}
    ~HuffmanTreeNode() {
        if(this->getWord().empty()) cout << this->getSize() << endl;
        else {
            cout << this->getSize() << ' ' << this->getWord() << endl;
        }
        nodeCount ++;
    }

    static int nodeCount; //删除结点计数器
};

int HuffmanTreeNode::nodeCount = 0;

void previsitHuffmanTree(HuffmanTreeNode* rt, string str) //先序访问huffman树,结点编码
{
	if(rt==NULL)
		return ;
	else if(rt->getLchild()==NULL && rt->getRchild()==NULL)
	{
		cout << "单词:" << rt->getWord() << " 频数:" << rt->getSize() << " 编码:" << str << endl;
		return ;
	}
	str.push_back('1');
	previsitHuffmanTree(rt->getLchild(), str);
    str.back() = '0';
	previsitHuffmanTree(rt->getRchild(), str);
    str.pop_back();
	return ;
}

unsigned int HuffmanWPL(HuffmanTreeNode* T,unsigned int L)
{
	if(T==NULL)
		return 0;
	else if(T->getLchild()==NULL && T->getRchild()==NULL)
		return T->getSize()*L;
	return HuffmanWPL(T->getLchild(),L+1)+HuffmanWPL(T->getRchild(),L+1);
}

vector<Dict*> vect;
queue<HuffmanTreeNode*> q,p; //维护权值的单调队列

int main() {
    int n;
    string str; int size;
    vect.clear(); 
    while(!q.empty()) q.pop();
    while(!p.empty()) p.pop(); 
    cin >> n; //输入n个单词
    for(int i=0; i<n; i++) {
        getchar();
        getline(cin, str, '\n');
        cin >> size;
        vect.push_back(new Dict(str, size));
    }
    sort(vect.begin(), vect.end(), [](Dict* a, Dict* b){return a->getSize() < b->getSize();}); //把频度排序
    for(int i=0; i<vect.size(); i++) q.push(new HuffmanTreeNode(*vect[i])); //构造单调队列
    
    HuffmanTreeNode *v1, *v2;
    queue<HuffmanTreeNode*> mq; while(!mq.empty()) mq.pop();
    while(!q.empty() || !p.empty() || mq.size() > 1) {
        if(mq.size() < 2) { //还不够2个则到队列中取
            //两个队列都有取一个最小的入队
            if(q.empty() || !p.empty() && p.front()->getSize() < q.front()->getSize()) {
                v1 = p.front(); p.pop();
            } else {
                v1 = q.front(); q.pop();
            }
            mq.push(v1);
        } else { //已有两个进行合并
            v1 = mq.front(); mq.pop();
            v2 = mq.front(); mq.pop();
            p.push(new HuffmanTreeNode(v1, v2));
        }
    }

    str.clear();
    v1 = mq.front(); mq.pop();
    cout << v1->getSize() << endl;
    printf("\n先序遍历HuffmanTree结点编码:\n");
	previsitHuffmanTree(v1, str);
    printf("\nHuffmanTree的带权路径长度:\n");
	printf("%u\n", HuffmanWPL(v1, 0));
    printf("\n递归删除HuffmanTree的结点:\n");
    HuffmanTreeNode::nodeCount = 0;
    delete v1;
    printf("\n共删除%d个结点\n", HuffmanTreeNode::nodeCount);
    return 0;
}

/*
15
The
1192
of
677
a
541
to
518
and
462
in
450
that
242
he
195
is
190
at
181
on
174
for
157
His
138
are
124
be
123
*/

---

4，拓展

哈夫曼树建立的每个节点都是一个满的结构，如果问题是建立一个k叉的哈夫曼树该如何做呢？根据哈夫曼树的思路如果每次贪心选取前k小可能会得到一个这样的结构：
假如6个节点：{2,2,2,3,3,3}

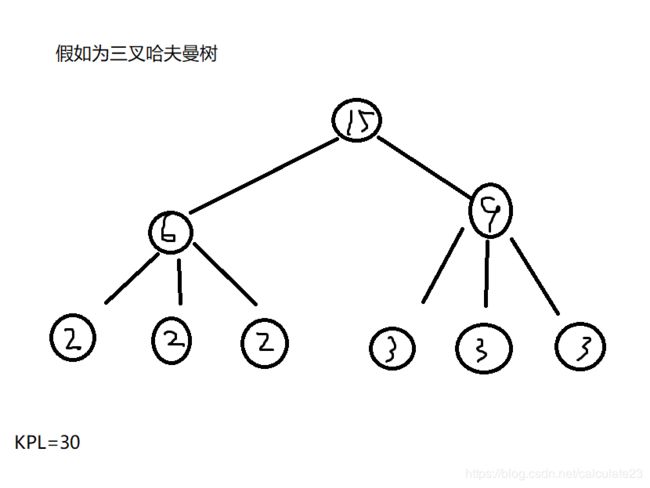
但我们却能够寻找到这样的一个结构：

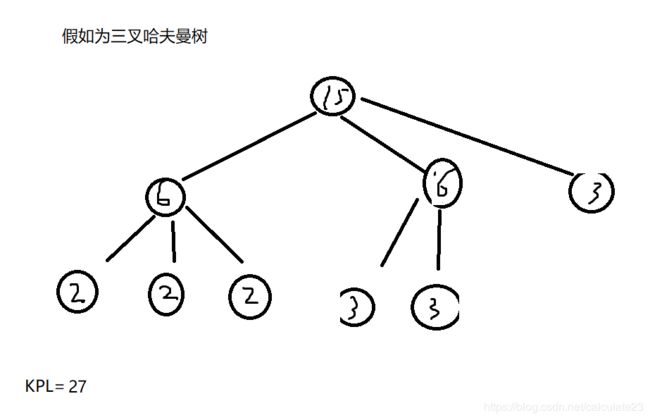
正确构造K叉哈夫曼树是补上若干个0节点使其能在不会影响整个树的权值的情况下形成k叉满二叉树。

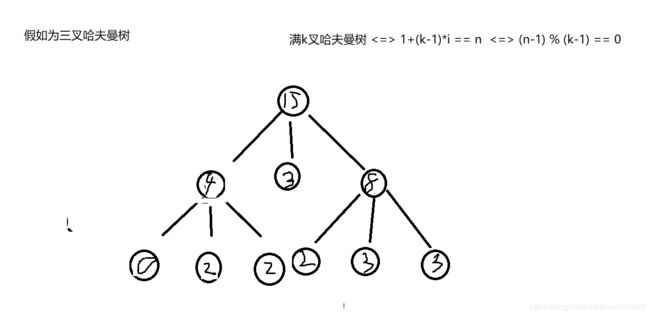
关于实现可以每次找k个最小的时候进行判断也可以实现补上这些0结点，公式是$(n-1)\%(k-1)==0$

公式推导：
最终的状态一定是只有一个结点即$dp[1]=1$，假设当前状态为dp[i]，则上一个合并执行完的状态一定是dp[i]=dp[i-1]+(k-1)。所以每次在前一个基础上加上$k-1$最终的状态是$s\ast (k-1)+1==n$，则移项一下就是$(n-1)\%(k-1)==0$就是最终的状态。

---

5，注意

关于哈夫曼树的带权路径和KPL是叶子节点的频度乘上深度，不要写成整个链上的每个结点求和（树上前缀和）。