生成树计数——矩阵树定理(Matrix-Tree)

结论

实际上求得的是每个生成树边权乘积的总和

无向图

对于无向图$G$，设第$i$个点的度数为$d_i$，第$i$个点与第$j$个点相连的边数为$a_{ij}$ 。
定义$G$的基尔霍夫矩阵$L_G$ 为：当$i̸=j$时，$l_{ij}=-a_{ij}$；当$i=j$，$l_{ii}=d_i$。
定义$M_{ij}$为矩阵$L_G$删除第$i$行和第$j$列后的矩阵（即$L_G$的$l_{ij}$余子式）。
当$i=j$时，称$M_{ii}$为$L_G$的主余子式。

则图$G$的生成树个数为任意一格主余子式$M_{ii}$的行列式的绝对值。

有向图

对于有向图$G$，设第$i$个点的除去自环后的入度为$d_i$，第$i$个点与第$j$个点相连的边数为$a_{ij}$
。
定义$G$的基尔霍夫矩阵$L_G$ 为：当$i̸=j$时，$l_{ij}=-a_{ij}$；当$i=j$，$l_{ii}=d_i$。
定义$M_{ij}$为矩阵$L_G$删除第$i$行和第$j$列后的矩阵（即$L_G$的$l_{ij}$余子式）。
当$i=j$时，称$M_{ii}$为$L_G$的主余子式。

则图$G$的以点$i$为根的生成树个数为主余子式$M_{ii}$的行列式的绝对值。

带权图

设第$i$个点与第$j$个点相连的边权为$a_{ij}$
定义$G$的基尔霍夫矩阵$L_G$ 为：当$i̸=j$时，$l_{ij}=-a_{ij}$；当$i=j$，$l_{ii}=\sum _{k=1,k̸=i}^n{a}_{ik}$。

口胡Matrix-Tree证明

前置技能

行列式

定义

对于$n$阶方阵$A$
$$A=\left\{\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right\}$$
它的行列式$D$为
$$D=|A|=\sum _S(-1{)}^k{a}_{1,S_1}\cdot a_{2,S_2}\cdot a_{3,S_3}...a_{n,S_n}$$
$s$为1~n的排列，$k$为此排列的逆序对数。
所以

初等变换

• 这种矩阵：$$A=\left\{\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ 0& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & a_{nn}\end{array}\right\}$$
  即左下角都是0，$|A|={\prod }_{i=1}^n{a}_{ii}$
  （相当于只用$S=1,2,3,4,...,n$才有值，其它S都会扯到左下方的0）
• 将矩阵的两行或两列交换，行列式的值$\times (-1)$。（可以理解为：对于每个$S$，逆序对数都变化了1）
• 将矩阵的一行或一列全部乘以常数$p$，行列式的$\times p$。
• 将矩阵的一行或一列全部乘以常数$p$，再加到另一行（列）上去，行列式的值不变。
• $$\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ ⋮& ⋮& & ⋮\\ a_{i1}+b_{i1}& a_{i2}+b_{i2}& \cdots & a_{in}+b_{in}\\ ⋮& ⋮& & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right|=\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ ⋮& ⋮& & ⋮\\ a_{i1}& a_{i2}& \cdots & a_{in}\\ ⋮& ⋮& & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right|+\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ ⋮& ⋮& & ⋮\\ b_{i1}& b_{i2}& \cdots & b_{in}\\ ⋮& ⋮& & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right|$$
  这几个性质可以用下面这个公式（拉普拉斯展开）证明。

拉普拉斯展开

对方阵$A$的第$i$行进行展开：
$$D=\sum _{j=1}^n(-1{)}^{i+j}{a}_{ij}{M}_{ij}$$
可以理解为将$a_{ij}$经过$i+j$次交换移动到第一行第一列去，再计算。

行列式求法

用类似（几乎一模一样）高斯消元的方法，将矩阵用前面那一坨性质消成上三角型，然后把对角线乘起来，记录一下交换行的次数，判断要不要乘-1即可。

柯西-比尼定理（Cauchy-Binet）

对于一个$n\times m$ ($n\le m$)的矩阵$A$，和$m\times n$的矩阵$B$，
$$|AB|=\sum _{|s|=n}|A_{\ast s}{B}_{s\ast }|$$
$s$为$1,2,3,...,m$的大小为n的子集，$A_{\ast s}$选s集合中的列组成的方阵，$B_{s\ast }$表示只选s中的行组成的方阵。

证明略 （不会证）

Matrix-Tree定理证明

基尔霍夫矩阵性质

基尔霍夫矩阵行列式为0

可以发现，基尔霍夫矩阵中，每一列的和一定为0
用行列式的性质，可以把所有行都加到其中一行上，这一行就全部为0，则行列式就为0了。
所以基尔霍夫矩阵的行列式为0。

不连通的图的主余子式行列式为0

对于不连通的图，其基尔霍夫矩阵，可以通过若干次交换行或列，得到以下形式：
(0表示一个全0的矩阵，$L_{G_i}$为第i个连通块的基尔霍夫矩阵）
$$L_G=\left\{\begin{array}{cccc}{L}_{G_1}& 0& \cdots & 0\\ 0& L_{G_2}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & L_{G_k}\end{array}\right\}$$
如果图不连通，则存在多余1个的$L_{G_i}$，不论主余子式删除的是哪一行那一列，都存在一个连通块的$L_{G_i}$保证完整，通过变换，可以使某一行变为全0，则这个主余子式的行列式为0。

树的主余子式为1

将树的结点按深度从小到大重新标号，并且使主余子式删掉的编号$i$为当前的根。

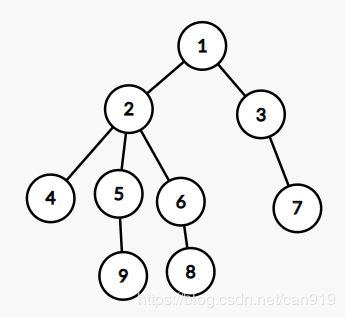
设一个编号为$u$的叶子结点，它的父亲结点编号为$v$。则主余子式上第$u$行一定为这个样子：$l_{uv}=-1(v<u,v̸=1),l_{uu}=1$，其余全为0。
则从主余子式的最后一行开始（此时这一行一定为叶子），将这个叶子结点的父亲那一行，减去当前这一行，然后删掉这个叶子结点。
当一个结点$u$的儿子被删完后，这个结点就变成新的叶子结点，且在主余子式上也变为这种形式：$l_{uv}=-1(v<u,v̸=1),l_{uu}=1$，其余全为0。
直到只剩下1的儿子结点。
通过这样的转化，使得主余子式变为下三角形，且对角线上全部为1。
所以它的行列式也为1。

关联矩阵

定义图$G$的关联矩阵$B$为：对于一条编号为$i$的边$(u_i,v_i)$，则$B_{i,u_i}=1,B_{i,v_i}=-1$
关联矩阵是$m\times n$的，$n$为点数，$m$为边数。
定义$B$的转置矩阵为$B^T$。
可以得出$B{B}^T=L_G$，直接把矩阵乘法的式子写出来可以轻松证明。

证明主体

定义$B_i$表示关联矩阵删去第$i$列的矩阵。
则$$|M_{ii}|=|B_i^T{B}_i|$$
由柯西-比尼定理得
$$M_{ii}=|B_i^T{B}_i|=\sum _{|s|=n-1}|(B_i^T{)}_{s\ast }(B_i{)}_{\ast s}|$$
观察发现$s$，即为选择的边的集合
如果选的边的集合导致图不连通，由之前的证明得到，它的行列式为0。
如果选的边连通，则构成一颗树，它的行列式为1。

于是$M_{ii}$就相当于枚举所有边的树，并记下了方案数。

证毕