【总结】插头DP-bzoj1210/2310/2331/2595

首先感谢LadyLex的插头DP：从零概念到入门，让我对插头DP的理解更进了一步。本文部分内容/图片也转录于此。

---

概述

插头DP主要用来处理一系列基于连通性${}_1$状态压缩${}_2$ 的动态规划问题，处理的具体问题有很多种，并且一般数据规模较小。

插头DP在棋盘模型上的应用最广泛，非常考察思维的严谨性和全面性。

在基本的模板(哈希/DP结构)的基础上，插头的变换和衔接成为了问题的关键。

---

基本方式

状态确定

插头

在插头DP中，插头表示一种联通的状态，以棋盘为例，一个格子有一个向某方向的插头，就意味着这个格子在这个方向已经与外面相连（表示两个相邻格子之间已经格子联通）。

前驱状态对应的插头必须接上，同时考虑接下来插头的走向。

逐格递推

对于第$i$行第$j$列的格子$(i,j)$：走向它的方案，可能由上一行的下插头转移而来，也可能是本行的右插头转移而来。

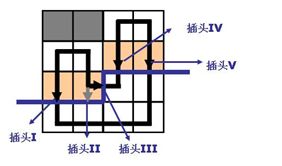
一如轮廓线DP，插头$DP$用状态压缩的方式记录处理当前格时最近一排已决策格子的插头情况。具体而言：$1$~$j-1$列表示当前行已决策的下插头，第$j$列表示$(i,j-1)$已决策的右插头，$j+1$到最后一列分别表示上一行的下插头。

如图：红色格子是最近一排已决策的格子，蓝线是需要状压记录的插头状态。

状态转移

行间转移

设列数为$m$，状压需要记录的$m+1$个插头下标分别为$0-m$。

一行处理完之后，$0-(m-1)$位分别代表每个下插头，而转移到下一行第一个格子时，应当由$1-m$位来表示，所以整体右移一位即可。

行内转移

我们以最简单的模型：用任意条简单回路遍历整个棋盘的方案数。

注意到每个格子都处于回路上，所以必然连接两个的插头。我们只需要维护状态$0/1$，分别表示有无插头即可。

分类讨论如下：

• 左上均无插头，则右下均设立插头
• 只有左或上有插头，则将插头拐弯或直走，分别判断会不会走到边界情况后转移。
• 左上均有插头，合并两个插头，不再向右下设立插头。

在处理完所有格子后，所以状态为0的即可计入答案。

代码实现

往往因为某些题目的特殊要求，我们需要设置大于2种的插头，而种数有时并不是2的整次幂，种数进制下状态压缩中转码和压缩的效率很低，所以依旧以不小于种数的最小2的整次幂作为进制处理。

而在转移中，存在大量无用的不合法状态，这时就需要哈希表来存储所有合法状态。

struct Hs{
   int val[mod],key[mod],hs[mod],sz;
   inline void itia(){
      memset(val,0,sizeof(val));//根据题目要求初始化
      memset(key,0xff,sizeof(key));
      memset(hs,0,sizeof(hs));sz=0;
   }
   inline void nh(int u,int v){key[++sz]=v;hs[u]=sz;}
   int &operator [](const int S){
       for(int i=S%mod;;i=(i+1==mod)?0:(i+1)){
           if(!hs[i]) nh(i,S);
           if(key[hs[i]]==S) return val[hs[i]];
       }
   }
}f[2];

而转码通常以函数形式写出(设进制为4)：

inline int gt(int S,int pos){return ((S>>((pos-1)<<1))&3);}
inline void sett(int &S,int pos,int v)
{pos=(pos-1)<<1;S|=(3<

---

常见模型

常见的几种插头设置方式：

• 括号匹配
• 独立插头
• 最小表示法

---

1.bzoj1210: [HNOI2004]邮递员

求一遍遍历整个棋盘的简单回路的方案数。

相比用任意条简单回路遍历整个棋盘，这道题对于左上都有插头的情况多了一个限制：除非是右下角，否则两插头不能处于同一联通块。

于是我们可以用最小表示法来进行转移：用不同标号表示不同的联通既可。

但观察下面的图：

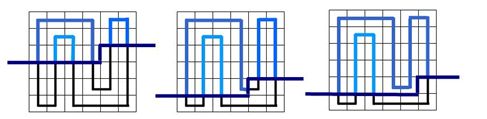
可以发现，轮廓线上方的路径是由若干条互不相交的路径构成了。而且每条路径在轮廓线上存在对应的两个插头。

于是可以用括号匹配表示插头。1,2分别表示左右插头。它们最近的相异插头就是对应的相同联通块的另一个插头。

#include
using namespace std;
const int N=(1<<20)+10,bs=1e9;
const int mod=2601;

int n,m,pr,pt=1;

struct bint{
    int bit[7];
    inline void clr(){memset(bit,0,sizeof(bit));}
    bint(){clr();}
    inline void sett(int x){for(clr();x;x/=bs)bit[++bit[0]]=x%bs;}
    void operator =(int x){sett(x);}
    int &operator [](int x){return bit[x];}
    bint operator +(bint ky){
        bint re;re.clr();int i,j;
        j=re[0]=max(bit[0],ky[0])+1;
        for(i=1;i<=j;++i){
        	re[i]+=bit[i]+ky[i];
        	re[i+1]+=re[i]/bs;re[i]%=bs;
        }
        for(;re[0]>0 && (!re[re[0]]);--re[0]);
        return re;
    }
    void operator +=(bint ky){*this=*this+ky;}
    inline void prit(){
    	printf("%d",bit[bit[0]]);
    	for(int i=bit[0]-1;i>0;--i) printf("%09d",bit[i]);
    }
}ans;

struct Hs{
    bint val[mod];int key[mod],hs[N],sz;
    inline void itia(){
        memset(val,0,sizeof(val));memset(key,0xff,sizeof(key));
        memset(hs,0,sizeof(hs));sz=0;
    }
    inline void nh(int u,int v){key[++sz]=v;hs[u]=sz;}
    bint &operator [](const int sta){
        for(int i=sta%mod;;i=(i+1==mod)?0:(i+1)){
            if(!hs[i]) nh(i,sta);
            if(key[hs[i]]==sta) return val[hs[i]];
        }
    }
}f[2];

inline int gt(int S,int pos){return ((S>>((pos-1)<<1))&3);}
inline void sett(int &S,int pos,int vl)
{pos=(pos-1)<<1;S|=(3<n) swap(n,m);
    if(m==1) {putchar('1');return 0;}
    f[0].itia();f[0][0]=1;
    for(i=1;i<=n;++i){
        for(j=1;j<=m;++j) cal(i,j);
        if(i==n) break;
        for(j=f[pr].sz;j;--j) f[pr].key[j]<<=2;
    }
    ans=ans+ans;ans.prit();
    return 0;
}

---

2.bzoj2310: ParkII

求一条简单路径，使得经过的点权值之和最大。

建2个独立插头（也就是没有对应左右插头），延伸即可。

#include
using namespace std;
const int mod=22787;

int g[102][10],n,m;
int ans,pr,pt=1;

struct Hs{
	int key[mod],sz,val[mod],hs[mod];
    inline void itia(){
    	memset(key,0xff,sizeof(key));memset(val,0x8f,sizeof(val));
    	sz=0;memset(hs,0,sizeof(hs));
    }
    inline int nh(int u,int v){key[++sz]=v;hs[u]=sz;}
    inline int &operator [](const int S){
    	for(int i=S%mod;;i=(i+1==mod)?0:(i+1)){
    		if(!hs[i]) nh(i,S);
    		if(key[hs[i]]==S) return val[hs[i]];
    	}
    }
}f[2];

inline int gt(int S,int pos){return ((S>>((pos-1)<<1))&3);}
inline void sett(int &S,int pos,int vl)
{pos=(pos-1)<<1;S|=(3<>=2){
		j=S&3;
		if(j==3) cnt++;
		else if(j==1) cot--;
		else if(j==2) cot++;
	}
	return ((cnt>2)||(cot!=0));
}

inline void upp(int &x,int y){x=(y>x)?y:x;}

inline void cal(int x,int y)
{
	pr^=1;pt^=1;f[pr].itia();
	int i,j,k,t,S,res,vl,a,b;
	for(i=f[pt].sz;i;--i){
		S=f[pt].key[i];vl=f[pt].val[i];
		a=gt(S,y);b=gt(S,y+1);
		if(ck(S)||(S>=(1<<((m+1)<<1)))) continue;
		vl+=g[x][y];
		if((!a)&&(!b)){
			upp(f[pr][S],vl-g[x][y]);
			if((x

---

3.bzoj2331: [SCOI2011]地板

求用L型的地板铺满整个客厅的方案数。

设$0,1,2$分别表示没有插头，没有拐过弯的插头，拐过弯的插头即可。

#include
using namespace std;
const int mod=20110520,bs=200097;

int n,m,pr,pt=1,ans,lsx,lsy;
char bn[105][105],rq[105];

inline void ad(int &x,int y){x+=y;if(x>=mod) x-=mod;}

struct Hs{
	int val[bs],sz,key[bs],hs[bs];
	inline void itia(){
		memset(val,0,sizeof(val));memset(key,0xff,sizeof(key));
		memset(hs,0,sizeof(hs));sz=0;
	}
	inline void nh(int u,int v){key[++sz]=v;hs[u]=sz;}
	int &operator [](const int S){
		for(int i=S%bs;;i=(i+1==bs)?0:(i+1)){
			if(!hs[i]) nh(i,S);
			if(key[hs[i]]==S) return val[hs[i]];
		}
	}
}f[2];

inline void init()
{
	int i,j;
	scanf("%d%d",&n,&m);
	if(m>n){
		for(i=1;i<=n;++i){
			scanf("%s",rq+1);
			for(j=1;j<=m;++j) 
			 bn[j][n+1-i]=rq[j];
		}
		swap(n,m);
	}else for(i=1;i<=n;++i) scanf("%s",bn[i]+1);
	for(i=1;i<=n;++i)
	 for(j=1;j<=m;++j){
	 	bn[i][j]=(bn[i][j]!='*');
	 	if(bn[i][j]) lsx=i,lsy=j;
	 }
	  
}

inline int gt(int S,int pos){return ((S>>((pos-1)<<1))&3);}
inline void sett(int &S,int pos,int v)
{pos=(pos-1)<<1;S|=(3<

4.bzoj2595: [Wc2008]游览计划

最小表示法维护联通块即可。
题解