使用Excel创建线性回归模型
作者|RAM DEWANI 编译|VK 来源|Analytics Vidhya
概述
你可以在Excel中执行建模,只需几个步骤
下面是一个教程,介绍如何在Excel中构建线性回归模型以及如何解释结果
介绍
Excel真的能构建预测模型?
这通常是我提起这个话题时的第一反应。当我演示如何利用Excel的灵活性为我们的数据科学和分析项目构建预测模型时,接下来是一个令人怀疑的眼神。
让我问你一个问题-如果你周围的商店开始收集客户数据,他们是否可以采用基于数据的策略来销售他们的商品?他们能预测自己的销售额或估计可能销售的产品数量吗?
现在你一定想知道,他们究竟将如何建立一个复杂的统计模型来预测这些事情?学习分析或雇佣分析师可能超出了他们的能力范围。好消息是,他们不需要。
Microsoft Excel为我们提供了一种构建预测模型的能力,而不必编写复杂的代码。
我们可以很容易地在MS Excel中建立一个简单的线性回归模型,它可以帮助我们在几个简单的步骤中执行分析。我们不需要精通Excel或统计学就可以进行预测建模!
在这篇文章中,我将解释如何在Excel中建立一个线性回归模型,以及如何对结果进行分析,以便你成为一名分析师!
目录
什么是线性回归?
在Excel中获取所有重要的Add分析工具包
在Excel中实现线性回归
解释我们预测模型的结果
我们如何改进模型?
用Excel做预测!
什么是线性回归?
线性回归是我们大多数人学习的第一种机器学习技术。它也是业界最常用的监督学习技术。
但什么是线性回归?
它是一种线性方法,用于统计建模因变量(要预测的变量)和自变量(用于预测的因素)之间的关系。线性回归给出了这样一个方程:
这里,Y是因变量,X是自变量,C是系数。系数基本上是根据重要性分配给特征的权重。
最常用的回归方法是OLS(普通最小二乘法)。它的目标是减少平方和以产生这样的最佳拟合线:
如果你想了解有关线性回归的更多信息,请参阅以下资源:
线性回归基础:https://courses.analyticsvidhya.com/courses/Fundamentals-of-Regression-Analysis
线性回归模型中的诊断图:https://www.analyticsvidhya.com/blog/2013/12/residual-plots-regression-model/
Excel中线性回归的初学者指南:https://www.analyticsvidhya.com/blog/2017/06/a-comprehensive-guide-for-linear-ridge-and-lasso-regression/
Excel加载项获取分析工具包
要在Excel中执行回归分析,首先需要启用Excel的分析工具包加载项。Excel中的分析工具包是一个插件程序,为统计和工程分析提供数据分析工具。
要将其添加到工作簿中,请执行以下步骤。
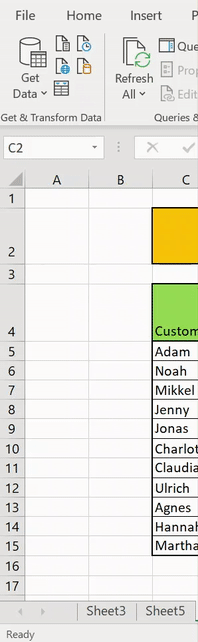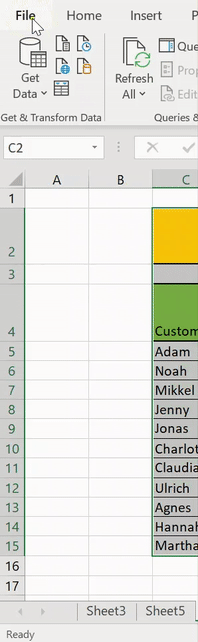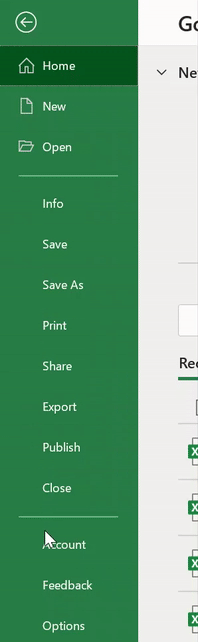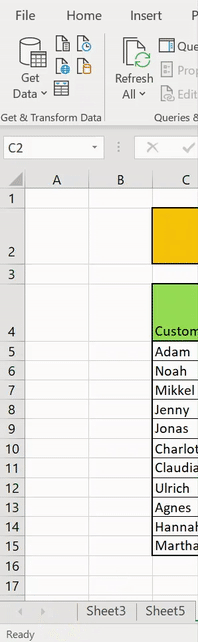
步骤1–Excel选项
转到文件->选项:
步骤2–定位分析工具包
转到左侧面板上的加载项->管理Excel加载项->转到:
第3步-添加分析工具包
选择“分析工具包”并按“确定”:
你已在Excel中成功添加分析工具包!你可以通过转到功能区中的数据栏进行检查。
让我们开始用Excel建立我们的预测模型!
在Excel中实现线性回归
到目前为止,很多东西都是理论上的。现在,让我们深入了解Excel并进行线性回归分析!
下面是我们将要处理的问题声明:
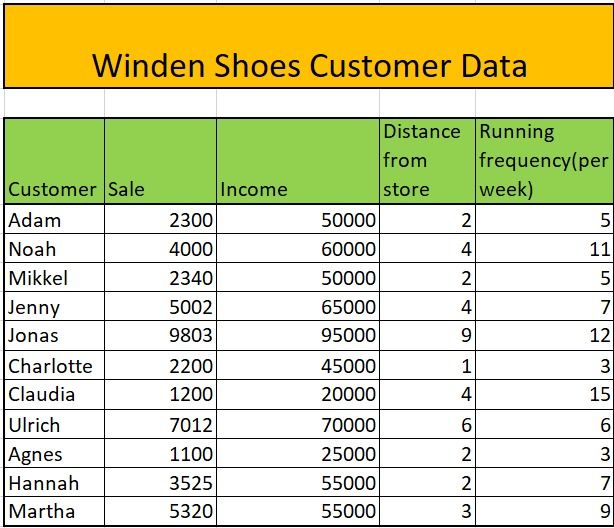
Winden镇有一家卖鞋的公司。该公司希望通过考虑以下因素来预测每个客户的销售情况:客户收入、离家距离、客户每周的跑步频率。
步骤1–选择回归
进入数据->数据分析:
转到数据工具包中的“数据分析”,选择“回归”,然后按“确定”:
步骤2–选择
在这一步中,我们将选择一些分析所需的选项,例如:
输入y范围–独立因子的范围
输入x范围-相关因素的范围
输出范围–要显示结果的单元格范围
其他选项是自由选择的,你可以根据你的特定目的选择它们。
按OK,我们最终在Excel中用两个步骤进行了回归分析!很简单!现在我们将在excel中看到回归分析的结果。
用Excel分析预测模型的结果
实施线性回归模型是最简单的部分。现在是我们分析的棘手方面——在Excel中解释预测模型的结果。
综上所述,我们有三种产出类型,我们将逐一介绍:
回归统计表
方差分析表
回归系数表
残差表
回归统计表
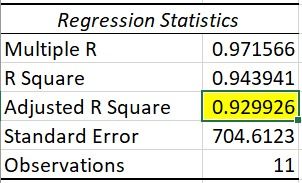
回归统计表告诉我们最佳拟合线如何定义自变量和因变量之间的线性关系。两个最重要的度量是R方和调整R方。
R方统计量是拟合优度的指标,它告诉我们最佳拟合线解释了多少方差。R方的范围从0到1。
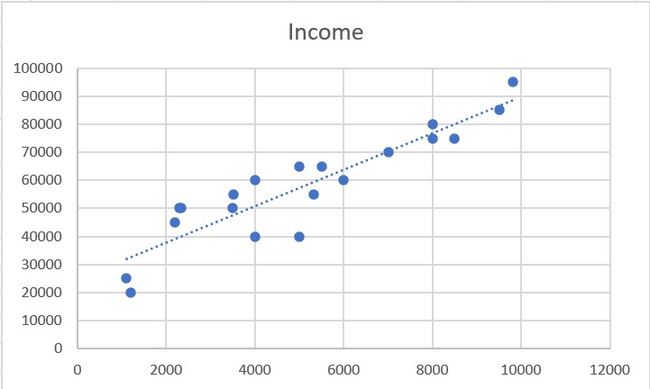
在我们的例子中,R平方值为0.953,这意味着我们的行能够解释95%的方差——这是一个好的迹象。
但是有一个问题-当我们不断增加更多的变量,我们的R平方值将继续增加,即使变量可能没有任何影响。调整R平方解决了这个问题,是一个更可靠的度量。
方差分析表
方差分析代表方差分析。此表将平方和分解为其组成部分,以提供模型内变化的详细信息。
它包括一个非常重要的指标,显著性F(或P值),它告诉我们你的模型是否具有统计显著性。
简而言之,这意味着我们的结果可能不是由于随机性,而是因为一个潜在的原因。
p值最常用的阈值是0.05。如果我们得到的值低于这个,就可以了。否则,我们需要选择另一组自变量。
在我们的例子中,我们的值远低于0.05的阈值。太棒了,我们现在可以前进了!
回归系数表
系数表以系数的形式分解回归线的组成部分。从中我们可以了解很多。
对于Winden鞋业公司来说,似乎每增加一个单位的收入,销售额就增加0.08,而增加一个单位的店面距离就增加508个销售额!
running frequency的增加似乎使销售量减少了24,但我们真的能相信这个特征吗?
如果你看上面的图片,你会发现它的p值大于0.5,这意味着它在统计学上不显著。
我们将在下一节探讨如何处理这种情况。
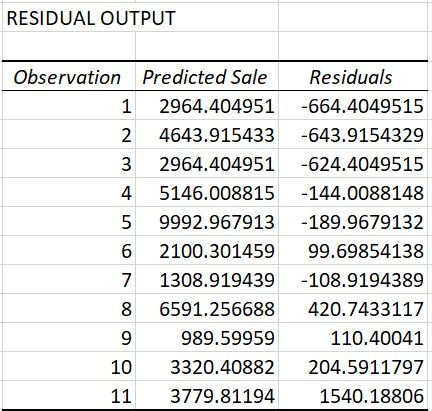
残差表
残差表反映了预测值与实际值之间的差异。它由我们的模型预测的值组成:
如何改进我们的模型?
如前所述,变量running frequency的p值大于0.05,因此让我们从分析中移除该变量来检查结果。
我们将遵循上述所有步骤,但不包括running frequency列:
我们注意到调整后的R平方的值从0.920略微提高到0.929!
用Excel做预测!
我们已经准备好回归分析了,现在该怎么办?让我们看看。
你的一位老顾客,名叫亚历山德,走进来,我们想预测他的销售额。我们可以简单地从线性回归模型的数据中插入数字,我们很好去!
Aleksander有4万的收入,住在离商店2公里的地方。估计销售额是多少?
方程变成:
在这里,我们的模型估计,亚历山德先生将支付4218购买他的新鞋!这就是简单地在Microsoft Excel中进行线性回归的能力。
结尾
在本文中,我们学习了如何在Excel中建立线性回归模型以及如何解释结果。我希望这本教程能帮助你成为一个更好的分析师或数据科学家。
分析工具包包含许多其他Excel分析选项。你可以在日常生活中尝试很多其他的统计分析!
原文链接:https://www.analyticsvidhya.com/blog/2020/06/predictive-modeling-excel-linear-regression/
欢迎关注磐创AI博客站: http://panchuang.net/
sklearn机器学习中文官方文档: http://sklearn123.com/
欢迎关注磐创博客资源汇总站: http://docs.panchuang.net/