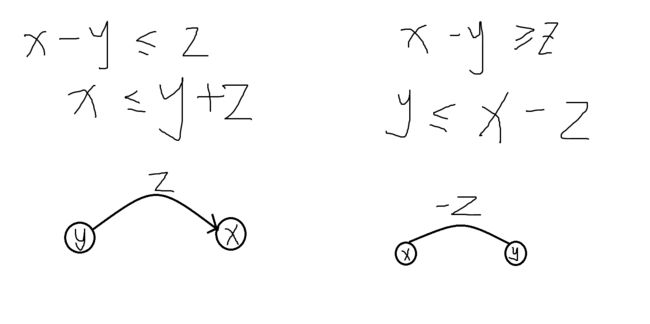差分约束系统是个啥呢?可能看名字非常地难理解,其实它要求的就是一个n元一次不等式组的解,形式如下:
\(\begin{cases}x-y \leq 10\\y-z \leq 5\\\end{cases}\)
那么求解这一组数据的解,就是差分约束系统的目的
那么对于以上这一个用数学方式来求解的不等数组,我们如何用一个程序来实现呢?我们将以上式子做一个移项的处理得到:
\(\begin{cases}x\leq y+10\\y\leq z+5\\\end{cases}\)
仔细观察以上式子,然后再来观察一下最短路中的松弛操作
\(d[y] \leq d[x]+z\)
当所有的\(x\)和\(y\)满足以上式子之后,我们就求出了最短路,再对比上面的不等式组,不难发现他们有相似之处,我们就可以将不等式组的每一个式子进行移项得到一个类似松弛操作的式子,然后转化为最短路求解
对于小于等于的情况跑最短路,当然也会出现大于等于的情况,这个时候我们应该跑最长路。但是我学习的时候,看了很多博客都只是写了这个结论的东西,如果你无法分清楚这一种情况,我们可以结合数学的知识来理解,如下:
\(\begin{cases}x\leq10\\x\leq5\\\end{cases}\) 和 \(\begin{cases}y\geq10\\y\geq5\\\end{cases}\)
我们得出的答案应该是 \(x \leq 5\) 和 \(y \geq10\) (初中数学基本知识),我们应该的正解应该是范围更小的那一个。对于小于等于,最短路会使得答案范围更小;相反,大于等于的话,最长路使得答案范围更小,满足不等式组的求解
然后就是对于不同符号的转换:
如果是 \(x-y=z\) ,我们可以转化为 \(x-y\geq z\)且\(x-y \leq z\)
如果是 \(x-y \geq z\) ,我们可以转化为 \(y \leq x-z\)
如果是 \(x-y \leq z\) ,我们可以转化为 \(y \geq x-z\)
不难发现大于等于和小于等于的情况其实是可以互相转换的,但是在你做题的时候你会发现,转化之后求最长路或是最短路和转化之前求解的答案不相同,是因为你的最短路的\(d[ ]\)的初始值的原因,这样求出来的解是符合该不等式组的,但是我们人为的会对初始值进行赋值,才会导致答案不同,因为不等式组的解是无数的
讲解了如何转换一类的基础知识,我们就要开始落实程序了,就是关于如何将不等式组转化为图然后跑最短(长)路的问题,以及判断无解的情况
对于建图(这里只会讲解用链式前向星),就像图示一样建图就可以了(都是有向边,第二张图有点问题),不理解的建议自己手推一下:
但是如何判断无解的情况呢?其实就是判断有环的情况:
\(\begin{cases}x \leq y\\y \leq z \\ z \leq x\\\end{cases}\)
这一个不等式组建图之后就会出现环的情况,我们只需要再最短路中判断是否有环的情况就可以了
知道以上的东西之后,我们就可以确定最短路的算法了,又有负边权,又有判断环,那么可以选择就是Ford算法和SPFA算法,至于用哪一个算法,我个人推荐SPFA,毕竟大部分时候会快一点
那么对于差分约束系统的核心思想就讲到这里了,我们通过一些例题来加深理解和落实代码就可以了
P3385 【模板】负环
从基础的开始,先做判断负环的情况,我这里就直接贴代码了,不知道在最短路中如何判断环的情况的可以直接看代码,如果对最短路不太熟悉的可以参考我的另一篇博客
#include
using namespace std;
const int MAXN=9*1e5+51;
int T;
int n,m;
struct node{
int net,to,w;
}e[MAXN];
int head[MAXN],tot;
void add(int x,int y,int z){
e[++tot].net=head[x];
e[tot].to=y;
e[tot].w=z;
head[x]=tot;
} //链式前向星
int d[MAXN]; //记录距离
bool v[MAXN]; //是否入队
int cnt[MAXN]; //入队次数
bool spfa(int s){
queueq;
for(register int i=1;i<=n;i++){
d[i]=20050206,v[i]=false,cnt[i]=0;
}//初始化
d[s]=0;
cnt[s]=1;
v[s]=true;
q.push(s);
while(!q.empty()){
int x=q.front();
q.pop();
v[x]=false;
for(register int i=head[x];i;i=e[i].net){
int y=e[i].to,z=e[i].w;
if(d[y]>d[x]+z){
d[y]=d[x]+z;
cnt[y]++; //入队次数++
if(cnt[y]>=n) return false; //如果入队次数超过n,说明有负环
if(v[y]==false){
v[y]=true;
q.push(y);//入队
}
}
}
}
return true; //记得return true,默认的是return false
}
int main(){
scanf("%d",&T);
while(T--){
memset(head,0,sizeof head);
tot=0; //记得每一次初始化
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
if(z>=0) add(y,x,z); //按照题目来建边
}
if(spfa(1)==false) puts("YES");
else puts("NO");
}
return 0;
}
P5960 【模板】差分约束算法
#include
using namespace std;
const int MAXN=2*1e5+51;
int n,m;
struct node{
int net,to,w;
}e[MAXN];
int head[MAXN],tot;
void add(int x,int y,int z){
e[++tot].net=head[x];
e[tot].to=y;
e[tot].w=z;
head[x]=tot;
}
int d[MAXN],vis[MAXN];
bool v[MAXN];
bool spfa(int s){
queueq;
for(register int i=1;i<=n;i++){
d[i]=20040915,v[i]=false,vis[i]=0;
}
v[s]=true;
d[s]=0;
vis[s]=1;
q.push(s);
while(!q.empty()){
int x=q.front();
q.pop();
v[x]=false;
for(register int i=head[x];i;i=e[i].net){
int y=e[i].to,z=e[i].w;
if(d[y]>d[x]+z){
d[y]=d[x]+z;
vis[y]++;
if(vis[y]>=n) return false;
if(v[y]==false){
q.push(y);
v[y]=true;
}
}
}
}
return true;
}
int main(){
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(y,x,z);
}
for(register int i=1;i<=n;i++){
add(0,i,0);
} //因为你不知道哪一个点是起点,我们建立一个超级源点来遍历所有点
if(spfa(0)==true){
for(register int i=1;i<=n;i++){
cout<
做完模板题之后,我会给出几道我自己认为还不错的可以加深理解的题,也会给出一些解题方法和注意要点
P4878 [USACO05DEC]Layout G
为什么会推荐这道题呢?因为这道题初看其实就是一道很纯的模板题,没有任何区别,只是将大于等于和小于等于转化一下就可以了,但是对于后三组数据你并不能过,因为它有一些特殊的情况
题目中表面说了,求1到N的答案,所以很多人就会直接从1开始跑最短路,然而这是错误的,因为我们没有判断图并不是连通的,什么意思,就是1这个点是孤儿点或者1根本不可能走向n,这个时候我们就需要建立一个超级源点来做了
#include
using namespace std;
const int MAXN=1e5+10;
const int INF=2004091500;
int n,l,D;
struct node{
int net,to,w;
}e[MAXN];
int head[MAXN],tot;
void add(int x,int y,int z){
e[++tot].net=head[x];
e[tot].to=y;
e[tot].w=z;
head[x]=tot;
}
int d[MAXN],vis[MAXN];
bool v[MAXN];
bool spfa(int s){
queueq;
for(register int i=1;i<=n;i++){
d[i]=INF,vis[i]=0,v[i]=false;
}
d[s]=0;
vis[s]=1;
v[s]=true;
q.push(s);
while(!q.empty()){
int x=q.front();
q.pop();
v[x]=false;
for(register int i=head[x];i;i=e[i].net){
int y=e[i].to,z=e[i].w;
if(d[y]>d[x]+z){
d[y]=d[x]+z;
vis[y]++;
if(vis[y]>=n) return false;
if(v[y]==false){
v[y]=true;
q.push(y);
}
}
}
}
return true;
}
int main(){
scanf("%d%d%d",&n,&l,&D);
for(register int i=1;i<=n;i++) add(0,i,0); //建立超级源点
for(register int i=1;i<=l;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
}
for(register int i=1;i<=D;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(y,x,-z);
} //分清楚两种建边的情况
if(spfa(0)==false) puts("-1"); //先跑0判断是否连通
else if(spfa(1)==false) puts("-1"); //再跑1看是否负环
else{
if(d[n]==INF) puts("-2"); //是否不连通
else printf("%d",d[n]);
}
return 0;
}
P3275 [SCOI2011]糖果
给这道题的原因就是对于给你一个题目,判断到底应该跑最长路还是最短路,用小于等于还是大于等于,很明显,求至少跑多少,是大于等于,跑最长路
然后就是对于不同情况应该如何建边
#include
using namespace std;
queue q;
long long n,m,tot;
long long ans;
long long dis[2000050],cnt[2000050],head[2000050];
bool vis[2000050];
struct node {
long long to,net,val;
} e[2000050];
void add(long long u,long long v,long long w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
bool spfa(int s) {
vis[s]=true;
cnt[s]=1;
q.push(s);
while(!q.empty()) {
long long x=q.front();
q.pop();
vis[x]=false;
for(register long long i=head[x];i;i=e[i].net) {
long long v=e[i].to;
if(dis[v]=n) return false;
if(vis[v]==false) {
vis[v]=true;
q.push(v);
}
}
}
}
return true;
}
int main() {
scanf("%lld%lld",&n,&m);
for(register long long i=1;i<=m;i++) {
long long x,u,v;
scanf("%lld%lld%lld",&x,&u,&v);
if(u==v&&x%2==0){
puts("-1");
return 0;
}
if(x==1) {
add(u,v,0);
add(v,u,0);
}
else if(x==2) add(u,v,1);
else if(x==3) add(v,u,0);
else if(x==4) add(v,u,1);
else add(u,v,0);
}
for(register long long i=1;i<=n;i++) add(0,i,1);
if(spfa(0)==false) puts("-1");
else {
for(register long long i=1;i<=n;i++) {
ans+=(dis[i]);
}
printf("%lld",ans);
}
return 0;
}
然后你会发现你自己超时了,之后我会将如何优化这个程序,先放在这里
P2294 [HNOI2005]狡猾的商人
这道题要仔细讲一讲,因为我们之后做的题肯定不是像上面一样的纯模板题,是需要一些转换的。就拿这道题来说,我最开始没想出什么思路,打了一个错误的暴力11分,看着旁边的大佬直接用所谓的“暴力”A了这道题,我还是选择看题解,因为实在是太菜啊
因为这道题,它的题目意思是 这几个月一共的收入 ,那么我们就可以想到前缀和 ,例如\((1,3,5)\) 表示1到3月份的收入是5块钱,就可以转化为\(sum[3]-sum[1-1]=5\) 的方式(前缀和的基本操作),那么对于一组数据\((u,v,w)\),就可以以\(u-1\)和\(v\)为两个端点,\(w\)就为边权,连两条边,因为是等于的情况,那么直接看程序
#include
using namespace std;
int T,n,m,u,v,w,tot;
int dis[250010],cnt[250010],head[250010];
bool vis[250010];
struct node {
int to,net,val;
} e[250010];
inline void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
inline bool spfa() {
queue q;
for(register int i=0;i<=n;i++) {
cnt[i]=0;
vis[i]=true;
q.push(i);
}
//这个地方可以仔细说一下,我前面几个程序在不确定起始点的情况下,都是用的超级源点
//其实也可以直接全部入队,达到的目的是一样的
//但是貌似全部入队会快一点,上面那道糖果用全部入队的方式就可以直接A
while(!q.empty()) {
int x=q.front();
q.pop();
vis[x]=false;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(dis[v]>dis[x]+e[i].val) {
dis[v]=dis[x]+e[i].val;
cnt[v]++;
if(cnt[v]>=n) return false;
if(vis[v]==false) {
vis[v]=true;
q.push(v);
}
}
}
}
return true;
}
int main() {
scanf("%d",&T);
while(T--) {
tot=0;
memset(head,0,sizeof head);
memset(vis,false,sizeof vis);
memset(cnt,0,sizeof cnt);
memset(dis,0,sizeof dis);//清空数组
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++) {
scanf("%d%d%d",&u,&v,&w);
add(u-1,v,-w); //转化为前缀和的形式,本题核心
add(v,u-1,w); //等于的情况建两条边
}
if(spfa()==false) puts("false");
else puts("true");
}
return 0;
}
那么题就讲完了,剩下的就靠自己刷题领悟和加深理解了,在最后,我还是想讲一讲关于SPFA的简单优化,只会涉及一点,其他的优化可以去参照一下其他dalao的博客
SLF优化,就是将队列改为双端队列,在插入队列的时候判断插入位置,起到一个很好的优化
dequeq
while(!q.empty()) {
int x=q.front();
q.pop_front();
vis[x]=false;
for(register int i=head[x]; i; i=e[i].net) {
int v=e[i].to;
if(dis[v]>dis[x]+e[i].val) {
dis[v]=dis[x]+e[i].val;
cnt[v]++;
if(cnt[v]>=n) return false;
if(vis[v]==false) {
vis[v]=true;
if(!q.empty()&&d[q.front()]
感谢一下ZJY dalao,同桌和RHL dalao在学习时提供给我的帮助
本篇博客就讲到这里了,如果有任何错误请在评论区指出,谢谢阅读