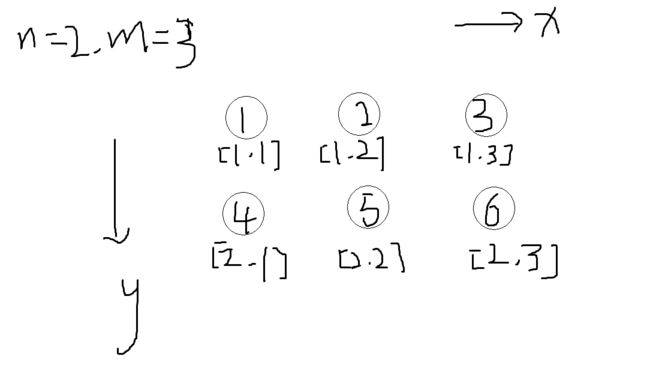小明的游戏就是玩棋盘???和这道题有啥区别啊。。如果不加多组测试数据,这道题可能还没那道题难。好了,吐槽结束
首先还是按照比较常规的思路来想,上下左右都已经写出来了,DFS和BFS没得跑,蒟蒻不太会处理BFS,因为实在没有想出来怎么写,所以第一次我写的是DFS+记忆化搜索,水了60分,因为DFS本来就慢,还有多组数据,剩下两个点超时,所以应该换一种思路
#include
using namespace std;
int n,m;
char aa[10005];
int a[1005][1005];
int mx[4]= {0,-1,1,0};
int my[4]= {1,0,0,-1}; //上下左右移动
int f[1005][1005]; //记忆化搜索
int bx,by,ex,ey; //起点终点
bool v[1005][1005]; //是否走过
inline void dfs(int x,int y,int sum) {
if(sum>f[x][y]) return ; //如果答案比目前最优答案大,return
for(register int i=0; i<4; i++) {
int nx=x+mx[i];
int ny=y+my[i];
if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&v[nx][ny]==false) { //不越界,可以走
if(a[nx][ny]==a[x][y]&&sum>aa+1;
for(register int j=1; j<=m; j++) {
if(aa[j]=='@') a[i][j]=1;
else a[i][j]=2;
}
}//建造一个初始的矩阵
scanf("%d%d%d%d",&bx,&by,&ex,&ey);
bx++,by++,ex++,ey++;//从1开始处理更加方便
v[bx][by]=true;
dfs(bx,by,0); //搜索
printf("%d\n",f[ex][ey]);
}
return 0;
}
我选择打开了算法标签->最短路。但是我们学过的最短路都是在很多点直接跑,而这是一个矩阵,不好处理,所以我们可以想办法把这一个矩阵拉成一条链或是平时我们学过的图形结构处理
其实我们可以画一个图来理解这个东西,其实还是很简单的,我这里把公式也写出来,\(id=(x-1)*m+y\),当然如果你想写成一些类似的算式那当然也可以
把点处理之后我们就要开始考虑边权的问题了,对于一个点,我们还是对周围的上下左右四个点进行建边,而对于异或,它是很美妙的,相同为1,不同为0,所以这道题刚好就可以利用这个性质建边,就可以了,那么剩下的就是常规跑最短路
但是这里感觉是有一个坑的,我自己没想出来为什么,我最开始用Dijkstra写的,这里也不会有负边的情况,但是跑炸了,可能是一些细节错误,然后我就改成SPFA了
#include
using namespace std;
const int MAXN=20000005;
int n,m;
struct node {
int net,to,w;
} e[MAXN];
int head[250005],tot;
void add(int x,int y,int z) {
e[++tot].net=head[x];
e[tot].to=y;
e[tot].w=z;
head[x]=tot;
}//链式前向星建边
int d[250005]; //最短路答案
bool v[250005]; //是否入队
int a[505][505]; //用来存储图
char aa[505]; //输入
int bx,by,ex,ey; //起点,终点
void spfa(int s) {
queueq;
for(register int i=1; i<=n*m+1; i++) {
d[i]=2000040915,v[i]=false;
}
d[s]=0;
v[s]=true;
q.push(s);
while(!q.empty()) {
int x=q.front();
q.pop();
v[x]=false;
for(register int i=head[x]; i; i=e[i].net) {
int y=e[i].to,z=e[i].w;
if(d[y]>d[x]+z) {
d[y]=d[x]+z;
if(v[y]==false){
q.push(y);
v[y]=true;
}
}
}
}
}//正常的SPFA
int main() {
while(1) {
scanf("%d%d",&n,&m);
if(n==0&&m==0) return 0;
memset(head,0,sizeof head);
tot=0;//初始化
for(register int i=1; i<=n; i++) {
cin>>aa+1;
for(register int j=1; j<=m; j++) {
if(aa[j]=='@') a[i][j]=1;
else a[i][j]=0;//这里写成0和1是为了符合以上说的异或的性质
}
}
for(register int i=1; i<=n; i++) {
for(register int j=1; j<=m; j++) {
if(i>1) add((i-1)*m+j,(i-2)*m+j,a[i][j]^a[i-1][j]),add((i-2)*m+j,(i-1)*m+j,a[i][j]^a[i-1][j]);
if(i1) add((i-1)*m+j,(i-1)*m+j-1,a[i][j]^a[i][j-1]),add((i-1)*m+j-1,(i-1)*m+j,a[i][j]^a[i][j-1]);
if(j