IGCV1(Interleaved Group Convolutions for Deep Neural Networks)论文解读

原文链接：https://arxiv.org/abs/1707.02725
作者视频讲解链接：https://edu.csdn.net/course/play/8320/171433?s=1

Abstract

在本篇论文中，我们提出了一种简单的模块化网络结构，将其称为交错组卷积神经网络(IGCNets)。它的重点在于一个新颖的构建块：是由一对连续且相互交错的组卷积组成。这两个组卷积是互补的：

1. 在第一个组卷积中的卷积都是空间域卷积；第二个组卷积中的卷积是逐点卷积；
2. 第二个组卷积中同一个分组内的所有通道来自于第一个组卷积中不同分组；

我们讨论了这样做的一个代表性优势：比起普通卷积，我们在网络参数量和计算复杂度不变的同时，使得网络变得更宽了。

1. Introduction

论文的关注点在于减少卷积核的冗余，这种冗余来自于两个方面：空间方面和通道方面。在空间方面，小的卷积核例如3x3、1x3、3x1等尺寸已经开始被利用；在通道方面，组卷积和深度分离卷积也已经被研究。我们的工作属于在通道方面的卷积核设计。

在这篇论文中，我们展示了一种新颖的网络结构，它是一种交错组卷积块的堆叠结构。每个块包含两个组卷积：第一次组卷积核第二次组卷积，所谓组卷积就是在卷积时有两个分组。第一次组卷积是把输入通道划分为L个组，每个组包含M个通道，然后将L个分组卷积的结果拼接在一起得到新的输入其仍然有L*M个通道之后打乱顺序；第二次组卷积划分了M个组，每个组包含L个通道，且这L个通道来自第一次分组卷积时的不同组。同时第一次卷积做的是空间域卷积，第二次做的是逐点卷积。Figure 1展示了IGC块：

众所周知，组卷积和使用稀疏卷积核的常规卷积操作是等价的：在不同分组内的通道没有连接关系。通常来讲，一个IGC块等价于两个稀疏矩阵做普通卷积操作产生一个密集核。我们展示了在相同数量的参数和计算复杂度下，IGC块要比空间卷积更宽。根据实验结果来讲，我们观察到在相同的参数量和计算复杂度下，使用IGC块堆叠的网络要比常规卷积的网络效果更好。

我们研究了与已经存在的相关模块之间的联系：

• 普通卷积和带有通道融合的组卷积都是交错组卷积，只是卷积核不同而已；
• IGC块的一种极限情况就是第二个组卷积只有一个分组，这和Xception非常接近；

我们的主要贡献在于：

• 我们展现了一种新颖的构建块——交错组卷积，它在参数和计算方面效率很高；
• 我们展示了在同等网络尺寸和计算复杂度下，我们提出的构建快要比常规组卷积块更宽，同时展现了优越的性能；
• 我们讨论了和常规卷积、Xception块、带有求和融合的组卷积之间的联系，说明了它们都是交错组卷积的特例；

2. Related Work

组卷积和多分支

组卷积第一次是应用在AlexNet中，是为了同时在两块GPU上训练网络解决了内存问题。channel-wise卷积是组卷积的一种极端情况，每个组只包含一个通道。

多分枝结构可以被视为组卷积的一种扩展，在每个分组进行卷积转换，不同的卷积层在不同的分组，例如Iception、deep-fused nets等。求和、平均和在卷积之后拼接经常用来混合输出。我们的方法进一步提高了参数效率，采用了第一次组卷积和第二次组卷积，在这里第二次组卷积扮演的角色就是将第一次组卷积的输出通道混合。

稀疏卷积核

稀疏卷积核已经被嵌入到卷积神经网络：卷积核经常有有限的空间范围。低秩卷积核学习小型卷积核，进一步稀疏化了连接。channel-wise随机稀疏连接是在通道范围内稀疏化了卷积核，每一个输出通道都只和输入通道的一个小子集连接。

我们的方法也是在通道范围内稀疏化卷积核，不同的是，我们在第一次组卷积中使用了结构化的稀疏连接——输入和输出的卷积通道被划分为不同的组，每一个输出组都只和同一组的输入通道有关。另外，我们使用了第二次组卷积——另一个结构化稀疏矩阵，这样的好处在于喂进第一次组卷积中输入的每一个通道和第二次组卷积输出的每一个通道之间有且只有一条路径存在(严格的互补条件导致等价权重核是密集的)。Xception，已经被展示了比Icption更有效率，并且它更接近我们的方法，我们展示了它是我们的IGC块的特殊情况。

分解

对每个层的卷积核做张量分解可以减少神经网络的冗余，加速训练。张量分解是指在空间维度、输入输出的通道维度上进行分解，寻找低秩张量对原来的张量进行近似。我们的方法并不是对已经训练好的网络的卷积核使用稀疏核的乘积进行近似，而是从头开始训练我们的网络，并且展现了网络可以提高参数效率和分类精度。

3. Our network

3.1 交错组卷积

定义

我们的构建块是基于组卷积的，将输入通道划分为几个组，在每一个分组内做常规卷积。组卷积可以看作是稀疏对角块卷积核的常规卷积，它的每个块(即每个分组)只对应一部分输入通道，并且不同分组之间没有连接关系。

交错组卷积由两个组卷积组成——第一次组卷积和第二次组卷积。一个例子就是如上面的Figure 1所示，我们使用第一次组卷积来处理空间关系（经常采用的是空间卷积核，如3x3）；第二次组卷积用来对第一次组卷积输出的通道进行混合（经常采用的是1x1的卷积核）.

第一次组卷积

先来定义一组符号：

• L：第一次组卷积中分组的数量（也是第二次组卷积中每个分组内包含的通道数）；
• M：第一次组卷积中每个分组内包含的通道数（也是第二次组卷积中的分组数量）；

我们可以下面的公式来表达第一次组卷积完成的操作：

第二次组卷积

我们的方法是将第一次组卷积的输出通道进行混合，{y1, y2, … , yL }划分为M个组，其中每个组有L个通道，第二次组卷积中同一个分组内的通道来自第一次组卷积中的不同组。我们采用了一种简单的方案来完成这个“混合”操作：第二次组卷积的第m个分组是由第一次组卷积中每组的第m个通道组成的，

第二次组卷积是在M个分组上完成的：


这反映了一个IGC块等价于两个稀疏卷积核乘积得到的卷积核做常规卷积操作。

3.2 分析

比常规卷积更宽

回忆一下前面介绍的一些符号，第一次组卷积的卷积核尺寸为S(对于 3x3 的卷积核来说 S = 9)，第二次组卷积的卷积核尺寸为 1(采用的是 1x1 的卷积核)。考虑一个空间位置，一个IGC块中参数的数量和计算复杂度其实是相同的，为：

这里就将 G = ML 定义为一个IGC块的宽度（通道数目）。

对于一个卷积核尺寸为S的常规卷积来说，输入输出宽度为C，那么参数数量可以表示为：

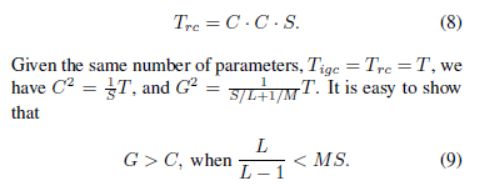
典型的S = 3x3 = 9，根据上面的分析，当 L>1时我们有 G>C。换句话说，一个IGC块要比常规卷积的宽度要宽，除了极端情况下第一次组卷积只有一个分组（L=1时）。

什么时候是最宽的？

我们讨论了第一次和第二次组卷积的分组数L和M是如何影响宽度的，考虑上面的等式7，我们有：

上面的不等式说明在给定参数量的情况下，宽度G是由上界的，当且仅当L=MS时G取得最大值。下面的table1中有两个例子，我们可以看到，当L=9M(S=9)时宽度是最大的：(i)中参数量大约为4672的情况下 3x9 大约等于27；(ii)中参数量大约为17536的情况下 5x9 大约等于41.

更宽就会导致更好的表现吗？

我们已经说明了一个IGC块和单独的常规卷积是等价的，这个常规卷积的卷积核是由两个稀疏核乘积得到的：

固定参数量意味着遵循下面的约束：

IGC块更宽就意味着输入的通道数增加了，Wp和Wd更大的同时也变得更加稀疏了。换句话来讲，组合的卷积核W变大的同时限制也更多了，导致的结果就是增加的宽度可能没有被完全探索导致表现不会提高。我们的实验结果如下图Figue 3 所示，验证了上面的观点并且给出了一个建议——选取接近最大宽度的IGC块，举个例子，在下图Figure 3中的两个例子，M=2实现了最好的表现。

4. Discussion and Connection

我们展示了常规卷积、组卷积之后做通道融合和Xception块都是IGC块的特例，并且了分别进行了讨论。

Connection to regular convolutions

在一个空间位置上的常规卷积可以写成 x’ = Wx(这里的x表示输入，W表示卷积核相关的权重矩阵，x’是输出)。如图Figure2所示，我们展示了常规卷积所对应的IGC块形式，这里是将L设置为4：

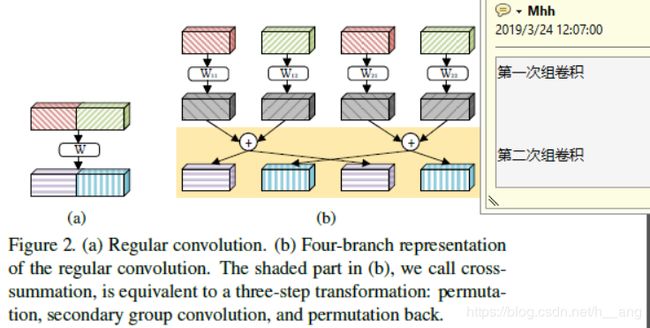
这里将看成100维的向量，W为100x100的矩阵，常规卷积就是进行Wx的运算，可以将输入分为两个50维度，W分成 2x2 的块；这时的运算和Figure 2(b)中的运算是等价的，即用一个IGC块对常规卷积进行等价，第一次组卷积是分别用W11、W12、W21和W22与输入的一部分做运算，第二次组卷积中每组的组卷积核都是相同的。

Connection to summation fusion

求和融合块是由多组分支组成，L个卷积块之后跟着一个求和操作，可以写成下面的形式：

其中x’是下一个组卷积层的输入，不像Figure 2(b)中的常规卷积，求和融合接受所有的四个输入，并将它们累加作为四个相同输出。在交错组卷积的形式中，第二个组卷积非常简单，并且每个分组卷积的卷积核都是相同的，举个例子，四个分组时对应的权重矩阵为：

Xception is an extreme case

我们讨论两种极端情况：L=1和M=1。当L=1时，第一次组卷积变成了常规卷积，第二次组卷积就是深度卷积；当M=1时，第一次组卷积局势一种极端情况下的组卷积：channel-wise组卷积，每个组内都只有一个通道，第二次组卷积是一个 1x1 的常规卷积，进行通道融合，这种极端情况和Xception块很相似，在Section 3.2中我们展示了这两种极端情况都没有导致最大的宽度，除非在同时满足 L=9 和 M=1时，我们Figure 3中的结果表明在L=1时网络表现很差，同时M=1时网络的表现也不是最好的。

Extensions and variants

首先，第一次组卷积和第二次组卷积中的卷积核是可以互换的：第一次组卷积使用 1x1 的卷积核，第二次组卷积使用空间卷积核(如尺寸为 3x3 的卷积核)，实验结果显示没有区别；第二点，第二次组卷积可以使用线性变化来替代，或者 1x1的常规卷积，其同样可以对第一次组卷积的输出通道信息进行混合；第二次组卷积也可以采用空间卷积。但我们并没有选择上面的方式，因为它们引入了额外的参数量和计算复杂度。

最后，我们的方法似乎是对现有方法的补充，其他的空间卷积核，如 3x1 和 1x3，也可以被用在第一次组卷积中，将 3x3的卷积核分成两个连续的卷积核- 3x1 和 1x3。这些都增加了进一步提高参数效率的可能。

5. Experiments

5.1 Datasets

• CIFAR-10和CIFAR-100中使用了数据增强；
• SVHN没有使用数据增强；

5.2 实现细节

• IGC + BN + ReLU；
• 使用SGD算法，从头开始训练网络；
• 权重衰减率为0.0001，动量为0.9；
• 在CIFAR-10和CIFAR-100中，我们迭代400次，mini-batch为64，在两块GPU上同时训练，初始学习率为0.1，且衰减因子为10；
• 在SVHN中，我们迭代40次，mini-batch为64，在两块GPU上同时训练，初始学习率为0.1，衰减因子为10；

5.3 实验研究