作业涉及的MATLAB常用方法举例

前言

作为控制学科的学生，在一年级的课程当中会涉及到一些MATLAB相关的作业，会用到一些常用的方法，如求解常微分方程、传递函数与状态空间方程、最小二乘法、模糊控制、曲线绘制等。为避免重复造轮子，还是有必要将这些简单的方法记录下来的。那么话不多说，接下来开始分部分进行叙述。

常微分方程求解

MATLAB内置有不少求解常微分方程的函数，如ode23、ode45、ode113、ode23t、ode15s、ode23s、ode23tb等，各个函数使用不同的方法求解，精度与速度也有一定的区别，其中最常用的是ode45。以ode45举例来说，假设我们需要求解方程dy=-y+y^2，那么使用相应的代码如下：

odefun=@(t,y)-y+y^2; % 微分方程dy=-y+y^2
y0=[0.5]'; % 变量初值
[t,y]=ode45(odefun,[0 5],y0); % 调用ode45求解

如果需要求解常微分方程组，那么可单独定义odefun函数，再调用ode45求解。例如求解如下微分方程组：
dy1=y2
dy2=6sin(t)-0.1y2-y1^5
则相应的MATLAB代码如下：

% @odefun.m
function dy = odefun(t, y)
	dy=zeros(2,1);
	dy(1)=y(2);
	dy(2)=6*sin(t)-0.1*y(2)-y(1)^5;
end
% @ode45test.m
y0=[0.5 0.5]';
[t,y]=ode45(odefun,[0 5],y0);

传递函数与状态方程

传函和状态方程可以说是控制专业中接触最频繁的概念之一，MATLAB也内置了近乎完善的一套方法来处理相关的问题，可以说是五花八门，应有尽有。这里我仅记录最近两次作业涉及到的一点方法，其他的方法暂无讨论。
首先是根据数组num，den定义传递函数G，用到的方法是tf。例如传递函数为G=(s+5)/(s^2+5s+3)，那么定义传递函数的代码如下：

num=[1 5];
den=[1 5 3];
G=tf(num,den);

如需通过传递函数获取对应的状态空间方程，则可使用tf2ss函数进行转换，对应的也可使用ss2tf函数进行状态空间方程到传递函数的变换，具体代码如下：

[A,B,C,D]=tf2ss(num,den);
[num,den]=ss2tf(A,B,C,D,iu); % iu指定获取第几个输出对应的传递函数（对应传递函数阵的情况）

如需获取传递函数的阶跃响应，可使用step函数求得，具体的代码如下：

[y,t]=step(G,[0 10]); % 获取10秒内的传递函数阶跃响应

上面的式子是直接求取一段时间内的阶跃响应，且输入固定为1。但如需用递推的方式求得指定输入信号作用下的系统输出时，可首先转换传递函数到状态空间方程，再调用c2d函数对状态方程进行指定采样周期下的离散化。具体的代码如下：

Ts=1; % 指定采样周期为1秒
[As,Bs,Cs,Ds]=tf2ss(num,den);
[Ad,Bd]=c2d(As,Bs,Ts); % 对As和Bs矩阵进行离散化，Cs和Ds无需操作
xs0=[0 0]'; % 指定状态初值（二阶系统）
% 状态空间方程的递推公式
xs1=Ad*xs0+Bd*u(k);
y(k)=Cs*xs1+Ds*u(k);
xs0=xs1;

如果需要通过传递函数判断系统的稳定性，可直接调用roots函数对传递函数分母求特征根，再调用real函数取复数根的实部并对实部进行判断，如果存在大于0则表示系统不稳定。具体的代码如下：

p=real(roots(den)); % 求传递函数的特征根实部
for k=length(p)
    if p(k)>0
        error('系统模型不稳定');
    end
end

最小二乘法

最小二乘法（LS）是数据拟合的经典方法之一，可以说是经久不衰，简单实用。关于LS的推导这里不做叙述，这里直接以一个较完整的例子给出，简单直白粗暴。假设我们有如下数据序列：
x=[1 2 3 4 5];
y=[4 4.5 6 8 8.5];
我们的目标是用一条直线y=a0+a1x来拟合这些数据，那么具体的代码如下：

x=[1 1 1 1 1;1 2 3 4 5;]'; % 输入数据（a0对应全1向量，a1对应x向量）
y=[4 4.5 6 8 8.5]'; % 输出数据
z=(x'*x)^-1*x'*y; % LS拟合参数
a0=z(1);
a1=z(2);

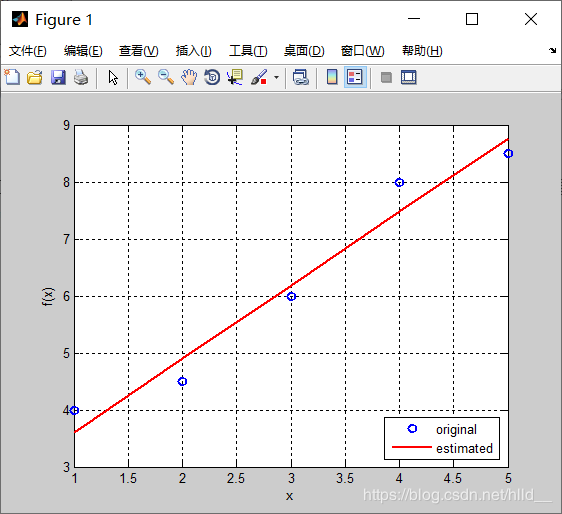
其中上式得到的a0和a1既是拟合后直线方程的系数，将原数据点与拟合后得到的直线绘制图形进行对比如下：

某些情况下，我们用于拟合的数据可能是有不同权重的，那么就涉及到加权最小二乘法（WLS）的使用。具体的推导过程依然省略，还是以上面的数据为例，假设数据对应的权重序列为w=[2 1 3 1 1]，那么对应的加权最小二乘拟合代码如下：

w=[2 1 3 1 1]'; % 拟合数据权重
W=diag(w); % 权重矩阵
z=(x'*W^-1*x)^-1*x'*W^-1*y; % WLS拟合参数
a0=z(1);
a1=z(2);

经过加权拟合后的直线与原数据点的图形如下，可看到两者之间的结果有细微的差别：

模糊控制

使用MATLAB实现简单的模糊控制是极为简单的事情，不论是调用m文件的内置函数还是使用Simulink仿真都可以实现想要的功能。这里首先介绍使用MATLAB的fuzzy box工具箱进行简单的模糊控制器设计，然后介绍在m文件中调用设计的模糊控制器，最后用一个简单的Simulink例子来介绍模糊控制器的仿真。

模糊控制器的设计

使用fuzzy box工具箱设计模糊控制器，简单的方式是在MATLAB命令行窗口输入命令fuzzy，即可打开工具箱的FIS Editor界面如下：

工具箱中默认的与算子（And）方法为min，或算子（Or）方法为max，解模糊（Defuzzification）方法为centroid（质心法），这些设置一般不用改动，保持默认即可。通常模糊控制器的输入为误差E和误差的微分EC，如需添加模糊控制器的输入输出变量，可点击菜单Edit->Add Variable->Input/Output选项。如需删减控制器变量，则可先选中该变量，然后点击Edit->Remove Selected Variable选项。在确定输入输出变量的个数以及变量名称后，可双击左上或右上的方框，或者点击Edit->Membership Function Editor选项，打开编辑模糊控制器输入输出隶属度函数的Membership Function Editor界面进行设计，其界面如下：

在变量的编辑页面下方，可以选择变量的取值范围（Range）。MATLAB默认生成的变量包含三个隶属度函数mf1、mf2和mf3，一般我们需要删除它们然后重新指定一组隶属度函数。可点击菜单Edit->Remove Selected MF选项删除选中的隶属度函数，也可点击Edit->Remove All MFs选项删除选中变量的全部隶属度函数。然后可点击Edit->Add MFs选项进入编辑页面选择添加一组隶属度函数，需要选择的参数有隶属度函数类型（MF Type）和隶属度函数的个数（Number of MFs）。其中隶属度函数类型通常选三角形（trimf），函数个数通常选7。也可以点击Edit->Add Custom MF选项添加自定义的隶属度函数。
在完成变量及隶属度函数的指定后，即可根据模糊控制的专家规则进行规则（Rules）的添加。可双击FIS Editor界面输入输出变量中间的空白，或者点击菜单Edit->Rules选项打开规则编辑界面如下：

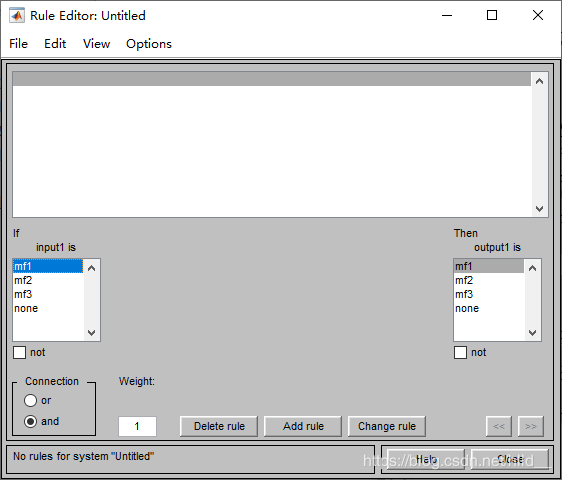
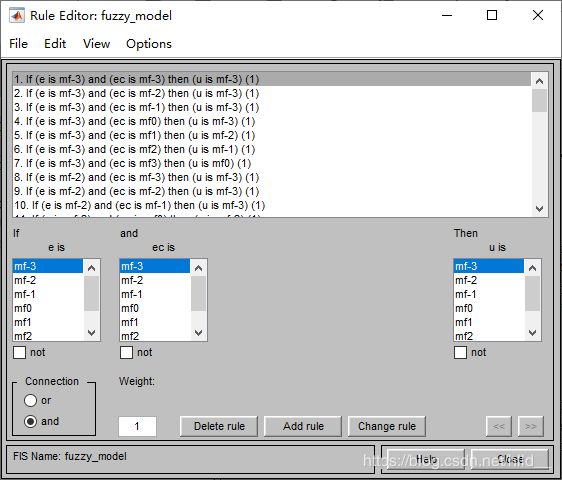
控制规则的典型语句为If A then C或者If A and B then C，通常我们需要的专家规则都能从文献中找到，如典型的49条规则如下：

在上图中，模糊控制器的输入设定为误差E和误差的微分EC，输出为控制率U，且每个变量的模糊论域分为7个模糊子集，既NB（负大）、NM（负中）、NS（负小）、ZO（零）、PS（正小）、PM（正中）、PB（正大）。将这些规则添加到模糊控制器中的语句为：If E is NB and EC is NB then U is NB等等，共49条规则。在规则依次录入后，简单的模糊控制器就已设计完毕，可点击菜单File->Export->To Workspace/To File选项导出模型到工作区或者导出到.fis文件。如需之后再微调，则可以重新打开fuzzy box点击File->Import->From Workspace/File选项加载已设计好的模型到工具箱。这里贴出设计好的一个简单模糊控制器的截图：

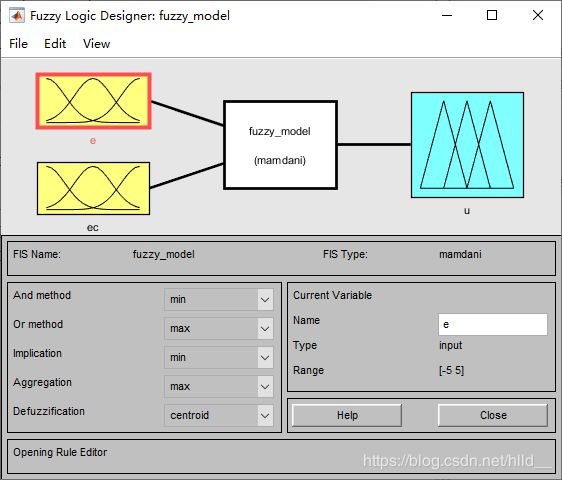
模糊控制器的仿真

在设计好模糊控制器后，即可对控制器进行仿真验证，MATLAB主要提供两种仿真的方式，一种是在m文件中进行仿真，一种是搭建Simulink模型进行仿真。首先介绍m文件的模糊控制器仿真方式。
在m文件中仿真需要用到两个函数，分别是readfis和evalfis。其中readfis用于读取我们设计好的.fis模型文件，evalfis则用于计算模糊控制器在给定输入值下的输出，简单的测试代码如下：

fismat=readfis('fuzzy_model.fis');
E=[2.1 4.0]';
EC=[4.2 9.0]';
input=[E EC];
output=evalfis(input,fismat); % output=[2.8723 3.7500]'

同样也可以使用Simulink的模糊控制器模块对控制器进行仿真，简单的仿真图如下所示：

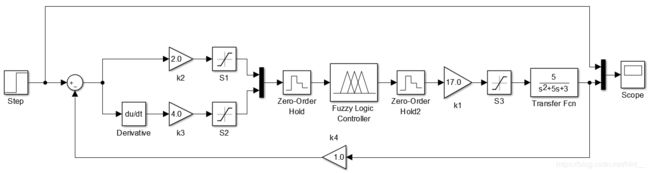
在上图中，模糊控制器的输入分别为误差和误差的微分，输出则直接作用在二阶被控对象上。为保持控制器的输入在设计时确定的取值范围内，这里分别用S1和S2两个饱和模块限制输入的上限和下限。同样地，在输出端也设置一个门限，确保控制器的输出不会超过指定的范围。需要主要的是，最好在模糊控制器两端加上零阶保持器，这样可以使得仿真顺利运行。其中模糊控制器模块的编辑界面如下：

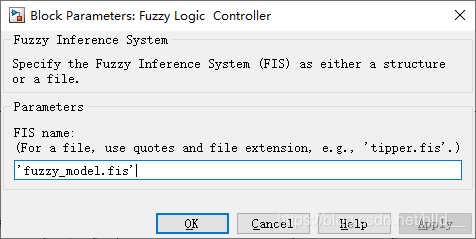
曲线绘制

通常我们完成仿真后会使用plot函数绘制结果曲线，简单的绘图一般包括单张画布绘制多条曲线和单张画布绘制多个子图两种情况。这里分别通过简单的例子进行演示。
首先是单张画布绘制多条曲线的情况。为了简单，我i们直接用上面最小二乘法例子中的x和y序列以及y-1序列为例，既x=[1 2 3 4 5]，y1=[4 4.5 6 8 8.5]，y2=[3 3.5 5 7 7.5]。绘制曲线的代码及绘制的曲线如下所示：

x = [1 2 3 4 5];
y1=[4 4.5 6 8 8.5];
y2=[3 3.5 5 7 7.5];
figure(1);
plot(x, y1, 'b', 'linewidth', 2); % 参数'b'：蓝色，'linewidth', 2：设置线宽为2
hold on; % 准备绘制下一条曲线
plot(x, y2, '-r', 'linewidth', 2); % 参数'-'：绘制实线风格，参数'r'：红色
grid on; % 绘制栅格
xlabel('x') % 设置x轴标签
ylabel('y') % 设置y轴标签
legend('y1', 'y2') % 设置说明文字

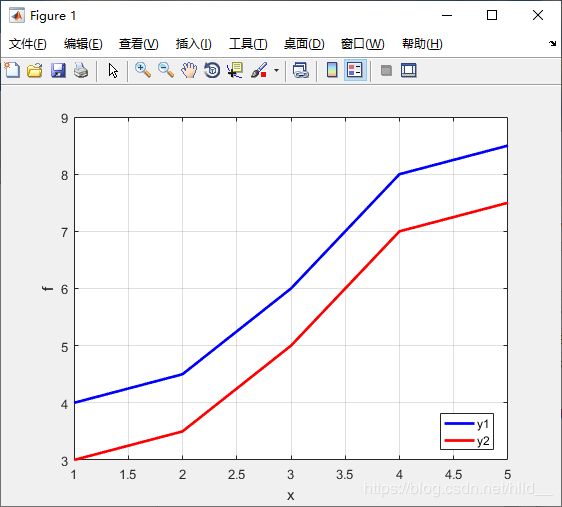
要注意的仅是绘制下一条曲线的时候需要调用hold on，调用plot函数的时候x坐标可以不用给出，函数可以自动生成x坐标。plot函数绘制曲线有多种风格可选，其源码文件注释的风格如下：

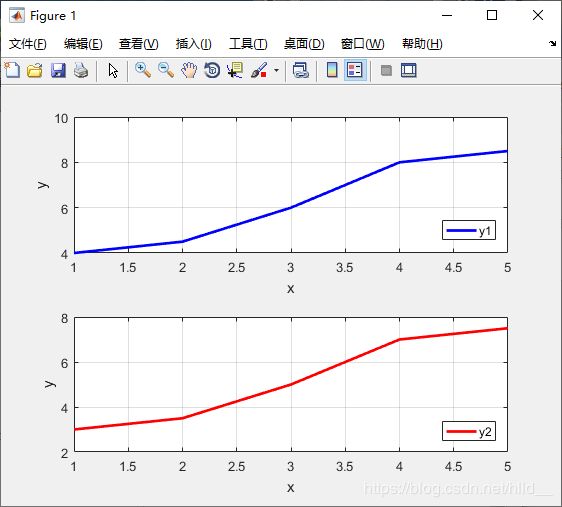
在此基础上，通过简单的修改即可实现单张画布绘制多个子图，绘图的代码及绘制的曲线如下所示：

figure(1);
subplot(211); % 创建2行1列子画布集，并选择从左到右，从上到下的第一个子画布绘制曲线
plot(x, y1, 'b', 'linewidth', 2);
grid on;
xlabel('x');
ylabel('y');
subplot(212); % 选择第二个子画布绘制曲线
plot(x, y2, '-r', 'linewidth', 2);
grid on;
xlabel('x');
ylabel('y');

结束语

算是一点积累吧，虽然没有太多价值，但总比没有好。通过记录一些工作可以避免重复造轮子，提高工作效率，毫无疑问是一个好习惯。记录一点点也许还能帮助到有需要的人，何乐而不为呢。不说了，又是新的一天，新的工作。