SDOI2013 淘金

题目描述

小 Z在玩一个 叫做《淘金者》的游戏。游戏的世界是一个 二维坐标 。 X轴、Y轴 坐标范围均为 1..N 。初始的时候，所有的整数坐标点上均有一块金子，共 N∗N 块。

一阵风吹过， 金子的位置发生了一些变化。细心的小Z发现， 初始 在 (i,j) 坐标 处的金子会变到 (f(i),f(j)) 坐标 处。其中 f(x) 表示 x 各位数字的乘积 ，例如 f(99)=81，f(12)=2，f(10)=0 。如果金子变化后的坐标不在 1..N 的范围内，我们认为这块金子已经 被移出游戏。 同时可以发现， 对于变化之后的游戏局面， 某些 坐 标上的金子数量可能 不止一块 ，而另外一些坐标上可能已经没有金子 。这次变化 之后， 游戏将不会再对 金子的位置和数量进行改变，玩家可以开始采集工作。

小 Z很懒 ，打算 只进行 只进行 K 次采集 。每次采集可以得到某 一个坐标上的所有 金子 ，采集之后该坐标上的金子数变为 0。

现在小 Z希望知道，对于变化之后的游戏局面，在采集次数为 K 的前提下， 最多可以采集到少块金子？

答案可能很大，小 Z希望得到 1000000007(109+7) 取模之后的答案。

Input

共一行，包含两个正整数 N, K 。

Output

一个整数 ，表示最多可以采集到的金子数量。

Sample Input

12 5

Sample Output

18

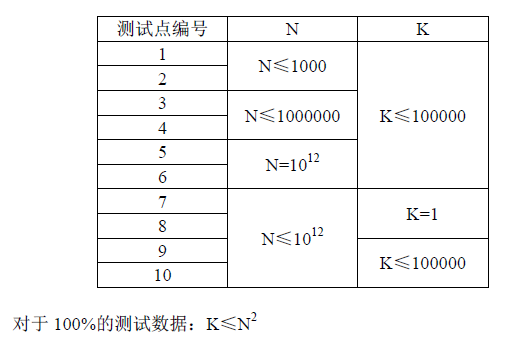
数据范围

样例解释

题解

我们可以发现 x,y 坐标是不相关的。
我们设 y=f(x) 接下来我们的任务就是求 y 的个数。
易得， y 可以表示成 2p1∗3p2∗5p3∗7p4 ,又可得 y 的数量很少，只有大概20000个。我们就顺理成章想到用数位dp了。

设状态 Fi,j,k 表示从高至低dp到第 i 位，前 i 位的积为 j ，前 i 位是否与原数的前 i 位相同(这一位只有0或1)。

Fi,j,0⇒Fi+1,j∗k,0,1⩽k⩽9

Fi,j,1 的情况读者可以自己推一下。

参考代码

#include
#include
#include
#include
#include
#include
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define maxn 20
#define ll long long
#define mo 1000000007
using namespace std;

ll n,m;

ll f[1000005];

ll num[20];

struct note1{
    ll a,b;
};

queue now,next;

map  g[20];

bool operator < (const note1 a,const note1 b){
    if(a.a!=b.a)return a.areturn a.b < b.b;
}

void add(int x,note1 pq,ll ad) {
    if (!g[x].count(pq)) 
        next.push(pq);
    g[x][pq]+=ad;
}

void Pre(ll n){
    ll t1=0,t2=0;
    while (n) {
        num[++num[0]]=n % 10;
        n /= 10;
    }
    note1 tmp;
    tmp.a=0;
    tmp.b=1;
    now.push(tmp);
    g[num[0]+1][tmp]=1;
    fd(i,num[0],1) {
        while (!now.empty()) {
            note1 tmp=now.front();
            now.pop();
            ll way=g[i+1][tmp];
            if (!tmp.a) {
                fo(j,1,num[i]) {
                    if (j==num[i]) {
                        note1 pq;
                        pq.a=0;
                        pq.b=tmp.b*j;
                        add(i,pq,way);
                    }
                    else {
                        note1 pq;
                        pq.a=1;
                        pq.b=tmp.b*j;
                        add(i,pq,way);
                    }
                }
            }
            else {
                fo(j,1,9){
                    note1 pq;
                    pq.a=1;
                    pq.b=tmp.b*j;
                    add(i,pq,way);
                }
            }
        }
        note1 tmp;
        tmp.a=1;
        tmp.b=1;
        if (i>1) add(i,tmp,1);
        while (!next.empty()) {
            note1 tmp=next.front();
            next.pop();
            if (i==1&&!tmp.a) t1=tmp.b,t2=g[1][tmp];
            now.push(tmp);
        }
    }
    while (!now.empty()) {
        note1 tmp=now.front();
        now.pop();
        if (tmp.a==0) continue;
        f[++f[0]]=g[1][tmp];
        if (tmp.b==t1) f[f[0]]+=t2,t1=0;
    }
    if (t1>0) f[++f[0]]=t2;
}

bool cmp(int i,int j){
    return i>j;
}

struct note{
    ll w;
    int x,y;
};

bool operator < (note i,note j){
    return i.w q;

void main2(){
    fo(i,1,f[0]) {
        note tmp;
        tmp.w=f[i]*f[1];
        tmp.x=i;
        tmp.y=1;
        q.push(tmp);
    }
    ll ans=0;
    fo(i,1,m) {
        if (q.empty()) break;
        note now=q.top();
        q.pop();
        ans=(ans+now.w) % mo;
        if (now.y!=f[0]) {
            now.w=f[now.x]*f[now.y+1];
            now.y++;
            q.push(now);
        }
    }
    printf("%lld",ans);
}

int main(){
    scanf("%lld%lld",&n,&m);
    Pre(n);
    sort(f+1,f+f[0]+1,cmp);
    main2();
    return 0;
}