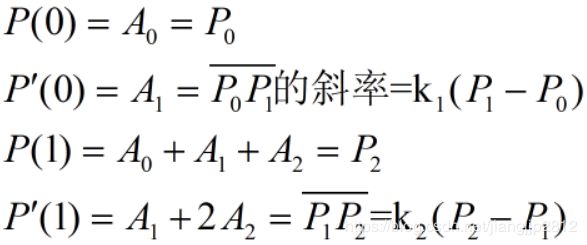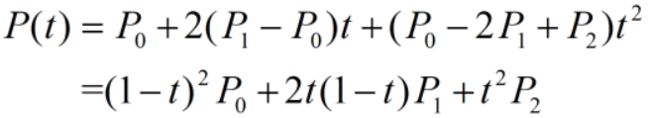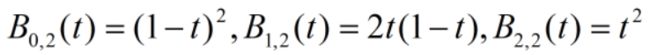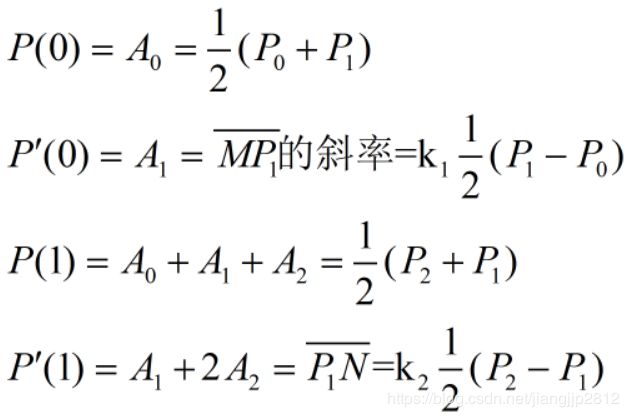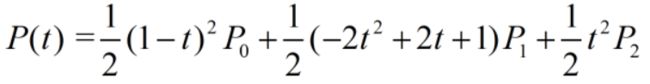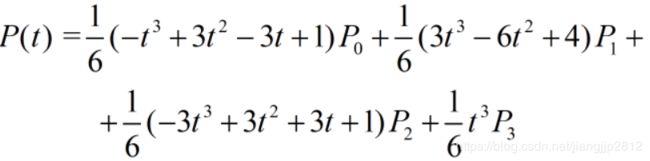二次与三次B样条曲线c++实现
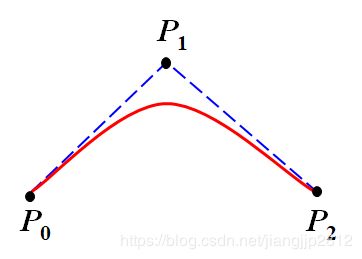
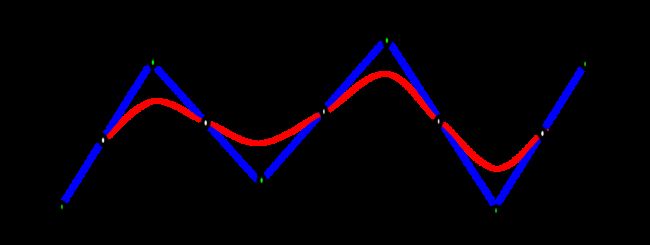
B样条曲线构建一条平滑曲线,接近而不通过控制点(首尾点除外)。如图
B样条曲线从Bezier曲线演变而来,了解B样条曲线首先得了解Bezier曲线。对于平面上的三个点P0,P1,P2,其坐标分别是(x0,y0)、(x1,y1)、(x2,y2)。二次Bezier曲线用一条抛物线进行拟合,其参数方程是
二次Bezier曲线有如下要求:(1)t=0时,曲线经过P0,并与P0P1相切;(2)t=1时,曲线经过P2,并与P1P2相切。即有
联立这些条件可以得到曲线参数表达式:
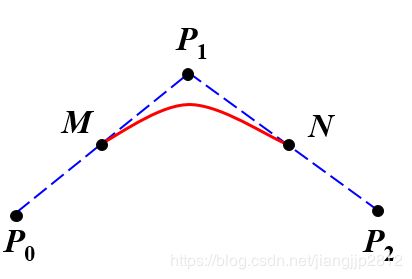
每3个离散点形成一条Bezier曲线,由于每条Bezier都经过端点,导致分段的Bezier曲线在端点处难以平滑过渡。二次B样条曲线克服了这个缺点,把端点移到线段中点(如下图所示),这样就能保证各段曲线在连接处能够一阶导数连续。
由此满足条件:
结合条件可以求解得到二次B样条曲线:
二次B样条曲线实现,只需将曲线参数t划分成k等分,t从0开始取值,间隔dt,直至k*dt。如果想让整条曲线两端与起始点P0和终止点Pn重合,只需以P0和Pn为中点,构造新点PP1=2*P0-P1,与PP2=2*Pn-Pn-1,替换掉P0与Pn即可。
三次B样条曲线通过样条基函数可以得到如下形式:
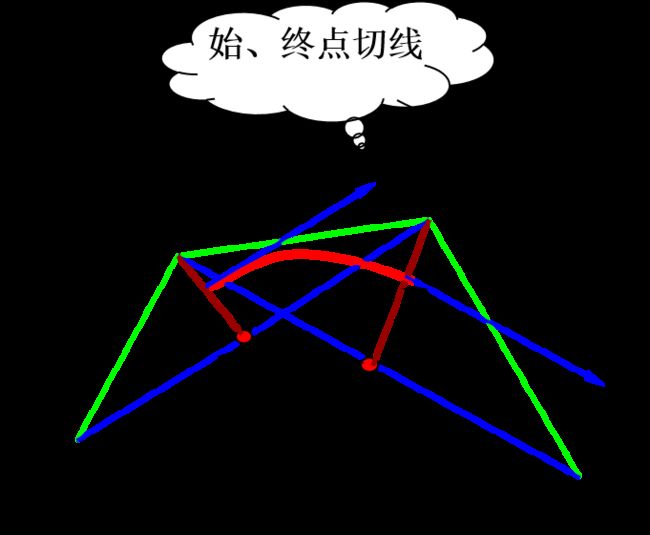
三次B样条具有以下物理意义,曲线起点S位于三角形P0P1P2的中线P1M1上,距离P1点1/3倍P1M1处;曲线中点E位于三角形P1P2P3的中线P2M2上,距离1/3倍P2M2处;曲线起点切线平行于P0P2,终点切线平行于P1P3.
三次B样条曲线要想让曲线两端与起始端P0与Pn重合,只需构造新点PP1=2*P0-P1,与PP2=2*Pn-Pn-1,分别加到P0之前与Pn之后即可。由此,参与计算点的增加了2个(注意,二次B样条是替换不是增加)。
编程实现:
程序实现了二次与三次B样条曲线,封装成了BSpline类
BSpine.h
#pragma once
//#include "position.h"
typedef struct tagPosition
{
double x;
double y;
tagPosition(double _x,double _y) { x=_x; y=_y;}
tagPosition() {};
bool operator==(const tagPosition & pt) { return (x==pt.x && y==pt.y);}
} CPosition;
class CBSpline
{
public:
CBSpline(void);
~CBSpline(void);
void TwoOrderBSplineSmooth(CPosition *pt,int Num);
void TwoOrderBSplineInterpolatePt(CPosition *&pt,int &Num,int *InsertNum);
double F02(double t);
double F12(double t);
double F22(double t);
void ThreeOrderBSplineSmooth(CPosition *pt,int Num);
void ThreeOrderBSplineInterpolatePt(CPosition *&pt,int &Num,int *InsertNum);
double F03(double t);
double F13(double t);
double F23(double t);
double F33(double t);
};BSpine.cpp
//**************************** BSpline.cpp ***********************************
// 包含功能:二次B样条平滑,三次B样条平滑;二次B样条平滑后节点插值
//
// 作者: 蒋锦朋 [email protected]
// 单位: 中国地质大学(武汉) 地球物理与空间信息学院
// 日期: 2014/12/03
//*************************************************************************************
#include "StdAfx.h"
#include "BSpline.h"
CBSpline::CBSpline(void)
{
}
CBSpline::~CBSpline(void)
{
}
//======================================================================
// 函数功能: 二次B样条平滑,把给定的点,平滑到B样条曲线上,不增加点的数目
// 输入参数: *pt :给定点序列,执行完成后,会被替换成新的平滑点
// Num:点个数
// 返回值: 无返回值
// 编辑日期: 2014/12/03
//======================================================================
void CBSpline::TwoOrderBSplineSmooth(CPosition *pt,int Num)
{
CPosition *temp=new CPosition[Num];
for(int i=0;i程序调用:
#include "stdafx.h"
#include "math.h"
#include "BSpline.h"
int _tmain(int argc, _TCHAR* argv[])
{
int num=8;
double x[8]={9.59,60.81,105.57,161.59,120.5,100.1,50.0,10.0};
double y[8]={61.97,107.13,56.56,105.27,120.5,150.0,110.0,180.0};
CPosition *testpt=new CPosition[num];
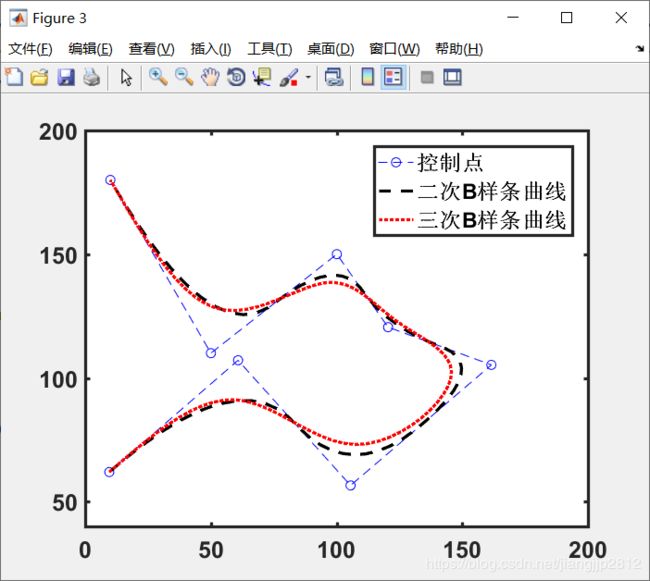
for(int i=0;i程序运行结束后会生成样条曲线坐标文件,分别为横坐标:Bspline_test_x.txt和纵坐标Bspline_test_y.txt.利用matlab绘图可以得到下面结果:
附matlab绘图代码:
clear all;
clc;
load Bspline_test_x2.txt; % 导入二次B样条计算的结果
load Bspline_test_y2.txt;
load Bspline_test_x3.txt; % 导入三次B样条计算的结果
load Bspline_test_y3.txt;
control_point_x=[9.59,60.81,105.57,161.59,120.5,100.1,50.0,10.0];
control_point_y=[61.97,107.13,56.56,105.27,120.5,150.0,110.0,180.0];
figure;
h1=plot(control_point_x,control_point_y,'--ob'); hold on;
h2=plot(Bspline_test_x2,Bspline_test_y2,'--k','LineWidth',2);
h3=plot(Bspline_test_x3,Bspline_test_y3,':r','LineWidth',2);
legend([h1 h2 h3],'控制点','二次B样条曲线','三次B样条曲线');
axis([0 200 40 200]);
set(gca,'FontSize',15); set(gca,'FontWeight','bold'); set(gca,'LineWidth',2);
set(get(gca,'XLabel'),'Fontsize',15); set(get(gca,'YLabel'),'FontSize',15);