哈夫曼编码以及解码的java程序实现（附完整代码）

本文引用自这篇博客

什么是霍夫曼编码

哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最 佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）

简单来说，若在一个字符串中，知道每个字母各自出现的频率，通过将出现频率较大的字符采用较少位数来编码的方式达到压缩的目的，即一个字符出现的频次越大，它的编码位数应该更少。

编码过程和实例

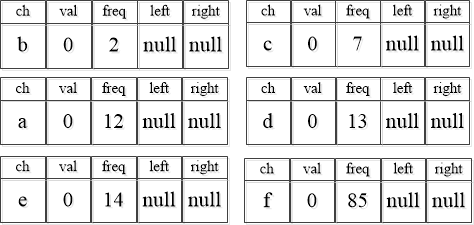
假设在一个文件中，字符集的频率如下表

字符	a	b	c	d	e	f
频次	12	2	7	13	14	85

首先，利用上表为每一个字符创建一颗二叉树，并将其出现频次存储在节点中，节点数据结构定义为TreeNode

private class TreeNode {
    public TreeNode() { }
    public TreeNode(Character ch, int val, int freq, TreeNode left, TreeNode right) {
        this.ch = ch;
        this.val = val;
        this.freq = freq;
        this.left = left;
        this.right = right;
    }
	//ch存储当前节点字符，若没有，则为null
    Character ch;
	//只有两个值：0或1，若在构建二叉树的过程中该节点为左节点，则val=0,反之，val=1
    int val;
	//存储字符出现的频次
    int freq;
	//左节点
    TreeNode left;
	//右节点
    TreeNode right;
}

分别为a、b、c、d、e、f创建初始化二叉树节点，如下图所示：

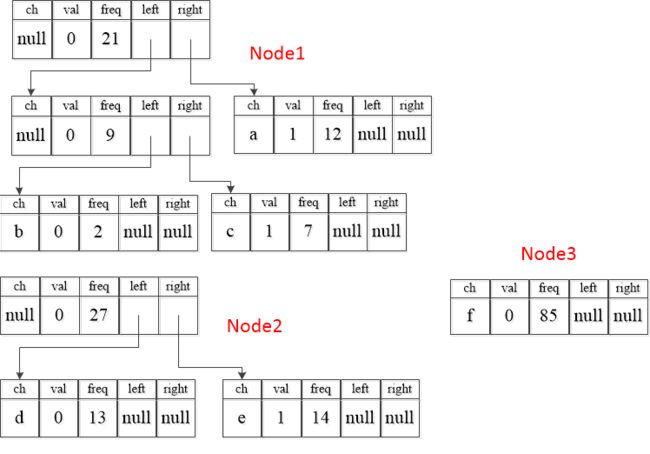
在列表中寻找根节点中存有最小频率值的两颗二叉树，创建一个不存储任何字符的节点，将这两颗二叉树作为新建节点的左右子树，并将其频次值之和存储到新建节点中。在这6个节点中，频次之和最小的两个是b、c，将左节点的val更新为0，右节点的val更新为1，合并为一个新的二叉树，如下：

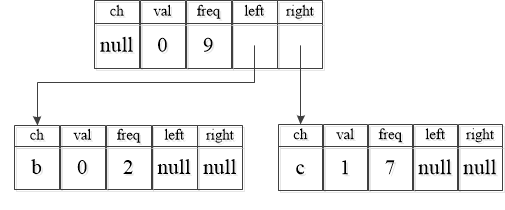
上面得到的新节点的freq=9，与剩下的a、d、e、f放在一起可以发现，9+12=21为最小频次，即需要频次为9的二叉树与频次为12的二叉树进行组合。结果如下：

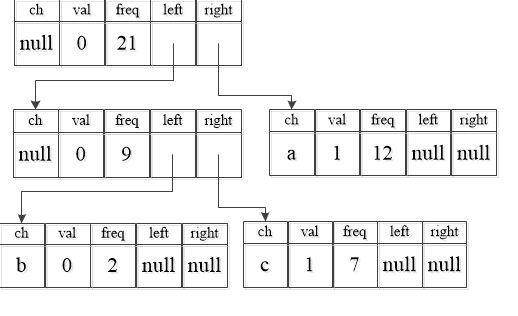
新节点freq=21,剩下的d、e、f频次分别为13、14、85，可以看到13+14=27最小，所以接下来组合d、e，组合之后，所有剩余的二叉树节点如下图所示：

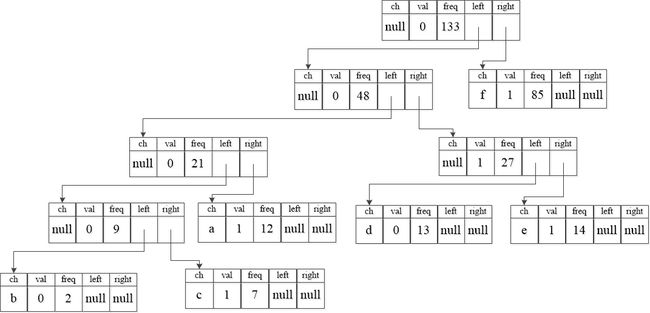
一直重复上述步骤、可得到一个最终的二叉树如下：

得到最终的二叉树后，就可以进行编码了，依次遍历二叉树的每一条路径，取每个节点的val值，遍历到叶结点后，叶结点ch值所对应的的路径去除第一个字符即为该字符的编码，例如：
第一个叶结点对应的字符为b，对应的路径为00000,去除第一个字符后，可得最终编码为0000,同理可得a对应的编码为001。所有字符的编码结果如下：

字符	a	b	c	d	e	f
出现频次	12	2	7	13	14	85
编码后	001	0000	0001	010	011	1

java程序实现

import java.util.*;
import org.junit.Test;

public class Huffman {
	//内部类 二叉树节点
    private class TreeNode {
        public TreeNode() { }
        public TreeNode(Character ch, int val, int freq, TreeNode left, TreeNode right) {
            this.ch = ch;
            this.val = val;
            this.freq = freq;
            this.left = left;
            this.right = right;
        }
        Character ch;
        int val;
        int freq;
        TreeNode left;
        TreeNode right;
    }
	
    @Test
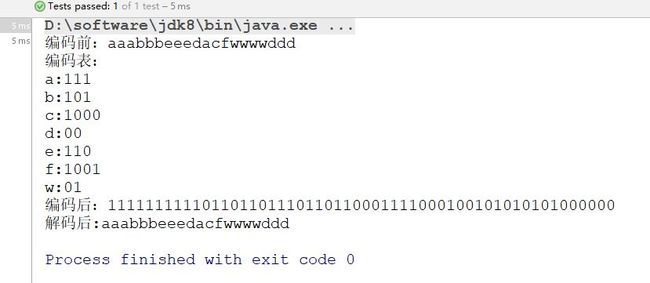
    public void testEncode(){
        String s = "aaabbbeeedacfwwwwddd";

        System.out.println("编码前："+s);

        Object[] encodeRes = encode(s);
        String encodeStr = (String)encodeRes[0];
        Map<Character,String> encodeMap = (Map<Character, String>)encodeRes[1];

        System.out.println("编码表：");
        for(Map.Entry<Character,String> e:encodeMap.entrySet()){
            System.out.println(e.getKey()+":"+e.getValue());
        }
        System.out.println("编码后："+encodeStr);

        String decodeStr = decode(encodeStr,encodeMap);
        System.out.println("解码后:"+decodeStr);
    }
	
	//编码方法，返回Object[]，大小为2,Objec[0]为编码后的字符串，Object[1]为编码对应的码表
    public Object[] encode(String s){
        Object[]res= new Object[2];
        Map<Character,String> encodeMap = new HashMap<Character, String>();
        TreeNode tree = constructTree(s);
        findPath(tree, encodeMap, new StringBuilder());
        findPath(tree, encodeMap, new StringBuilder());
        StringBuilder sb = new StringBuilder();
        for(int i=0;i<s.length();i++){
            String tmp = encodeMap.get(s.charAt(i));
            sb.append(tmp);
        }
        res[0]=sb.toString();
        res[1] = encodeMap;
        return res;

    }
	
	/*
	* 根据字符串建立二叉树
	* @param s：要编码的源字符串
	*/
    private TreeNode constructTree(String s) {
        if (s == null || s.equals("")) {
            return null;
        }
        //计算每个字母的词频，放到Map中
        Map<Character, Integer> dataMap = new HashMap<Character, Integer>();
        for (int i = 0; i < s.length(); i++) {
            Character c = s.charAt(i);
            if (dataMap.containsKey(c)) {
                int count = dataMap.get(c);
                dataMap.put(c, count + 1);
            } else {
                dataMap.put(c, 1);
            }
        }
        //遍历dataMap,初始化二叉树节点，并将所有初始化后的节点放到nodeList中，并进行排序
        LinkedList<TreeNode> nodeList = new LinkedList<TreeNode>();
        for (Map.Entry<Character, Integer> entry : dataMap.entrySet()) {
            Character ch = entry.getKey();
            int freq = entry.getValue();
            int val = 0;
            TreeNode tmp = new TreeNode(ch,val,freq,null,null);
            nodeList.add(tmp);
        }
		//对存放节点的链表进行排序，方便后续进行组合
        Collections.sort(nodeList, new Comparator<TreeNode>() {
            public int compare(TreeNode t1, TreeNode t2) {
                return t1.freq-t2.freq;
            }
        });

        //size==1,代表字符串只包含一种类型的字母
        if(nodeList.size()==1){
            TreeNode t = nodeList.get(0);
            return new TreeNode(null,0,nodeList.get(0).freq,t,null);
        }

        //利用排序好的节点建立二叉树，root为初始化根节点
        TreeNode root = null;
        while(nodeList.size()>0){
			//因为nodeList在前面已经排好序，所以直接取出前两个节点，他们的和肯定为最小
            TreeNode t1 = nodeList.removeFirst();
            TreeNode t2 = nodeList.removeFirst();
			//左子树的val赋值为0，右子树的val赋值为1
            t1.val = 0;
            t2.val = 1;
			//将取出的两个节点进行合并
            if(nodeList.size()==0){
				//此时代表所有节点合并完毕，返回结果
                root = new TreeNode(null,0,t1.freq+t2.freq,t1,t2);
            }else {
				//此时代表还有可以合并的节点
                TreeNode tmp = new TreeNode(null,0,t1.freq+t2.freq,t1,t2);
				
                //t1、t2合并后，需要将得到的新节点加入到原链表中，继续与其他节点合并，
				//此时需要保证原链表的有序性，需要进行排序
                if(tmp.freq>nodeList.getLast().freq){
                    nodeList.addLast(tmp);
                }else {
                    for(int i=0;i<nodeList.size();i++){
                        int tmpFreq = tmp.freq;
                        if(tmpFreq<= nodeList.get(i).freq){
                            nodeList.add(i,tmp);
                            break;
                        }
                    }
                }
            }
        }
		//返回建立好的二叉树根节点
        return root;
    }
	
	//对已经建立好的二叉树进行遍历，得到每个字符的编码
    private void findPath(TreeNode root, Map<Character,String> res, StringBuilder path) {
        if (root.left == null && root.right == null) {
            path.append(root.val);
            res.put(root.ch,path.substring(1));
            path.deleteCharAt(path.length() - 1);
            return;
        }
        path.append(root.val);
        if (root.left != null) findPath(root.left, res, path);
        if (root.right != null) findPath(root.right, res, path);
        path.deleteCharAt(path.length() - 1);
    }
	
	//对字符串进行解码，解码时需要编码码表
	public String decode(String encodeStr,Map<Character,String> encodeMap){
        StringBuilder decodeStr = new StringBuilder();
        while(encodeStr.length()>0){
            for(Map.Entry<Character,String> e: encodeMap.entrySet()){
                String charEncodeStr = e.getValue();
                if(encodeStr.startsWith(charEncodeStr)){
                    decodeStr.append(e.getKey());
                    encodeStr = encodeStr.substring(charEncodeStr.length());
                    break;
                }
            }
        }
        return decodeStr.toString();
    }
	
}

运行测试用例