LFSR:线性反馈移位寄存器及其应用
LFSR简介
LFSR(Linear-feedback shift register)是一种特殊的的移位寄存器,他的输入取决于其先前状态。
LFSR的使用异常广泛,可以说涉及到方方面面,以下是Wikipedia列举的一些应用
- INTELSAT business service (IBS)
- Intermediate data rate (IDR)
- SDI (Serial Digital Interface transmission)
- Data transfer over PSTN (according to the ITU-T V-series recommendations)
- CDMA (Code Division Multiple Access 码分多址) cellular telephony
- 100BASE-T2 “fast” Ethernet scrambles bits using an LFSR
- 1000BASE-T Ethernet, the most common form of Gigabit Ethernet, scrambles - bits using an LFSR
- PCI Express 3.0
- SATA
- Serial attached SCSI (SAS/SPL)
- USB 3.0
- IEEE 802.11a scrambles bits using an LFSR
- Bluetooth Low Energy Link Layer is making use of LFSR (referred to as whitening)
- Satellite navigation systems such as GPS and GLONASS
事实上LFSR在上述系统中更广为人知的应用是伪随机数的生成与CRC计算。
以下来自Wikipedia的动图展示了LFSR的一个有趣的应用。
这是一个使用LSFR构建的31位伪随机数发生器,LED充当了其输出。原作者使用了4块74HC565(这个IC查不到,应该是作者看错了)和一块74HC86(异或门)。
对于一个LFSR,其可以看作一个FSM。这个LFSR最多状态数为
2 n − 1 2^n -1 2n−1
那么对于上面那个31位的LFSR,有多达2,147,483,6487个状态,假如一个状态持续0.2秒,那么需要长达13.61925年这个状态机才能重新回到初始状态!
LFSR的实现
LFSR可以使用若干个寄存器和异或门组成,其结构也不同,这里列举其中两个。
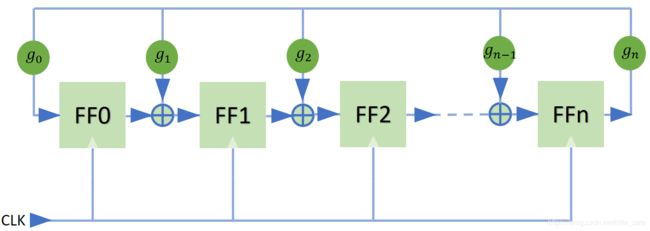
Galois型
Fibonacci型

当然这两种无论哪一种都是比较方便用HDL语言或者其他语言实现的。
我们以一个简单的3位Galois型LFSR为例。

注意这里 g 0 = 1 g_0 = 1 g0=1, g 1 = 0 g_1 = 0 g1=0, g 2 = 1 g_2 = 1 g2=1, g 3 = 1 g_3 = 1 g3=1。
请注意,无论是何种LFSR, g 0 g_0 g0 与 g n g_n gn都是不可能为0的。
我们可以写出这样一段C语言代码描述这个3位的LFSR
void lfsr3()
{
unsigned int temp0, temp1, temp2;
temp0 = ff0; //拷贝ff0
temp1 = ff1; //拷贝ff1
temp2 = ff2; //拷贝ff2
ff0 = temp2;
ff1 = temp0 ^ (0 * temp2);
ff2 = temp1 ^ (1 * temp2);
}
现在我们令三个ff的初值为 f f 0 = 1 ff_0 = 1 ff0=1、 f f 1 = 0 ff_1 = 0 ff1=0、 f f 2 = 0 ff_2 = 0 ff2=0,运行这段代码20次可以得到如下结果:
// ff2 ff1 ff0
[1]: 0 0 1
[2]: 0 1 0
[3]: 1 0 0
[4]: 1 0 1
[5]: 1 1 1
[6]: 0 1 1
[7]: 1 1 0
[8]: 0 0 1
[9]: 0 1 0
[10]: 1 0 0
[11]: 1 0 1
[12]: 1 1 1
[13]: 0 1 1
[14]: 1 1 0
[15]: 0 0 1
[16]: 0 1 0
[17]: 1 0 0
[18]: 1 0 1
[19]: 1 1 1
[20]: 0 1 1
很明显可以看到每7次一个循环,我们看到这个LFSR恰好达到了最多的状态数。至于为什么且看下面的分析。
LFSR的行为
LFSR的行为是比较难于分析的。事实上这是一个伽罗华域(Galois Field)上的除法运算。这里同样以上面的那个3位的LFSR为例。
图中的3位数按照从高到低的顺序,即( f f 2 , f f 1 , f f 0 ff_2 ,ff_1 ,ff_0 ff2,ff1,ff0)的顺序。
100 = ( 1 × x 0 ) + ( 0 × x 1 ) + ( 0 × x 2 ) = x 0 100 = (1\times x^0)+(0\times x^1)+(0\times x^2)=x^0 100=(1×x0)+(0×x1)+(0×x2)=x0
于是这个状态转移图可以描述为一个多项式结果的转换,特别地,这里x=2

这样做有什么意义呢?
前面说到,这样一个LFSR的行为可以视作一个伽罗华域的除法。对于伽罗华域而言,其四则运算封闭,则结果必然是这个域中的一个元素。这个域我们记作 G F ( 2 3 ) GF(2^3) GF(23)。

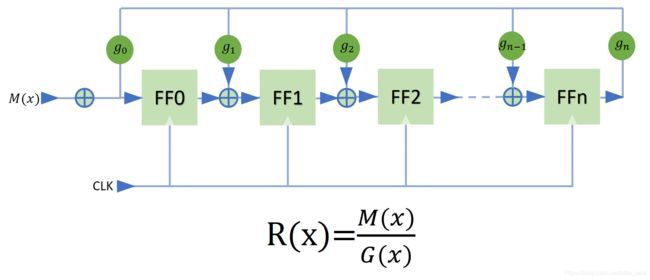
这里 R ( x ) R(x) R(x)是ff的值, M ( x ) M(x) M(x)是输入多项式, G ( x ) G(x) G(x)是抽头多项式。
注意这个是在伽罗华域中的除法运算,本质上是一个模二除法。
这里给出 M ( x ) M(x) M(x)的值,列出下表(当 G ( x ) = x 3 + x 2 + x 0 G(x)=x^3+x^2+x^0 G(x)=x3+x2+x0时)
| M ( x ) M(x) M(x) | R ( x ) R(x) R(x) |
|---|---|
| x 0 x^0 x0 | x 0 x^0 x0 |
| x 1 x^1 x1 | x 1 x^1 x1 |
| x 2 x^2 x2 | x 2 x^2 x2 |
| x 3 x^3 x3 | x 2 + x 0 x^2+x^0 x2+x0 |
| x 4 x^4 x4 | x 2 + x 1 + x 0 x^2+x^1+x^0 x2+x1+x0 |
| x 5 x^5 x5 | x 1 + x 0 x^1+x^0 x1+x0 |
| x 6 x^6 x6 | x 2 + x 1 x^2+x^1 x2+x1 |
对照上面的状态转移图,我们可以看到实际上这个LFSR的行为就是一个模二除法的输出,除法表达式受抽头表达式的控制。
对于一个 n n n位的LFSR,可用的抽头至少有 n n n个(第0个抽头是必须的,不算数)
虽然一个 n n n位的LFSR可以有很多种不同的抽头配置,但不是所有抽头都能使其达到最长输出序列。下表给出一些能够使LFSR达到最长反馈的抽头配置
| LFSR位数 | 状态周期 | 抽头配置 | LFSR位数 | 状态周期 | 抽头配置 |
|---|---|---|---|---|---|
| 2 | 3 | 2,1 | 17 | 131,071 | 17, 14 |
| 3 | 7 | 3, 2 | 18 | 262,143 | 18, 11 |
| 4 | 15 | 4, 3 | 19 | 524, 287 | 19, 6, 2, 1, |
| 5 | 31 | 5, 3 | 20 | 1,048,575 | 20, 17 |
| 6 | 63 | 6, 5 | 21 | 2,097,151 | 21, 19 |
| 7 | 127 | 7, 6 | 22 | 4,194,303 | 22, 21 |
| 8 | 255 | 8, 6, 5, 4, | 23 | 8,388,607 | 23, 18 |
| 9 | 511 | 9, 5 | 24 | 16,777,215 | 24, 23, 22, 17, |
| 10 | 1,023 | 10, 7 | 25 | 33,554,431 | 25, 22 |
| 11 | 2,047 | 11, 9 | 26 | 67,108,963 | 26, 6, 2, 1, |
| 12 | 4,095 | 12, 6, 4, 1, | 27 | 134,217,727 | 27, 5, 2, 1, |
| 13 | 8,191 | 13, 4, 3, 1, | 28 | 268,435,455 | 28, 25 |
| 14 | 16,383 | 14, 5, 3, 1, | 29 | 536,870,911 | 29, 27 |
| 15 | 32,767 | 15, 14 | 30 | 1,073,741,823 | 30, 6, 4, 1, |
| 16 | 65,535 | 16, 15, 13, 4, | 31 | 2,147,483,646 | 31, 28 |
| 32 | 4,294,967,294 | 32, 22, 2, 1, |
这里抽头对应的多项式 G ( x ) G(x) G(x)均为 G F ( 2 n ) GF(2^n) GF(2n)域上的本原多项式。
需要注意的是一个确定域上的本原多项式可能不止一个,例如 G F ( 2 3 ) GF(2^3) GF(23)上的本原多项式除了 x 3 + x + 1 x^3+x+1 x3+x+1还有 x 3 + x 2 + 1 x^3+x^2+1 x3+x2+1,这个大家可以验证以下,这俩多项式构造的LFSR序列长度都是7。
本原多项式可以通过查表获得,也可以通过特定算法生成,这些生成算法在某些领域非常有用。
LFSR应用
PRBS(随机序列)发生器
在通信系统经常会用到一些PRBS,这些发生器可以使用一定长度的LFSR构建。由上面的结论可知,当抽头表达式恰好为本原多项式时,LFSR由最长PRBS输出。即使抽头表达式不为本原多项式,足够位数的LFSR产生的PRBS长度依然非常可观!
我们可以使用一些经典的分立器件构造LFSR,例如D触发器74HC574。
需要注意的是,如果使用移位寄存器构造LFSR,则要使用斐波那契型的LFSR。
值得关注的是Fibonacci型提高工作频率的时候容易出现误码(可以观察反馈抽头和移位寄存器),因此Galois型设计可以有更高的码率。
利用HDL在CPLD或FPGA上实现LFSR也是非常方便的。

这个就是一个32位的LFSR,抽头表达式为 x 32 + x 22 + x 2 + x + 1 x^{32 }+ x^ {22} + x^ 2 + x + 1 x32+x22+x2+x+1,是一个本原多项式。
白噪声发生器
白噪声是在其频率范围内频谱平坦的噪声,功率谱密度和每单位带宽的功率在噪声带宽上是恒定的。
假若将PRBS发生器输出接入一个权电阻网络,就可以构成一个速度还不错的DAC,DAC的输出经过低通滤波,可以在一定带宽内得到不错的白噪声。
补充:另外几种低成本的白噪声产生方法
1.利用电阻的约翰逊噪声产生白噪声
这个方法比较简单,噪声电压密度为
V N O I S E = 4 k B T R V_{NOISE} = \sqrt{4k_{B}TR} VNOISE=4kBTR
其中 k B k_B kB为玻尔兹曼常数。
2.利用PN结的齐纳击穿
可以使用二极管或者BJT或者JFET有PN结的东西产生白噪声,这个容易在版图上实现。目前intel CPU内部的真随机数发生器是这个原理。
PRBS设计白噪声发生器的缺点
滤波器难以设计
带宽受限
CRC计算
CRC计算实际是一个 G F ( 2 n ) GF(2^n) GF(2n)上的除法,又叫做模二除法。加入能够注意到这幅图,CRC的计算就迎刃而解。

CRC多项式对应了 G ( x ) G(x) G(x),现在只需要依次输入 M ( x ) M(x) M(x)即可,微调以下LFSR的结构,加一个异或门,变成这个亚子
RS编码
这个目前博主没有研究,留一个坑等以后填。