求最大子序列和问题（读《数据结构与算法分析——C语言描述》有感）

大四下学期买了一本《数据结构与算法分析—C语言描述》，由于当时也快毕业了，哪还有学习的心思啊，所以看了几页就没耐心了，它就被束之高阁了。幸好，毕业时没把它当废书处理了而是把它带到了工作的地方，时隔两年，再次翻阅，甚是后悔啊，后悔“为什么当时没能读下去”。

开篇就有一个选择问题“设有一组N个数而要确定其中第k个最大者”。

针对这个问题，相信很多人都会想到以下思路：将这N个数读进一个数组中，再通过某种简单的算法，比较冒泡排序法，以递减顺序将数组排好序，然后返回位置k上的元素。

比这个稍微好点的算法是：先把前k个元素读入数组（以递减的顺序）对其排序，然后接剩下的元素再逐个读入，当新元素被读到时，如果它小于数组中的第k个元素则忽略，否则就将其放到数组中正确的位置上，同时将数组中的一个元素挤出数组。当算法终止时，位于第k个位置上的元素作为答案返回。

这两种算法的编码都还不复杂，但是我们会问：哪个算法更好？哪个算法更重要？还是两个算法足够好。使用含有一百万个元素的随机文件，在k=500000的条件下进行模拟发现，每种算法都需要计算机处理若干天才能计算完（我并没有模拟，这是作者的说明），这显然不是我们想要的结果。当然，在此问题中，空间复杂度显得不是那么重要了。但是，时间复杂度却异常重要。当我们分析时间复杂度时，我们需要的是最坏情况下的运行时间。这有两方面的原因：其一，它 对所有的输入提供了一个界限，包括特别坏的输入，而平均情况分析不提供这样的界限；其二，平均情况的界计算起来通常要困难得多。

最大的子序列和问题：给定整数A_1,A₂,…,A_N(可能有负数)，求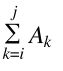的最大值（为了方便起见，如果所有整数均为负数，则最大子序列和为0）。

例如，输入 -2，11，-4，13，-5，-2时，答案为20（从A₂到A₄）。

这个问题之所以有吸引力，是因为求解它有很多解法，而不同解法的时间复杂度又相差甚远！

穷举法：这是最容易想到的一种方法，即把所有的子序列的和都列举出来，一比便知结果。

该算法的正确性不容置疑，运行时间为O(N³)，这完全取决于第22和23行，第23行由一个含于三重嵌套for循环中的O(1)语句组成。第18行上的循环大小为N。

第2个循环大小为N - i，它可能要小，但也可能是N。我们必须假设最坏的情况，而这可能会使的最终的界有些大。

第3个循环的大小为j - i + 1，我们也假设它的大小为N。

因此，总数为O(1*N*N*N) = O(N³)。所以，我们可以简单地认为它的算法复杂度为N³。 

通过观察我们发现，第22和23行上的计算过分地耗时了。我们对它进行优化后： 

大体思路为：以数组[-2,11,-4,13,-5,-2]为例，先从元素-2开始向右找，计算这一轮可能的最大子序列的和；再从元素11向右找，计算此轮可能的最大子序列的和，依次类推。

对这个问题还有一个递归和相对复杂的O(N logN)解法，如果没出现O(N)（线性的）解法，这个算法就会是体现递归威力的极好的范例了。该方法采用的是一种“分治”策略。其想法是：把问题分成两个大致相等的子问题，然后递归地对他们求解，这是“分”部分；“治”阶段将两个子问题的解合并到一起并可能再做些少量的附加工作，最后得到整个问题的解。

在我们的问题中，最大子序列的和可能在三处出现：

1.出现在输入数据的左半部分

2.出现在输入数据的右半部分

3.跨越输入数据的中间从而占据左右两部分

针对1、2两种情况，可以递归求解

情况3的最大和可以通过求出前半部分的最大和（包含前半部分的最后一个元素）以及后半部分的最大和（包含后半部分的第一个元素）而得到，然后将这两个和加在一起。

比如，以下输入：4 ，-3 ，5 ，-2 ，-1 ，2 ， 6， -2。其中前半部分的最大子序列之和为6（从第1个元素到第3个元素），而后半部分的最大子序列和为8（从第6个元素到第7个元素）。

前半部分包含最后一个元素的最大和是4（从第1个元素到第4个元素），而后半部分包含其第一个元素的最大和是7（从第5个元素到第7个元素）。因此横跨这两部分且通过中间的最大和为4 + 7 = 11。代码实现为：

从第79到第85行处理基准情况。如果left == right，那么只有一个元素，并且当该元素非负时它就是最大和子序列。left > right的情况是不可能出现的。第89和90行执行两次递归调用。我们可以看到，递归调用总是对小于原问题的问题进行。

第92到99行计算到达中间边界的左半部分的最大和数，第101到108行计算到达中间边界的右半部分的最大和数。然后，这两个最大和的和为扩展到左右两边的最大和。Max3函数返回这三个可能的最大和中的最大者。

计算时间复杂度：

令T(N)为求解大小为N的最大子序列和问题所花费的时间。如果N=1,则第79到85行花费某个时间常量，我们称之为一个时间单元。于是T(1) = 1。否则，程序必须进行两次递归调用，在第94到108行花费的时间为O(N)。除了第89和90行之外的代码的工作量为常量，从而与O(N)相比可以忽略。

其余就是这两个递归调用的工作了。这两行求解大小为N/2的子序列问题（假设N是偶数）。因此，这两行每行花费T(N/2)个时间单元，共花费2T(N/2)个时间单元。所以，我们为此算法花费的时间得到方程组：

T(1) = 1

T(N) = 2T(N/2) + O(N)

为了简化计算，我们用N代替O(N)。根据此递归方程，我们可以得到：

T(2) = 4 = 2 * 2

T(4) = 12 = 4 * 3

T(8) = 32 = 8 * 4

T(16) = 80 = 16 * 5

所以，我们可以得到通用形式：T(N) = N * (k + 1) = N logN + N = O(N logN) (其中，若N=2^k)。所以，此递归算法的时间复杂度为O(N logN)。

此外，第四种算法为：

很明显，此算法的时间复杂度为O(N)。

该算法的一个附带优点是：它只对数据进行一次扫描，一旦A[i]被读入并处理，它就不再被记忆。因此，如果数组在磁盘上，它就可以被顺序读入，在主存中不必存储数组的任何部分。

说到这，我对此书的看法就是：相见恨晚哪！！！

惭愧，惭愧。