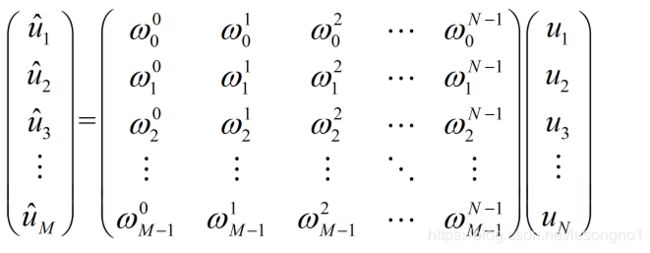FFT的并行实现
关键词:快速傅里叶变换 高维FFT 并行计算
快速傅里叶变换简介
离散傅里叶变换
离散傅里叶变换(DFT)一般定义为: F n ≡ ∑ k = 0 N − 1 f k e − 2 π i n k / N F_n \equiv \sum_{k=0}^{N-1}f_ke^{-2\pi ink/N} Fn≡k=0∑N−1fke−2πink/N
离散傅里叶逆变换可以定义为: f k = 1 N ∑ k = 0 N − 1 F n e − 2 π i n k / N f_k = \frac{1}{N} \sum_{k=0}^{N-1}F_ne^{-2\pi ink/N} fk=N1k=0∑N−1Fne−2πink/N
这里 e e e头上的符号不管放在正变换那还是负变换那里都是没有关系的。正负变换前面的系数是什么也都不打紧,只要乘积为 1 N \frac{1}{N} N1即可。
按矩阵呈向量的观点来看,简单地说,DFT就是把一个 N N N长的向量,通过乘以一个 M × N M \times N M×N的矩阵,变成 M M M长的向量(一般情况下 M = N M=N M=N)。重要的是,这个变换矩阵是什么呢?其实它是一个范德蒙德矩阵,所以DFT其实就可以写为如图所示。
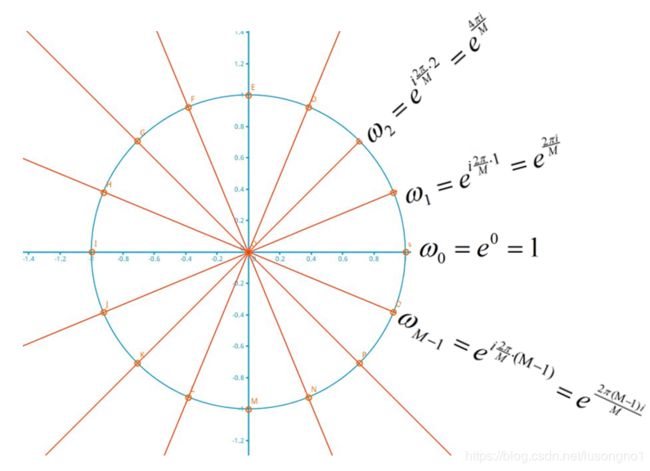
那么这个 ω 0 , ω 1 . . . ω M − 1 \omega_0,\omega_1...\omega_{M-1} ω0,ω1...ωM−1是个什么玩意儿呢?它其实就是复单位圆周上的M个等分点位置。如图所示。
一言以蔽之,要将一个N长的向量变成M长的向量,将复平面的上单元圆分成M分,取第1个等分点,乘方出来N个数,和原来的N长向量做內积,得到傅里叶变换出来的第1个数,依次类推,每个等分点都能出来一个数,那么M个等分点就能出来M个数。
我想到这,我应该把离散傅里叶变换将清楚了。非要用公式来表达的话,同前所写,不过我这里用了不同的符号,如下:
u ^ k = ∑ j = 0 N − 1 e i 2 π k M ⋅ j ⋅ u j , j = 1 , 2 , . . . , N \hat u_k = \sum\limits_{j=0}^{N-1}{e^{i\frac{2\pi k}{M}\cdot j}\cdot u_j},j=1,2,...,N u^k=j=0∑N−1eiM2πk⋅j⋅uj,j=1,2,...,N
上面提到的都是一维的傅里叶变换,二维傅里叶变换其实就是在两个维度上分别做傅里叶变换。
快速傅里叶变换
在实际计算中,人们不直接采用上述离散傅里叶变换的定义式进行计算,而是使用快速傅里叶变换(Fast Fourier Transform),我们可以简单地先把快速傅里叶变换认为是一种做离散傅里叶变换的快速算法。
快速傅里叶变换被誉为二十世纪最伟大的算法之一。所谓的快速傅里叶变换(Fast Fourier Transform,简称FFT),不过是求解离散傅里叶变换的一个快速算法。它将原本计算量为 O ( N 2 ) O(N^2) O(N2)的DFT求和公式,降为了 O ( N log N ) O(N \text{log} N) O(NlogN)。
但是,为了获得较高的运算速度,待变换序列的元素数量必须是 2 n 2^n 2n形式个。
由上述可知,所谓的DFT,不过是一个以输入向量为系数的多项式,在复单位圆周上取不同等分点得到的值。即寻求 ω i , i = 0 , 1 , 2 , . . . , n − 1 \omega_i,i=0,1,2,...,n-1 ωi,i=0,1,2,...,n−1在如下多项式上的取值:
p ( x ) = a 0 + a 1 ( x ) + ⋯ + a n − 1 x n − 1 p(x) = a_0 + a_1(x)+\dots+a_{n-1}x^{n-1} p(x)=a0+a1(x)+⋯+an−1xn−1
那么FFT的精髓就可以写为如下三步:
-
将多项式按奇偶分为两部分, p ( x ) = p 2 ( x 2 ) + x p 1 ( x 2 ) p(x) = p_2(x^2)+xp_1(x^2) p(x)=p2(x2)+xp1(x2),这里
p 2 ( x ) = a 0 + a 2 ( x ) + a 4 ( x 2 ) + … a n − 2 x n / 2 − 1 p 1 ( x ) = a 1 + a 3 x + a 5 x 2 + ⋯ + a n − 1 x n / 2 − 1 \begin{aligned} p_2(x) &=& a_0 + a_2(x) + a_4(x^2)+\dots a_{n-2}x^{n/2-1} \\ p_1(x) &=& a_1 + a_3x + a_5x^2+\dots + a_{n-1}x^{n/2-1} \end{aligned} p2(x)p1(x)==a0+a2(x)+a4(x2)+…an−2xn/2−1a1+a3x+a5x2+⋯+an−1xn/2−1 -
从上所述,那么,问题就变为了求点 ( ω 0 ) 2 , ( ω 1 ) 2 … ( ω n − 1 ) 2 (\omega_0)^2,(\omega_1)^2\dots(\omega_{n-1})^2 (ω0)2,(ω1)2…(ωn−1)2在 p 1 ( x ) p_1(x) p1(x)
和 p 2 ( x ) p_2(x) p2(x)上的取值。容易看到求 ( ω 0 ) 2 , ( ω 1 ) 2 … ( ω n / 2 − 1 ) 2 (\omega_0)^2,(\omega_1)^2\dots(\omega_{n/2-1})^2 (ω0)2,(ω1)2…(ωn/2−1)2
(即 ( ω n / 2 + 1 ) 2 , ( ω n / 2 + 2 ) 2 … ( ω n − 1 ) 2 (\omega_{n/2+1})^2,(\omega_{n/2+2})^2\dots(\omega_{n-1})^2 (ωn/2+1)2,(ωn/2+2)2…(ωn−1)2)是两个规模减半的傅里叶变换。求得规模减半的福利变换,根据上述的 p ( x ) p(x) p(x)和 p 1 ( x ) p_1(x) p1(x)和 p 2 ( x ) p_2(x) p2(x)的关系,可求得原来的傅里叶变换。 -
求 p 1 ( x ) , p 2 ( x ) p_1(x),p_2(x) p1(x),p2(x)的傅里叶变换,又可以拆成规模更小的傅里叶变换,如此层层向下,直到单值的傅里叶变换为其本身。
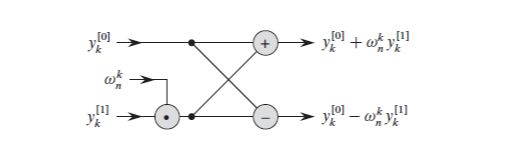
如上所述,FFT是可以递归实现的,写成伪代码,如图所示。另外,在计算 p ( x ) p(x) p(x)的值时,可以利用到 e i θ = − e i ( π + θ ) e^{i\theta }= - e^{i(\pi+\theta)} eiθ=−ei(π+θ)的性质,进一步减少重复的计算。如图[FFTS]所示。
写一个简单的cpp脚本如下:
#include
#include
#define _USE_MATH_DEFINES//pi使用M_PI表示
#include
/*fft的一个串行实现,因为c中没有复数(在有的标准下有,但是使用方法不尽相同,还不如自己写一个),
所以我们需要定义复数及其运算,使用结构体。*/
typedef struct Complex
{
double r=0.0;//初始值设置为0
double i=0.0;//初始值设置为0
} complex;
/**
函数,复数加和减
**/
void complex_add(complex* result, const complex *c1, const complex *c2)
{
result->i = c1->i + c2->i;
result->r = c1->r + c2->r;
}
void complex_sub(complex* result, const complex *c1, const complex *c2)
{
result->i = c1->i - c2->i;
result->r = c1->r - c2->r;
}
/**
函数,复数乘
**/
void complex_multiply(complex* result, const complex *c1, const complex *c2)
{
(result->i) = (c1->r)*(c2->i) + (c1->i)*(c2->r);
(result->r) = (c1->r)*(c2->r) - (c1->i)*(c2->i);
}
/**
函数,复数赋值
**/
void complex_copy(complex* result, const complex *c1)
{
result->r = c1->r;
result->i = c1->i;
}
/**
定义一个求数组长度的运算,包括结构体数组, 尽量少用指针,容易出错
**/
int length(complex a[])
{
int length = sizeof(a) / sizeof(a[0]);
return length;
}
void fft(complex a[],complex y[],int n)//因为不能返回数组,所以只能这么干
{
//int n = length(a);
// printf("%f", length(a));
// printf("%f", a[2].r);
// getchar();
if (n == 1)
{
//A = a;//不知道这样写行不行,先放着
complex_copy(y, a);
return;
}
complex omega_n;
// printf("%f", M_PI);
omega_n.r = cos(2 * M_PI / n);
omega_n.i = sin(2 * M_PI / n);
complex omega;
omega.r = 1;
int half_n = int(n*0.5);
complex* a1 = (complex*)malloc(sizeof(complex)*half_n);
complex* a2 = (complex*)malloc(sizeof(complex)*half_n);
//complex a1[half_n];
for (int i = 0; i < half_n; i++)
{
complex_copy(&a2[i], &a[i * 2]);
complex_copy(&a1[i], &a[i * 2+1]);//分成奇数和偶数
// a2(i) = a(i * 2);
// a1(i) = a(i * 2 + 1);
}
//complex y2[1];
//complex y1[];
complex* y1 = (complex*)malloc(sizeof(complex)*half_n);
complex* y2 = (complex*)malloc(sizeof(complex)*half_n);
fft(a2,y2,int(n*0.5));
fft(a1,y1,int(n*0.5));
// double complex y[n];
// complex* const y = (complex*)malloc(sizeof(complex)*n);
// complex omega_n;
// complex omega;
for (int k = 0; k <= half_n - 1; k++)
{
complex t;
// t->r = 0;
// t->i = 0;
complex_multiply(&t, &omega, &y1[k]);
// complex *t = complex_multiply(&omega, &y1(k));
complex_add(&y[k], &y2[k],&t);
// y(k) = y2(k) + t;
complex_sub(&y[k + half_n], &y2[k], &t);
// y(k + half_n) = y2(k) - t;
// omega = omega*omega_n;
complex omega_temp = omega;
complex_multiply(&omega, &omega_temp, &omega_n);
}
//return y;
}
void main()
{
complex a[4];
complex A[4];
a[0].r = 1;
a[1].r = 2;
a[2].r = 3;
a[3].r = 4;
fft(a,A,4);
printf("result is\n");
for (int i = 0; i < 4; i++)
{
printf("%f+%fi\n", A[i].r, A[i].i);
}
//for (int i = 0; i < length(a); i++)
//{
// printf('test');
//}
// c(1,1);
// _C_double_complex a;
// a = 2I;
// double m = exp(0.1*I);
// printf("%f", m);
getchar();
}
如果写成matlab的脚本为:
function y = myfft( a )
%UNTITLED2 此处显示有关此函数的摘要
% 此处显示详细说明
n = length(a);
if n==1
y = a;
return;
end
wn = exp(2*pi*i/n);
w = 1;
a2 = a([1:2:n]);
a1 = a([2:2:n]);
y2 = myfft(a2);
y1 = myfft(a1);
for k=1:n/2
t = w*y1(k);
y(k)=y2(k)+t;
y(k+n/2) = y2(k)-t;
w = w*wn;
end
end
上述为傅里叶变换的递归实现,为了实现并行,我们其实可以将其写为一种迭代(循环)实现。什么叫迭代实现呢?考虑上述递归的FFT,以8点DFT为例,其递归划分过程如图所示。这里因不是本文重点,故不再细述。
要对序列[0 7]{}做一个DFT,根据FFT原理,只需对[0,2,4,6]{}以及[1,3,5,7]{}做DFT。继续划分,则需对[0,4]{}[2,6]{}[1,5]{}[3,7]{}做DFT。最后是对0,4,2,6,1,5,3,7分别作单点DFT。所以,只要我们知道最底层的数字的排序方式,完全可以逐层从下到上开始计算,知道第一层,不需要递归。事实上,我们可以发现,源序列04261537的二进制数分别是000,100, 010, 110, 001, 101, 011, 111,每个数倒置一下得到000, 001, 010, 011,100, 101, 110,111,正好就是01234567。对于其他2的幂也是成立的。那么,就可据此将递归步,通过几层循环来实现,有人将以此设计出来的非递归算法称为“蝶形”(butterfly)迭代算法。如图所示。
离散傅里叶变换的并行分解
并行化策略
我们可以将规模为 N N N的傅里叶变换分解成相互独立的规模更小的傅里叶变换以便于并行实现,分解也使得内存管理变得更加灵活。一个简单的想法就是将输入向量看成一个二维的向量( m × M m \times M m×M),这里, N , m , M N,m,M N,m,M都是2的指数次方量级的。那么, f f f的各个成分就可以表示为: f [ J m + j ] , 0 ≤ j < m , 0 ≤ J < M f[Jm+j],0\leq j<m, 0\leq J<M f[Jm+j],0≤j<m,0≤J<M
可以看到,这里的 j j j指标变得更快,而 J J J指标变得更慢。用中括号括起来的是向量的下标,下标从 0 0 0开始。
那么,原来的离散傅里叶变换就可以写为: ( l a b e l 2.6 ) F [ k M + K ] = ∑ j , J e 2 π ( k M + K ) i M m ( J m + j ) f ( J m + j ) , 0 ≤ k < m , 0 ≤ K < M (label{2.6}) F[kM+K] = \sum_{j,J} e^{\frac{2\pi(kM+K)i}{Mm}(Jm+j)}f(Jm+j),0\leq k<m,0\leq K<M (label2.6)F[kM+K]=j,J∑eMm2π(kM+K)i(Jm+j)f(Jm+j),0≤k<m,0≤K<M
这里的 k k k和 K K K决定了结果的下标。 F F F中 K K K变化得更快一些。从方程([2.6])中,我们可以做一个恒等的变换,得到:
( l a b e l 2.7 ) F [ k M + K ] = ∑ j { e 2 π i j k / m [ e 2 π i j K / ( M m ) ( ∑ J e 2 π i J K / M f ( J m + j ) ) ] } (label{2.7}) F[kM+K]=\sum_{j}\{e^{2\pi ijk/m} [e^{2\pi ijK/(Mm)} (\sum_{J}e^{2\pi iJK/M}f(Jm+j)) ]\} (label2.7)F[kM+K]=j∑{e2πijk/m[e2πijK/(Mm)(J∑e2πiJK/Mf(Jm+j))]}
从这里发现,解读这个分解,我们们可以得到如下的并行实现的步骤:
-
固定每个 j j j,从每一个规模为 m m m的小块中,都可以取出一个值,形成一个向量。
-
我们可以对上述的每一个向量做FFT。当然,做FFT之前的 J J J指标,就变成了做FFT
之后的 K K K 指标。 -
给每个组份乘上一个 e 2 π i j K / ( M m ) e^{2\pi ijK/(Mm)} e2πijK/(Mm)。
-
重排数据,使得它们是一组中是以 j ( 0 ≤ j < m ) j(0\leq j<m) j(0≤j<m)为指标变动的向量。
-
对这些向量组在并行的条件下做FFT。那么这时候 j j j指标就变成了 k k k指标。
-
此时就可得到结果以 F [ k M + K ] F[kM+K] F[kM+K]的形式呈现,再做一个反操作,就可以得到我们想要的正确顺序(就是 k k k
变动最快那个顺序))的一个结果。
通过上述,我们虽然把一个FFT操作拆成了两个FFT操作,但是对于每个FFT的计算量上的一个计算方式是不变的:第一步FFT的计算量为 N log M N \text{log} M NlogM,第二部FFT的计算量为 N log m N \text{log} m Nlogm,所以呢,总的计算量为 N log ( M n ) = N log N N \text{log}(Mn)=N \text{log} N Nlog(Mn)=NlogN是没变的。 上述的分解,被称为“zoom transforms”,而上述的FFT的并行方式,在论文中,被叫做是“six-step framework”。
需要注意的话,我这里做的算法有一些假设条件,比如说要求数据长度除以处理机个数的值为2的正整数次方。这样就要求处理的问题规模必须是偶数,最好是2指数次方。
写成的串行c代码如下:
#include
#include
#include
#include
#define N 8192
typedef struct {
double real;
double imag;
} Complex;
Complex Input[N];
Complex Result[N];
Complex Euler[N/2];
void computeEulers()
{
int x = 0;
float theta;
float n = (4.0*M_PI)/N;
for(x = 0; x < (N>>1); x++){
theta = x*n;
Euler[x].real = cos(theta);
Euler[x].imag = -sin(theta);
}
}
Complex multiply(Complex* a, Complex* b)
{
Complex c;
c.real = (a->real * b->real) - (a->imag * b->imag);
c.imag = (a->real * b->imag) + (b->real * a->imag);
return c;
}
Complex add(Complex* a, Complex* b)
{
Complex c;
c.real = a->real+b->real;
c.imag = a->imag+b->imag;
return c;
}
int main(int argc, char** argv)
{
//***************************************************************************
//输入向量赋值,也可以从文件读入
//***************************************************************************
int NN = N;
NN = N;int i;
for(i=0;i>1); k++)
{
even.real = even.imag = odd.real = odd.imag = 0.0;
diff = (k - 1 +(N>>1)) % (N>>1);
idx = 0;
for(n = 0; n < (N>>1); n++){
euler = Euler[idx];
temp = multiply(&Input[n<<1], &euler);
even = add(&even, &temp);
temp = multiply(&Input[(n<<1) +1], &euler);
odd = add(&odd, &temp);
idx = (idx + diff + 1) % (N>>1);
}
theta = k*PI2_by_N;
twiddle.real = cos(theta);
twiddle.imag = -sin(theta);
temp = multiply(&odd, &twiddle);
Result[k] = add(&even, &temp);
temp.real = -temp.real;
temp.imag = -temp.imag;
Result[k+(N>>1)] = add(&even, &temp);
}
clock_gettime(CLOCK_REALTIME, &now);
double seconds = (double)((now.tv_sec+now.tv_nsec*1e-9) - (double)(tmstart.tv_sec+tmstart.tv_nsec*1e-9));
/* printf("C time: %f seconds\n", seconds);
printf("TOTAL PROCESSED SAMPLES: %d\n", N);
printf("============================================\n");
for(k = 0; k <= 10; k++){
printf("XR[%d]: %.5f \t XI[%d]: %.5f\n", k, Result[k].real, k, Result[k].imag);
printf("============================================\n");
}*/
printf("PROCESS NUMBER : %d\n\n", N);
printf("\n\n\nTIME COST EVALUATED BY C: %e secs\n", seconds);
// printf("TIME COST EVALUATED BY MPI: %e secs\n\n\n", mpiend-mpist);
freopen("outputS", "w", stdout);
for(k = 0; k <= NN-1; k++){
//printf("XR[%d]: %.5f \t XI[%d]: %.5f\n", k, ResultR[k], k, ResultI[k]);
printf("X[%d]: %.5f + %.5f i\n", k, Result[k], Result[k]);
}
}
并行化脚本如下:
//**************************************************************
// 一维FFT的MPI并行程序,采用蝶形迭代算法
//***************************************************************
// 输入的数据的长度(偶数)和所用进程数的比值一定要是2的正指数次方
// 如 W/p = 2,4,8...
// 编译: mpicc FFTParallel.c -lm -o FFTParallel
// 运行:mpiexec mpirun qsub
// 陆嵩
// 最后一次修改时间:2018.12.20 15:08
//*****************************************************************
#include
#include
#include
#include
#include
#define N 8
//***************************************************************************
//定义一个复数的结构
//***************************************************************************
typedef struct {
double real;
double imag;
} Complex;
//***************************************************************************
//定义一个从文件读取数据的函数 ,没写
//***************************************************************************
/*
bool readFromFile()
{
return true;
}
*/
//***************************************************************************
//定义复数的乘法运算
//参输入数: a、b两个指向复数结构体的指针
//返回c,为复数结构体
//***************************************************************************
Complex multiply(Complex* a, Complex* b)
{
Complex c;
c.real = (a->real * b->real) - (a->imag * b->imag);
c.imag = (a->real * b->imag) + (b->real * a->imag);
return c;
}
//***************************************************************************
//定义复数的加法
//参输入数: a、b两个指向复数结构体的指针
//返回c,为复数结构体
//***************************************************************************
Complex add(Complex* a, Complex* b)
{
Complex c;
c.real = a->real+b->real;
c.imag = a->imag+b->imag;
return c;
}
//***************************************************************************
//主函数入口
//***************************************************************************
int main(int argc, char** argv)
{
int size, rank;int NN,i;int k;int n;
Complex Input[N];
MPI_Init(NULL, NULL);//初始化
MPI_Comm_size(MPI_COMM_WORLD, &size);//获取进程数
MPI_Comm_rank(MPI_COMM_WORLD, &rank);//获取进程编号
int localN = (N/2)/size;//每个节点分配的数目
double EulerR[N/2], EulerI[N/2];
double *ResultR = NULL, *ResultI = NULL;
double tempEulerI[localN], tempEulerR[localN];
double tempResultR[localN*2], tempResultI[localN*2];
struct timespec now, tmstart;//定义时间结构体,struct timespec精确到微秒级别
double mpist, mpiend;
//***************************************************************************
//输入向量赋值,也可以从文件读入
//***************************************************************************
NN = N;
for(i=0;i>1)) % (N>>1);
idx = 0;
for(n = 0; n < (N>>1); n++){
euler.real = EulerR[idx];
euler.imag = EulerI[idx];
temp = multiply(&Input[n<<1], &euler);
even = add(&even, &temp);
temp = multiply(&Input[(n<<1) +1], &euler);
odd = add(&odd, &temp);
idx = (idx + diff + 1) % (N>>1);
}
theta = k*PI2_by_N;
twiddle.real = cos(theta);
twiddle.imag = -sin(theta);
temp = multiply(&odd, &twiddle);
result = add(&even, &temp);
tempResultR[x] = result.real;
tempResultI[x] = result.imag;
temp.real = -temp.real;
temp.imag = -temp.imag;
result = add(&even, &temp);
tempResultR[x+localN] = result.real;
tempResultI[x+localN] = result.imag;
}
//通过收集,把结果都收集都进程0上面来
MPI_Gather(tempResultR, localN, MPI_DOUBLE, ResultR, localN, MPI_DOUBLE, 0, MPI_COMM_WORLD);
MPI_Gather(tempResultI, localN, MPI_DOUBLE, ResultI, localN, MPI_DOUBLE, 0, MPI_COMM_WORLD);
MPI_Gather(tempResultR+localN, localN, MPI_DOUBLE, ResultR+(N/2), localN, MPI_DOUBLE, 0, MPI_COMM_WORLD);
MPI_Gather(tempResultI+localN, localN, MPI_DOUBLE, ResultI+(N/2), localN, MPI_DOUBLE, 0, MPI_COMM_WORLD);
if(rank == 0)
{
mpiend = MPI_Wtime();/////////////////////////////////////////////////////////// 计时终点
clock_gettime(CLOCK_REALTIME, &now);///////////////////////////////////////////
double seconds = (double)((now.tv_sec+now.tv_nsec*1e-9) - (double)(tmstart.tv_sec+tmstart.tv_nsec*1e-9));
printf("PROCESS NUMBER : %d\n\n", N);
printf("\n\n\nTIME COST EVALUATED BY C: %e secs\n", seconds);
printf("TIME COST EVALUATED BY MPI: %e secs\n\n\n", mpiend-mpist);
freopen("output", "w", stdout);
for(k = 0; k <= NN-1; k++){
//printf("XR[%d]: %.5f \t XI[%d]: %.5f\n", k, ResultR[k], k, ResultI[k]);
printf("X[%d]: %.5f + %.5f i\n", k, ResultR[k], ResultI[k]);
}
}
MPI_Finalize();
}
高维FFT并行分解
对于二维的FFT变换,只不过是在两个不同的方向,比如书在在 x x x和 y y y方向逐一进行并行的一维FFT变换即可,更高维的情况也是一样。这么干是可以的,但是显得也太蠢了。比如说,在做某个方向的FFT时,把值取出来操作,完了放回去,第二次又将其取出来……这样做无疑增加了不少操作。
所以,在高维情况下做FFT,除了在每个方向都做一次FFT这个蠢办法外,事实上是有一些更高明的方法的。比如基于DSP、FPGA、ARM等的FFT实现等,这里由于篇幅原因,不再赘述,有兴趣的读者可以查看相关文献。
数值实验
计算资源与环境
我用的计算为科学与工程计算国家重点实验室的大规模科学计算四号集群(LSSC-IV)。
它是首次使用纯IntelPurley平台并采用100Gb EDR Infiniband高速网络的千万亿次计算系统。LSSC-IV集群基于联想深腾8810系统构建,包含超算和大数据计算两部分。计算集群主体部分包含408台新一代ThinkSystem SD530模块化刀片(每个刀片包括2 颗主频为2.3GHz 的Intel Xeon Gold 6140 18核Purley处理器和192GB内存),总共拥有14688 个处理器核,理论峰值性能为1081TFlops,实测LINPACK性能703TFlops。系统还包括1台胖结点(Lenovo X3850X6服务器,2颗Intel Xeon E7-8890 V4处理器,4TB 内存,10TB本地存储),4个KNL结点(1颗Intel Xeon Phi KNL 7250处理器,192GB内存)以及管理结点、登陆结点等。
集群系统采用Lenovo DS5760存储系统,磁盘阵列配置双控制器,8GB缓存,主机接口8个16Gbps FC接口,60 块6TB NL_SAS盘作为数据存储,裸容量共计360TB,系统持续读写带宽超过4GB/s,磁盘阵列通过2台I/O结点以GPFS并行文件系统管理,共享输出给计算结点。大数据计算部分包括7 台GPU服务器(分别配置NVIDIA Tesla P40、P100 和 V100计算卡)和由8台Lenovo X3650M5服务器组成的HDFS辅助存储系统。集群系统所有结点同时通过千兆以太网和100Gb EDR Infiniband网络连接。其中千兆以太网用于管理,EDR
Infiniband网络采用星型互联,用于计算通讯。LSSC-IV的操作系统为:Red Hat Enterprise Linux Server 7.3。LSSC-IV 上的编译系统包括Intel C,Fortran编译器,GNU编译器,Intel VTune调试器等。并行环境有MVAPICH2、OpenMPI、Intel MPI,用户可以根据自己的情况选用。LSSC-IV上还安装如下常用数值计算的开源软件:PHG(Parallel Hierarchical Grid),PETSc,Hypre,SLEPc,Trilinos等。用户也可自行在个人目录下安装需要的软件。LSSC-IV采用LSF作业调度系统,两个登陆结点作为任务提交结点。
LSSC-IV系统2017 年11月成功进入全球HPC TOP500排行榜,位列第382位。
并行性能的主要考察指标
加速比:串行执行时间与并行执行时间的比值。
并行效率:加速比与进程数的比值,即 E P = T S P × T P \text {E}_{\text {P}}=\frac {\text {T}_{\text {S}}}{\text {P} \times \text {T}_{\text {P}}} EP=P×TPTS,其中, P \text {P} P为并行程序执行进程数, T P \text {T}_{\text {P}} TP为并行程序执行时间, T S \text {T}_{\text {S}} TS 为串行程序执行时间。
可扩展性:并行效率与问题规模、处理机数量之间的关系。
强可扩展性:保持总体计算规模不变,随着处理器个数的增加,观察并行效率的变化。
弱可扩展性:保持单个节点的计算规模不变,随着处理器个数的增加,观察并行效率的变化。
加速比测试
我们固定核心数为4,改变问题规模,来看看加速比和并行的效率。因为在测量数值比较小时,测量不稳定,我们在程序中计时需要多次计算取平均值。
通过表格,可以观察到看得到,问题规模越大,加速的效果相对就越好。所以说,虽然说问题有其固有的可扩展性限制,可能用到用到没几十个核,加速比就恒定了,但是对于大规模问题来说,因为其加速效率较为可观,其加速效率能够随核心的成倍增长呈现1/2减小,还是很不错的。并行计算很有前景。
强可扩展性测试
固定复向量规模为32768(2e15),依次增加核心数为1、2、4、8、16、32、64、128、256,观察其加速比以及并行效率。因为核心数为1的并行和串行还是不尽相同,所以这里核心数从1开始。
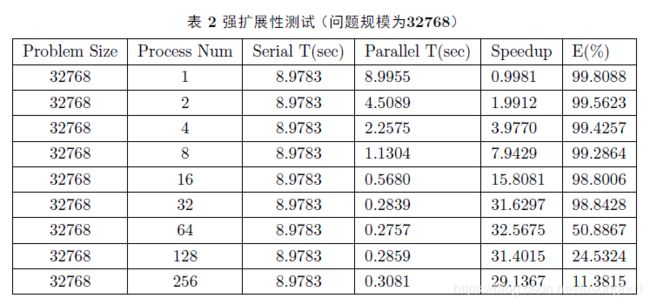
对比两表,可以看得出,问题规模越大,可扩展性越好,也就是说可增加的核心数随问题的规模变大而增加。问题规模越大,可并行性越强。可以观察到并行效率快速下降,可能由每个核的计算粒度的成倍递减造成的。随着核心数的增加,而问题规模不变,通讯开销慢慢占了主导地位。
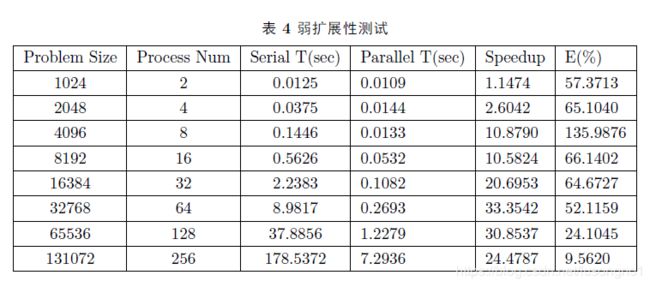
弱可扩展性测试
可以看得出,在问题规模为4096,核心数为8时,获得了最高的并行效率。
总结
本文介绍了一维快速傅里叶变换的并行化实现,并为高维的并行化实现提供了思路。
在并行化方面,基于分解的思想,在并行性能方面,测试了程序的加速比,并行效率以及可扩展性。