POJ2002-Squares
全解题报告索引目录 -> 【北大ACM – POJ试题分类】
转载请注明出处:http://exp-blog.com
-------------------------------------------------------------------------
大致题意:
有一堆平面散点集,任取四个点,求能组成正方形的不同组合方式有多少。
相同的四个点,不同顺序构成的正方形视为同一正方形。
解题思路:
做本题数学功底要很强= =
直接四个点四个点地枚举肯定超时的,不可取。
普遍的做法是:先枚举两个点,通过数学公式得到另外2个点,使得这四个点能够成正方形。然后检查散点集中是否存在计算出来的那两个点,若存在,说明有一个正方形。
但这种做法会使同一个正方形按照不同的顺序被枚举了四次,因此最后的结果要除以4.
已知: (x1,y1) (x2,y2)
则: x3=x1+(y1-y2) y3= y1-(x1-x2)
x4=x2+(y1-y2) y4= y2-(x1-x2)
或
x3=x1-(y1-y2) y3= y1+(x1-x2)
x4=x2-(y1-y2) y4= y2+(x1-x2)
据说是利用全等三角形可以求得上面的公式
有兴趣的同学可以证明下。。。
再来就是利用hash[]标记散点集了
我个人推荐key值使用 平方求余法
即标记点x y时,key = (x^2+y^2)%prime
此时key值的范围为[0, prime-1]
由于我个人的标记需求,我把公式更改为key = (x^2+y^2)%prime+1
使得key取值范围为[1, prime],则hash[]大小为 hash[prime]
其中prime为 小于 最大区域长度(就是散点个数)n的k倍的最大素数,
即小于k*n 的最大素数 (k∈N*)
为了尽量达到key与地址的一一映射,k值至少为1,
当为k==1时,空间利用率最高,但地址冲突也相对较多,由于经常要为解决冲突开放寻址,使得寻找key值耗时O(1)的情况较少
当n太大时,空间利用率很低,但由于key分布很离散,地址冲突也相对较少,使得寻找键值耗时基本为O(1)的情况
提供一组不同k值的测试数据
K==1, prime=997 1704ms
K==2, prime=1999 1438ms
K==8, prime=7993 1110ms
K==10, prime=9973 1063ms
K==30, prime=29989 1000ms
K==50, prime=49999 1016ms
K==100, prime=99991 1000ms
最后解决的地址冲突的方法,这是hash的难点。我使用了 链地址法
typedef class HashTable
{
public:
int x,y; //标记key值对应的x,y
HashTable* next; //当出现地址冲突时,开放寻址
HashTable() //Initial
{
next=0;
}
}Hashtable;
Hashtable* hash[prime]; //注意hash[]是指针数组,存放地址
//hash[]初始化为NULL (C++初始化为0)
先解释所谓的“冲突”
本题对于一组(x,y),通过一个函数hash(x,y),其实就是上面提到的key的计算公式
key = (x^2+y^2)%prime+1
于是我们得到了一个关于x,y的key值,但是我们不能保证key与每一组的(x,y)都一一对应,即可能存在 hash(x1,y1) = hash(x2,y2) = key
处理方法:
(1) 当读入(x1, y1)时,若hash[key]为NULL,我们直接申请一个临时结点Hashtable* temp,记录x1,y1的信息,然后把结点temp的地址存放到hash[key]中
此后我们就可以利用key访问temp的地址,继而得到x1,y1的信息
(2) 当读入(x2, y2)时,由于hash(x1,y1) = hash(x2,y2) = key,即(x2, y2)的信息同样要存入hash[key],但hash[key]已存有一个地址,怎么办?
注意到hash[key]所存放的temp中还有一个成员next,且next==0,由此,我们可以申请一个新结点存放x2,y2的信息,用next指向这个结点
此后我们利用key访问temp的地址时,先检查temp->x和temp->y是否为我们所需求的信息,若不是,检查next是否非空,若next非空,则检查下一结点,直至 next==0
当检查完所有next后仍然找不到所要的信息,说明信息原本就不存在
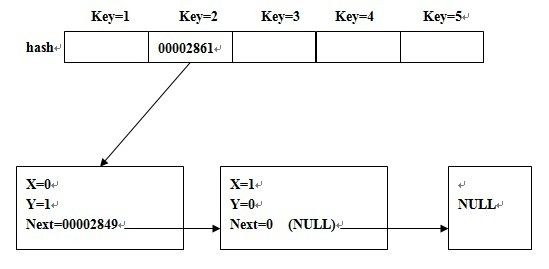
就是说hash[key]只保存第一个值为key的结点的地址,以后若出现相同key值的结点,则用前一个结点的next保存新结点的地址,其实就是一个链表
简单的图示为:
//Memory Time
//652K 1438MS
#include
using namespace std;
const int prime=1999; //长度为2n区间的最大素数 (本题n=1000)
//其他prime可取值:
// 1n 区间: 997 1704ms
// 2n 区间: 1999 1438ms
// 8n 区间: 7993 1110ms
// 10n 区间: 9973 1063ms
// 30n 区间: 29989 1000ms
// 50n 区间: 49999 1016ms
// 100n区间: 99991 1000ms
//为了尽量达到key与地址的一一映射,hash[]至少为1n,
//当为1n时,空间利用率最高,但地址冲突也相对较多,由于经常要为解决冲突开放寻址,使得寻找key值耗时O(1)的情况较少
//当n太大时,空间利用率很低,但由于key分布很离散,地址冲突也相对较少,使得寻找键值耗时基本为O(1)的情况
typedef class
{
public:
int x,y;
}Node;
typedef class HashTable
{
public:
int x,y; //标记key值对应的x,y
HashTable* next; //当出现地址冲突时,开放寻址
HashTable() //Initial
{
next=0;
}
}Hashtable;
Node pos[1001];
Hashtable* hash[prime]; //hash[]是指针数组,存放地址
void insert_vist(int k)
{
int key=((pos[k].x * pos[k].x)+(pos[k].y * pos[k].y))%prime +1; //+1是避免==0
//使key从[0~1998]后移到[1~1999]
if(!hash[key])
{
Hashtable* temp=new Hashtable;
temp->x=pos[k].x;
temp->y=pos[k].y;
hash[key]=temp;
}
else //hash[key]已存地址,地址冲突
{
Hashtable* temp=hash[key];
while(temp->next) //开放寻址,直至next为空
temp=temp->next;
temp->next=new HashTable; //申请新结点,用next指向,记录x、y
temp->next->x=pos[k].x;
temp->next->y=pos[k].y;
}
return;
}
bool find(int x,int y)
{
int key=((x * x)+(y * y))%prime +1;
if(!hash[key]) //key对应的地址不存在
return false;
else
{
Hashtable* temp=hash[key];
while(temp)
{
if(temp->x==x && temp->y==y)
return true;
temp=temp->next;
}
}
return false;
}
int main(void)
{
int n;
while(cin>>n)
{
if(!n)
break;
memset(hash,0,sizeof(hash)); //0 <-> NULL
for(int k=1;k<=n;k++)
{
cin>>pos[k].x>>pos[k].y;
insert_vist(k); //插入哈希表,标记散点
}
int num=0; //正方形的个数
for(int i=1;i<=n-1;i++)
for(int j=i+1;j<=n;j++)
{
int a=pos[j].x-pos[i].x;
int b=pos[j].y-pos[i].y;
int x3=pos[i].x+b;
int y3=pos[i].y-a;
int x4=pos[j].x+b;
int y4=pos[j].y-a;
if(find(x3,y3) && find(x4,y4))
num++;
x3=pos[i].x-b;
y3=pos[i].y+a;
x4=pos[j].x-b;
y4=pos[j].y+a;
if(find(x3,y3) && find(x4,y4))
num++;
}
cout<