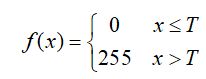数字图像处理（4）—— 图像点运算
目录
1、图像点运算概述
2.点运算的重要工具——灰度直方图
3、图像的变换
3.1、线性变换
3.2、对数变换
3.3 、伽马变换
3.4、灰度阈值变换（二值化）
3.5、分段线性变换
3.6、直方图的均衡化（灰度均衡化）
3.7、直方图规定化
对一个数字图像处理系统来说，一般的处理过程为三个步骤：图像预处理、特征抽取、图像识别和分析。图像的点运算就是预处理过程中的重要一步。
1、图像点运算概述
点运算是指对图像的每个像素依次进行相同的灰度变换，然后得出的图像就是输出图像。那么对于RGB彩色图像的点运算是怎么处理的呢？（这里我放一个我的推测：RGB图像的点运算是对每个通道均进行相同的灰度变换，然后再转化成一个三维矩阵，显示即可。所以我们主要围绕灰度图像进行讲解，RGB图像就是做了三次处理得到的）。
2.点运算的重要工具——灰度直方图
我们最早接触直方图是在统计学中。假设我们现在有一个城市的年龄统计表（这是一个含有几十万人的表格），那么为了直观地看到这个城市的年龄分布情况，我们总不能对着表格一个一个地数吧。这时，采用饼状图、直方图等方式，可以很明显地反映出各个年龄段的人数分布情况。直方图可以用于很多情况，学生的成绩统计、某小区的职业统计等等。而高斯分布就是直方图体现的最令人惊艳的规律。
很多统计会呈现中间高，两边低的高斯分布规律
当然，对于图像来说，也有这样一个操作，我们遍历一幅灰度图像，然后将图像的灰度按 0~255 等间距划分，然后填入对应的位置。如果要计算图像灰度级的概率，则只需要做归一化处理即可。
那么我们又要对 Lena 做点什么了。
对 Lena 图像的各个通道的灰度统计，256个灰度级
对 Lena 各个通道的灰度统计，50个灰度级
那么对于灰度图像来说，统计数据如何呢？
对 Lena 的灰度图像进行统计结果，可以看出之前提到的灰度分布均匀的效果
MATLAB代码：
clear
clc
I = imread('lena.jpg');
I1 = 0.299.*I(:,:,1)+0.587.*I(:,:,2)+0.114.*I(:,:,3); % 转化成灰度图
figure(1)
subplot(1,3,1);
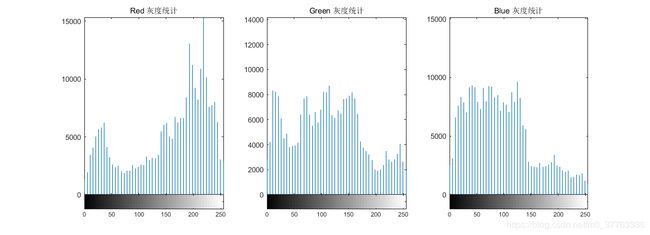
imhist(I(:,:,1),50);
title('Red 灰度统计');
subplot(1,3,2);
imhist(I(:,:,2),50);
title('Green 灰度统计');
subplot(1,3,3);
imhist(I(:,:,3),50);
title('Blue 灰度统计')
% 对灰度图像
figure(2)
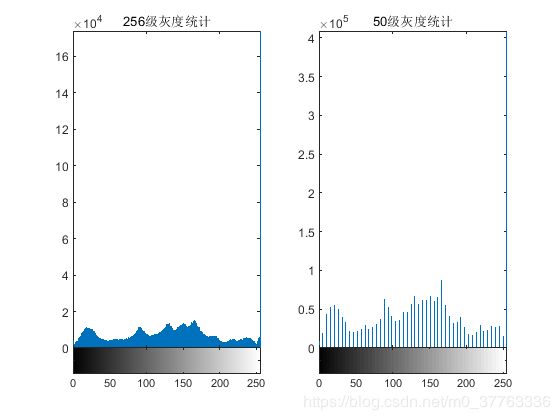
subplot(1,2,1);
imhist(I1);
title('256灰度统计');
subplot(1,2,2);
imhist(I1,50);
title('50灰度统计');
3、图像的变换
3.1、线性变换
线性变换函数是一个一维线性函数，设一维线性变换函数为 f，则有：
其中，fA 是线性函数的斜率，fB为线性函数在y轴的截距；DA 为输入图像像素的灰度，DB表示输出图像的灰度。
线性变换有如下性质：
这里对于MATLAB来说，有一些需要注意的代码细节：
clear
clf
clc
I = imread('lena.jpg');
I1 = 0.299.*I(:,:,1)+0.587.*I(:,:,2)+0.114.*I(:,:,3); % 转化成灰度图
I1 = im2double(I1);
I2 = im2double(I); % 为了对矩阵进行计算，这里需要把数据类型转换为float类型
figure(1)
subplot(1,4,1)
imshow(I); % 原始灰度图像
title('原图像');
% 设线性变换的斜率k，截距b
k = -2;
b = 200;
% 图像的线性变换
I3 = k.*I + b/255;
subplot(1,4,2);
imshow(I3);
title('k=-2,b=200');
k = -0.5;
b = 100;
% 图像的线性变换
I4 = k.*I1+ b/255;
subplot(1,4,3);
imshow(I4);
title('k=-0.5,b=100');
k = -1;
b = 255;
% 图像的线性变换
I5 = k.*I1+b/255;
subplot(1,4,4);
imshow(I5);
title('k=-1,b=255');
（1） fA（斜率）>1时，输出图像的对比度将会增大，fA<1时，输出图像的对比度减小，即线性变换的斜率控制着图像变换后的对比度。
不同k值的情况下对应的输出图像
（2） fA = 1，且 fB != 0时，操作仅是对灰度的上移或下移。其实就是使图像更暗或者更亮。不会对对比度造成影响。
k = 1，b不同的效果
（3）fA < 0时，暗区域会变亮，亮区域会变暗。如果打到饱和，即超出（0~255）范围，则可能丢失细节。如果特殊情况下，，fA == -1, fB == 255，则图像翻转.
可以看出，当k= - 2时，图像整体缺少数据，即像素全部小于0，按0处显示处理
3.2、对数变换
对数变换的表达式如下：
c 为尺度比例常数，s 为源灰度值，t 为变换后的目标灰度。
其实对图像做处理后的对比效果并不是很明显，对数变换的左右主要是对较暗的部分进行增强。其实对数变换主要应用于傅里叶变换领域的分析，那么对于原始图片做傅里叶变换，然后再做对数变换的频谱：
I = imread('lena.jpg');
F = fft2(im2double(I));
F = fftshift(F);
F = abs(F);
T = log(F+1);
subplot(1,2,1);
imshow(F,[]);
title('未变换的频谱');
subplot(1,2,2);
imshow(T,[]);
title('对数变换后的频谱')
3.3 、伽马变换
伽马变换又称指数变换（幂次变换），是一种非线性变换。伽马（gama）指的是指数。表达式如下：
其中， 
为补偿系数，
就是伽马系数，x 为输入图像，y 为输出图像。
不同伽马系数下的伽马曲线情况
这里注意几点：
（1）横纵坐标为什么采用归一化的坐标？
在MATLAB中，图像矩阵的数据类型是 uint，如果想对矩阵进行操作，需要先将其数据类型转换成双精度浮点型，而MATLAB的 im2double 函数是专门用作这个转换的，转后的返回值就是归一化之后的值。
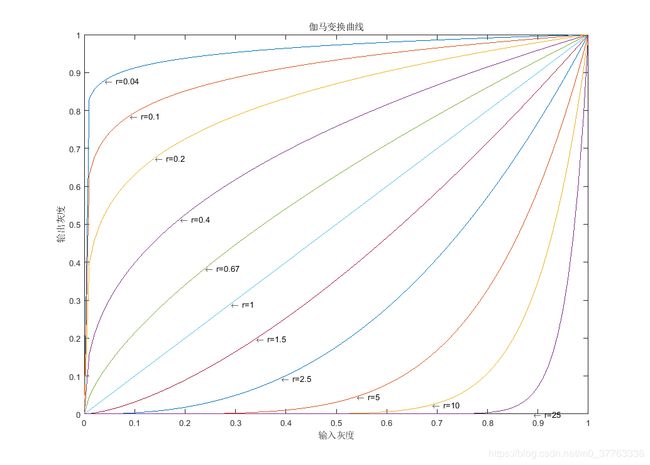
（2）伽马曲线能看出什么？
我们可以看到，对于不同的伽马系数，曲线的形状是不同的，对于 gama == 1这条曲线，我们知道它本质上是一个线性变换。变换为斜率 k = 1，截距 esp 。可以认为是一种特殊的伽马变换。斜率代表了其对比度，即对于斜率大的地方，对比度越高，因此，对于 同一输入灰度，则 gama 选取的不同，相应图像处理后的结果也不同。
从单个伽马系数曲线来看：
gama >1 时，我们可以看到幂函数曲线的斜率是递增的。也就是说，此时对于灰度值高的区域，伽马变换会增加该区域的灰度。
gama < 1时，幂函数曲线的斜率是随灰度增加递减的，那么，如果灰度值越小，且gama 越小，则对于低灰度区域增强效果越大。
由此可知，伽马变换可以增强我们想要增加的灰度区域的灰度，对一些局部区域较暗的图片，我们可以选择较小的 gama 值。
I = imread('lena.jpg');
I1 = 0.299.*I(:,:,1)+0.587.*I(:,:,2)+0.114.*I(:,:,3); % 转化成灰度图
I1 = im2double(I1);
I2 = im2double(I); % 为了对矩阵进行计算，这里需要把数据类型转换为float类型
figure(1)
subplot(2,3,1)
imshow(imadjust(I,[],[],0.75)); % 原始灰度图像
title('gama = 0.75');
subplot(2,3,2);
imshow(imadjust(I,[],[],1));
title('gama = 1');
subplot(2,3,3);
imshow(imadjust(I,[],[],1.5));
title('gama = 1.5');
subplot(2,3,4)
imshow(imadjust(I,[],[],0.1)); % 原始灰度图像
title('gama = 0.1');
subplot(2,3,5);
imshow(imadjust(I,[],[],10));
title('gama = 10');
subplot(2,3,6);
imshow(imadjust(I,[],[],20));
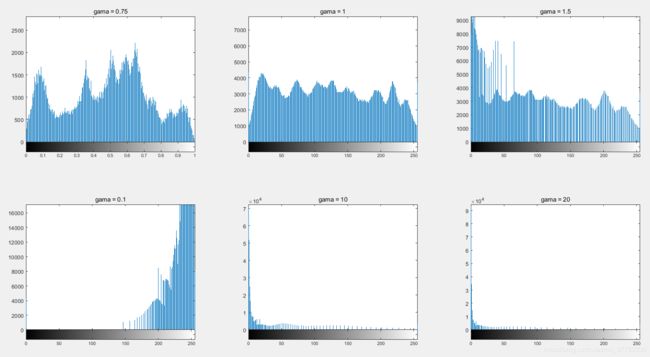
title('gama = 20');那么对于这些伽马系数的直方图又是什么样呢？
伽马系数会改变灰度直方图的分布情况，改变规律和前述一致。
3.4、灰度阈值变换（二值化）
灰度图像的二值化是在很多工作中会用到的方法，对于计算机来说，这种二值化的方法可以有效节省内存，提升计算速度。二值化的最重要的部分就是二值化阈值的选择，这也是称为灰度阈值变换的原因。
数学模型：
T 为阈值，x 为输入的灰度，f(x) 为输出。这个方程的意思就是把小于等于阈值的全部设为黑，大于阈值的设为白。
灰度图像二值化的阈值选取有很多方法，比如OTSU、固定阈值、自适应阈值等。
I = imread('lena.jpg');
I1 = 0.299.*I(:,:,1)+0.587.*I(:,:,2)+0.114.*I(:,:,3); % 转化成灰度图
I1 = im2double(I1);
I2 = im2double(I); % 为了对矩阵进行计算，这里需要把数据类型转换为float类型
thresh = graythresh(I); % 自适应选取阈值
subplot(1,3,1);
imshow(I1);
title('原图像')
bw2 = imbinarize(I1,thresh);
subplot(1,3,2);
imshow(bw2);
title('自适应阈值')
subplot(1,3,3);
bw2 = imbinarize(I1,120/255);
imshow(bw2);
title('自选120为阈值')
不同阈值二值化的效果，看来我运气不错，选了个120作为阈值的效果和自适应差不太多
3.5、分段线性变换
其实理解了前面的内容，这里很简单。对于不同区域的灰度情况，如果采用伽马变换，则会抑制其他区域，所以，分段线性变换就起到既能增强感兴趣区域，又能不造成虽坏其他区域的效果。
3.6、直方图的均衡化（灰度均衡化）
故名思意，其实就是让灰度等级分布的均匀一些，而不是两级或多级分化的情况。均匀的灰度分布，其对比度也强。具体方法可能需要了解一下数学原理了：
目标：给定一幅图像，通过一定的处理，得到对比度强的输出（均衡化的直方图）；
方法：为了便于分析，考虑 0~1 且连续的情况下。此时图像（灰度/直方图）的归一化就是概率分布情况（PDF）。
则概率分布 p 满足：
由概率分布函数的性质可知： 
，即概率总和为1.
设转换前的概率为 
，转换后的概率 
，转化的映射函数为 
,即 
，求导。则：
详细的数学推导看这里：https://blog.csdn.net/timeless_2014/article/details/80389433
其实就是为了将一个未知的分布函数转换成均匀分布。
那么最终得到的灰度均衡转换方程：
那么看看效果，由于 Lena 的灰度分布本来就比较均衡，所以这次用我老婆了。
I = imread('gakki.jpg');
I1 = 0.299.*I(:,:,1)+0.587.*I(:,:,2)+0.114.*I(:,:,3); % 转化成灰度图
I1 = im2double(I1);
I2 = im2double(I); % 为了对矩阵进行计算，这里需要把数据类型转换为float类型
figure(1)
imhist(I1);
title('原始图像直方图')
% 增加对比度：线性变换
figure(2)
subplot(2,2,1);
imshow(I1)
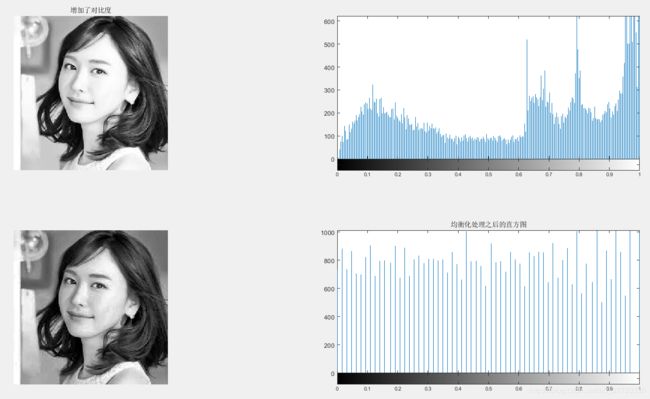
title('增加了对比度')
subplot(2,2,2);
imhist(I1); % 查看增加了对比度的直方图
subplot(2,2,3);
imshow(histeq(I1)); % 均衡化
subplot(2,2,4);
imhist(histeq(I1));
title('均衡化处理之后的直方图')
3.7、直方图规定化
直方图的均衡化算法可以实现自动对灰度均衡化处理，但是我们有时候希望可以控制直方图的形状，按照我们想要的产生。这样就可以有选择地增强某个灰度范围内的对比度或使图像灰度值满足某种特定的分布。这种叫做直方图规定化或者称为直方图匹配。
感觉这样做还不如做分段线性变换来的简单？？？？？
当然不是，直方图规定化还交直方图匹配呢！！！！
理论：直方图规定化是在运用均衡化的原理上，通过建立原始图像和期望图像之间的关系，以使得原始图像匹配特定的形状，从而弥补直方图均衡不具备的交互作用的特性。步骤如下：
（1）先对原始图像均衡化处理：
（2）对待匹配的直方图的图像也进行均衡化处理：
（3）令均衡化之后的像素相等 s = v
（4）对输入图像按（3）变换
I1 = imread('lena.jpg');
I2 = imread('gakki.jpg');
I3 = imread('beauti.jpg');
% I1 = 0.299.*I(:,:,1)+0.587.*I(:,:,2)+0.114.*I(:,:,3); % 转化成灰度图
I1 = im2double(I1);
I2 = im2double(I2); % 为了对矩阵进行计算，这里需要把数据类型转换为float类型
I3 = im2double(I3);
% 计算直方图
[hgram1,~] = imhist(I2);
[hgram2,x] = imhist(I3);
% 直方图均衡化,将标准图的灰度直方图作为原始图的规定化直方图，最重要的一步
J1 = histeq(I1,hgram1);
J2 = histeq(I1,hgram2);
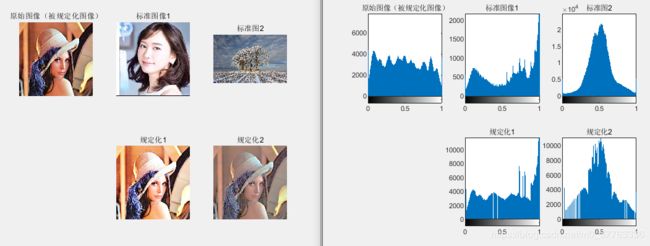
subplot(2,3,1);
imshow(I1);title('原始图像（被规定化图像）');
subplot(2,3,2);
imshow(I2);title('标准图像1');
subplot(2,3,3);
imshow(I3);title('标准图2');
subplot(2,3,5);
imshow(J1);title('规定化1');
subplot(2,3,6);
imshow(J2);title('规定化2');
% 绘制直方图
figure
subplot(2,3,1);
imhist(I1);title('原始图像（被规定化图像）');
subplot(2,3,2);
imhist(I2);title('标准图像1');
subplot(2,3,3);
imhist(I3);title('标准图2');
subplot(2,3,5);
imhist(J1);title('规定化1');
subplot(2,3,6);
imhist(J2);title('规定化2');直方图规定化本质上是一种拟合过程，因此变换得到的直方图与标准目标直方图并不会完全一致，而是近似。而即使是这样，仍然要使规定化的图像在亮度上和对比度上具有类似规定的标准图像特性，这就是直方图规定化的意义。
参考
《精通MATLAB数字图像处理》 张铮