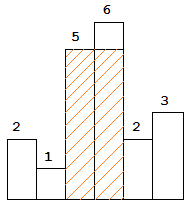
【算法】直方图中最大面积问题
问题描述
给定一个直方图,求这个直方图中最大矩阵对应的面积是多少?
比如有个图如下 (对应的数组为:[2,1,5,6,2,3])
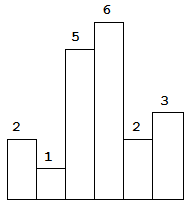
问题分析
这类题是很常见的一道题,也是面试当中很容易考到的一题。解决方法倒是挺多。常见的比如Divide-and-conqure等方法,复杂度也都是O(n log n)。
现在有没有一种更快的方法呢?复杂度可以达到 O(n)
问题求解
解法1:分治法(divide-and-conqure)
分治法,正如其名,需要对该问题分而治之。比如还是上面给定的例子:
- 分:
[2,1,5,6,2,3]分为[2,1,5]和[6,2,3]分别去求解 - 合:最终的最大矩形,不是在左半直方图中,要么是在右半直方图中,或是直接跨越左右直方图。上面子问题直接对应了左半直方图中的最大矩形和右半直方图中的最大矩形。唯一剩下的就是求解第三种情况:跨越左右的直方图
针对上面跨越左右直方图的最大矩形,那么该矩形一定是跨过 [5,6]了。那么可能的情况是 [5,6], [5,6,2,3], [2,1,5,6,2,3],对应的最小高度分别为5,2,1. 因此就需要:从[5,6]出发,不断地根据最小高度扩展这个数组,并在扩展中,获得最大矩形面积即可。
代码就省略了,这个比较简单。复杂度 T(n) = 2 T(n/2) + O(n),因此 T(n) = O(n log n).
解法2:运用STL
解决2比较巧妙,思想如下:
- 1,将数组进行排序,并能获得对应的原始的下标(index)
- 2,不断地插入这些原始下标,并更新最大面积
排序后的原始下标为 [1,0,4,5,2,3],(分别对应原始的 [1,2,2,3,5,6])。
有一个辅助结构(set)用于存储不断加入的下标。先加入2个下标边界(-1和6)
step 0: (-1, 6)
step 1, 插入index 1: (-1, 1, 6), area: (6 - (-1) - 1) * height[1] = 6
step 2, 插入index 0: (-1, 0, 1, 6), area: (1 - (-1) - 1) * height[0] = 2
step 3, 插入index 4: (-1, 0, 1, 4, 6), area: (6 - 1 - 1) * height[4] = 8
…
最后算到的最大的area 为10,end。复杂度:1)开始的下标排序:O(n log n),2)后面各个step中插入下标index,并取得下标的上界和下界,这个用STL的lower_bound就可以实现,总的复杂度也是 O(n log n)。因此总的时间复杂度为 O(n log n)。
给出一份代码:
int largestRectangleArea(vector<int> &height) {
// write your code here
int n = height.size();
vector<long> v(n, 0);
for (int i = 0; i < n; i++) {
long l = height[i];
l = (l << 32) | i;
v[i] = l;
}
sort(v.begin(), v.end());
set<int> st;
st.insert(-1); st.insert(n);
int ans = 0;
for (int i = 0; i < n; i++) {
int idx = 0xffffffff & v[i];
set<int>::iterator iter = lower_bound(st.begin(), st.end(), idx);
int high_idx = *iter;
iter--;
int low_idx = *iter;
//printf("idx:%d, low:%d, high:%d\n", idx, low_idx, high_idx);
ans = max(ans, (high_idx - low_idx - 1) * height[idx]);
st.insert(idx);
}
return ans;
}解法3:用于Stack达到O(n)
第三种方法也是比较巧妙,运用了stack,可以将复杂度降低很多。
思想:
1,有个辅助数组left,left[i]表示以 下标 i 为右边界的矩形,且最小高度为 height[i],所对应的最大area。
2, 有个辅助数组right,跟left类似,只是此时i为左边界。
3,stack中,保存着各个下标,这些下标对应的height,是不断递增的。当要入一个新的元素i时,不断弹出stack中的元素,直到其栈顶的元素对应的height < height[i]。
这样总的过程的复杂度,就是归为:1)从左往右扫描一遍数组,元素放入stack,在某个时机该元素出stack,最后形成left数组;2)从右往左扫描一遍数组,元素放入stack,在某个时机该元素出stack,最后形成right数组. T(n) = O(n)。
附上代码:
int largestRectangleArea(vector<int> &height) {
stack<int> stk;
int n = height.size();
if (n <= 0) return 0;
int ans = 0;
// left[i]: the maximun area ending with index i, with lowest height as height[i];
// right[i]: the maximun area starting with index i, with lowest height as height[i];
vector<int> left(n, 0), right(n, 0);
// scan from left to right
stk.push(0); left[0] = ans;
for (int i = 1; i < n; i++) {
int preIdx = i;
// all the correspoding height in stk should be increasing
while (!stk.empty() && height[stk.top()] >= height[i]) {
stk.pop();
}
// preIdx is the starting (first) index whose height is >= height[i]
preIdx = stk.empty() ? 0 : stk.top() + 1;
left[i] = height[i] * (i - preIdx + 1);
stk.push(i);
}
// scan from right to left
ans = max(ans, height[n-1]);
while (!stk.empty()) stk.pop(); // clear the stk
stk.push(n-1); right[n-1] = height[n-1];
for (int i = n-2; i >= 0; i--) {
int preIdx = i;
while (!stk.empty() && height[stk.top()] >= height[i]) {
stk.pop();
}
preIdx = stk.empty() ? n-1 : stk.top() - 1;
right[i] = height[i] * (preIdx - i + 1);
stk.push(i);
}
for (int i = 0; i < n; i++) ans = max(ans, right[i] + left[i] - height[i]);
return ans;
}