ACM:搜索算法专题(3)——启发式搜索
HihoCoder1312
题目描述:
解答:
·规则:
首先简要说明游戏规则。
游戏的棋局如下:
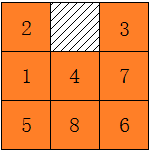
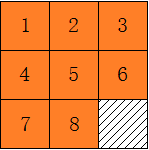
九宫格中放置8个标有不同数字的棋子,其中一个位置为空,通过移动棋子,使得数字有序排列,则游戏完成,如下:
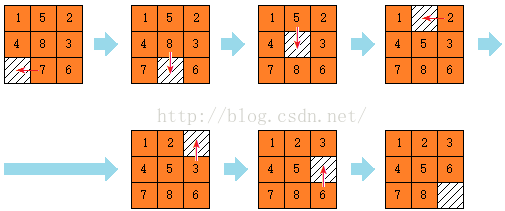
在移动的过程中,只有和空白位置相邻的棋子才可以移动,并仅可以移动到空白位置。下面的例子中可以通过6次移动完成游戏:
以上为游戏规则。
·编码:
本题的思路还是比较简单的。通过dijkstra算法,计算每个棋盘状态到最终状态的最短路径即可。这里的“最短路径”定义为最少的移动的次数。那么首先的问题就是以某种方式记录棋局的状态。方法如下:
假设空白位置记为数字9,那么不同的棋局的数目为:9!= 362880种。如果以字典序将所有的排列方式排序的话,那么每个排列结果就会有唯一的一个编号。因此,编号为1的排列为:123456789,编号为362880的排列为:987654321。所以,目前的问题是给出一个排列,找出它在字典序中的编号。这个问题可以采用一种叫做“康托展开”的方法来求解,方法如下:
对于某一个排列:s[1,2,...9], 定义序列a[1,2,...,9],其中a[i]表示序列s[i+1, i+2, ... 9]中比a[i]小的数值的个数, 例如,排列 9 1 2 3 6 4 7 8 5 对应的a[i] 序列为:8 0 0 2 0 1 0 0。
在给出a[i]序列后,排列s对应的序号为:
X = a[1] * (9 - 1)! + a[2] * (9 - 2)! + ... + a[9] * (9 - 9)!
游戏的目标结果为:1 2 3 4 5 6 7 8 9,对应的序号为1。
·解码:
在知道编码方法后,我们还需要知道如何在给定编号X的情况下,找到对应的排列结果。这个过程是康托展开的逆过程,可以称为“逆康托展开”。方法如下:
① 用X除以(9-1)!得到商q和余数r。
② 从1,2,...9中的尚未使用过的数字中选择第q+1小的数字,该数字就是s[1]。
③ 令: X=r。
④ 反复执行步骤①-③,在每次迭代中依次令X除以(9-2)!, (9-3)!, ..., (9-9)!,就可以依次得到s[2], s[3]...s[9],进而得到对应的排列结果。
下面给出一个例子,求解1-9的排列中,排在第5000的排列结果:
① 令:X=5000, X ÷ (9-1)! = 0...........5000, q=0 r=5000, 当前未使用的数字有{1,2,3, 4,5,6,7,8,9},选择第1小的数字,即1, 因此s[1] = 1。
② 令:X=5000, X ÷ (9-2)! = 0...........5000, q=8 r=5000, 当前未使用的数字有{2,3,4,5,6,7,8,9},选择第1小的数字,即2, 因此s[2] = 2。
③ 令:X=5000, X ÷ (9-3)! = 6...........680, q=6 r=680, 当前未使用的数字有{3,4,5,6,7,8,9},选择第7小的数字,即9, 因此s[3] = 9。
④ 令:X=680, X ÷ (9-4)! = 5...........80, q=5 r=80, 当前未使用的数字有{3,4,5,6,7,8},选择第6小的数字,即8, 因此s[4] = 8。
⑤ 令:X=80, X ÷ (9-5)! = 3...........8, q=3 r=8, 当前未使用的数字有{3,4,5,6,7},选择第4小的数字,即6, 因此s[5] = 6。
⑥ 令:X=8, X ÷ (9-6)! = 1...........2, q=1 r=2, 当前未使用的数字有{3,4,5,7},选择第2小的数字,即4, 因此s[6] = 4。
⑦ 令:X=2, X ÷ (9-7)! = 1...........0, q=1 r=0, 当前未使用的数字有{3,5,7},选择第2小的数字,即5, 因此s[7] = 5。
⑧ 令:X=0, X ÷ (9-8)! = 0...........0, q=0 r=0, 当前未使用的数字有{3,7},选择第1小的数字,即3, 因此s[8] = 3。
⑨ 令:X=0, X ÷ (9-9)! = 0...........0, q=0 r=0, 当前未使用的数字有{7},选择第1小的数字,即7, 因此s[9] = 7。
因此,排在第5000位的排列结果为:1 2 9 8 6 4 5 3 7。
·搜索:
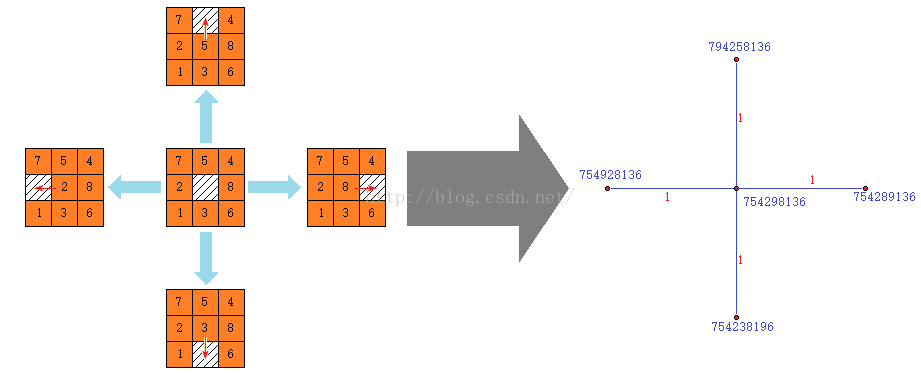
在知道如何将棋局的状态表示为数字后,就可以进行搜索了。我们可以将整个游戏抽象为一个有向图,图中的点为各个不同的棋局状态。而如果两个状态可以通过移动棋子一次达到互相转换,那么,两个点之间就包含一条长度为1的无向边:
构建无向图的工作完成后,可以采用两种方式进行搜索:
方法一:从终点到起点
以最终局面——状态1为起点,运用dijkstra算法进行搜索,就可以知道每一个状态到最终状态的最短距离,然后在接下来给定初始状态后,就可以直接找到对应的最少移动次数。此方法只要搜索一次,就可以对所有的输入的初始状态直接给出答案。
方法二:从起点到终点
也可以在给定起始状态的情况下,进行搜索到达终点的最短距离。此时,对于每一组给出的起始位置,都需要进行一次搜索。为了提高效率,可以采用一种“启发式”的搜索方式对于dijkstra算法进行改进。方法如下:
启发式搜索的思想是:设计一个评估函数F,使用评估函数对于每一个点评估,然后在搜索的过程中优先考虑评估结果较好的点。这样就可以有更高的概率优先找到通向终点的最短路径。
评估函数F由两部分组成:F = G + H,其中G表示从起点到当前点的最短路径长度,初始状态为0,在搜索过程中逐步对G进行赋值;H则表示从当前点到终点的最短距离路径,函数H需要在搜索前进行预估。
搜索过程中维护两个集合:openSet和closeSet,初始状态时,两个集合均为空。搜索步骤如下:
① 将起点的G值设置为0,并设置为当前点。
② 将当前点键入到closeSet中。
③ 搜索所有和当前点邻接的点,如果该点已经在closeSet中,则不做操作,如果该点在openSet中,则更新其G值,比较当前点的G值加1和该临界点已有的G值,取较小者;如果该临界点不在openSet中,则设置该点的G值为当前点G值加1,然后将其加入到openSet中。
④ 选择openSet中F值最小的点作为当前点。
⑤ 反复执行步骤②-④,直到openSet为空或重点已经加入到了closeSet,此时就找到了起点到终点的最短路径。
注意为了保证算法的正确性,评估函数H对于每一个点的函数值一定不能大于其到终点的实际距离。否则在从openSet选择当前搜索点时,就可能会出错,导致无法得到最优解。对于本题,我们则可以定义函数H为:当前状态中的1-8的8个数字的当前位置到目标状态中的8个对应位置的曼哈顿距离之和。由于每次移动会改变一个棋子的位置,导致该棋子的位置到目标位置的曼哈顿距离增大或者减小,如果每次移动都是减小移动棋子到目标位置的曼哈顿距离,那么总的移动次数就是8个棋子到目标位置的曼哈顿距离之和。如果在移动的过程中有些操作会使得移动的棋子的曼哈顿距离变大,那么总的移动次数还要更多。因此这样定义函数H是正确的。
下面的代码采用的是方法一。
输入输出格式:
输入:第1行:1个正整数t,表示数据组数;接下来有t组数据,每组数据有3行,每行3个整数,包含0-8,每个数字只出现一次,其中0表示空位。
输出:第1..t行:每行1个整数,表示该组数据解的步数。若无解输出"No Solution!"
数据范围:
1≤t≤8
程序代码:
/****************************************************/
/* File : Hiho_Week_100 */
/* Author : Zhang Yufei */
/* Date : 2016-05-30 */
/* Description : HihoCoder ACM program. (submit:g++)*/
/****************************************************/
#include
#include
#define NUM 362880
typedef struct node1 vertex;
typedef struct node2 edge;
/*
* Define structure to store the node of graph.
* Parameters:
* @distance: The distance between the current node and the start node.
* @edges: The link list of all the nodes which are adjacent with this node.
* @tag: Mark if the node has been visited.
*/
typedef struct node1 {
int status;
int index;
int distance;
edge *edges;
int tag;
} vertex;
/*
* Define structure to store the edges of the graph.
* Parameters:
* @index: The end point of this edge.
* @next: The next pointer.
*/
typedef struct node2 {
vertex* v;
struct node2 *next;
} edge;
// Record the graph.
vertex graph[NUM];
// Record the multiply value.
int multiply[9] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320};
// Record map.
int map[9];
// Record the Set.
vertex *heap[NUM + 1];
// The size of heap.
int heap_cnt;
/*
* This function compare the distance of the 2 elements in heap.
* Parameters:
* @a & @b: The 2 elements to compare.
* Returns:
* If @a is greater than @b, returns 1; or if @a is equal to @b, returns 0;
* or returns -1;
*/
int cmp(int a, int b) {
if(heap[b]->distance == -1) {
return -1;
} else if(heap[a]->distance == -1) {
return 1;
}else if(heap[a]->distance > heap[b]->distance) {
return 1;
}else if(heap[a]->distance == heap[b]->distance) {
return 0;
} else {
return -1;
}
}
/*
* This function adjusts the array into a heap.
* Parameters:
* @root: The root node of heap.
* Returns:
* None.
*/
void min_heapify(int root) {
int min_index = root;
if(root * 2 <= heap_cnt) {
if(cmp(min_index, 2 * root) > 0) {
min_index = 2 * root;
}
}
if(root * 2 + 1 <= heap_cnt) {
if(cmp(min_index, 2 * root + 1) > 0) {
min_index = 2 * root + 1;
}
}
if(min_index != root) {
vertex *swap = heap[root];
heap[root] = heap[min_index];
heap[min_index] = swap;
heap[root]->index = root;
heap[min_index]->index = min_index;
min_heapify(min_index);
}
}
/*
* This node adjust the heap after update the distance of node.
* Parameters:
* @index: The element to update.
* Returns:
* None.
*/
void update(int index) {
while(index > 1) {
if(cmp(index, index / 2) < 0) {
vertex *swap = heap[index];
heap[index] = heap[index / 2];
heap[index / 2] = swap;
heap[index]->index = index;
heap[index / 2]->index = index / 2;
index /= 2;
} else {
break;
}
}
}
/*
* This function removes the top element from heap.
* Parameters:
* None.
* Returns:
* The element removed.
*/
vertex* remove(void) {
vertex *r = heap[1];
heap[1] = heap[heap_cnt];
heap[1]->index = 1;
heap_cnt--;
min_heapify(1);
return r;
}
/*
* This function transports the map into status number.
* Parameters£º
* None.
* Returns:
* The status number.
*/
int get_status_from_map(void) {
int status = 0;
int tag[10] = {0};
for(int i = 0; i < 9; i++) {
int cnt = 0;
for(int j = 1; j < map[i]; j++) {
if(tag[j] == 0) {
cnt++;
}
}
status += cnt * multiply[8 - i];
tag[map[i]] = 1;
}
return status;
}
/*
* This function transports the status into map.
* Parameters:
* @status: The current status.
* Returns:
* None.
*/
void get_map_from_status(int status) {
int tag[10] = {0};
for(int i = 0; i < 9; i++) {
int s = status / multiply[8 - i];
int cnt = 0;
for(int j = 1; j < 10; j++) {
if(tag[j] == 0) {
cnt++;
if(cnt > s) {
tag[j] = 1;
map[i] = j;
break;
}
}
}
status %= multiply[8 - i];
}
}
/*
* This function computes the edges of each node in graph.
* Parameters:
* @current: The current node.
* Returns:
* None.
*/
void add_edge(int current) {
get_map_from_status(current);
/*if(current == 15331) {
for(int i = 0; i < 9; i++) {
printf("%d ", map[i]);
}
printf("\n");
}*/
for(int j = 0; j < 9; j++) {
if(map[j] == 9) {
if(j + 3 < 9) {
int swap = map[j];
map[j] = map[j + 3];
map[j + 3] = swap;
int status = get_status_from_map();
edge *e = (edge*) malloc(sizeof(edge));
e->v = &graph[status];
e->next = graph[current].edges;
graph[current].edges = e;
swap = map[j];
map[j] = map[j + 3];
map[j + 3] = swap;
}
if(j - 3 >= 0) {
int swap = map[j];
map[j] = map[j - 3];
map[j - 3] = swap;
int status = get_status_from_map();
edge *e = (edge*) malloc(sizeof(edge));
e->v = &graph[status];
e->next = graph[current].edges;
graph[current].edges = e;
swap = map[j];
map[j] = map[j - 3];
map[j - 3] = swap;
}
if(j % 3 != 2 && j + 1 < 9) {
int swap = map[j];
map[j] = map[j + 1];
map[j + 1] = swap;
int status = get_status_from_map();
edge *e = (edge*) malloc(sizeof(edge));
e->v = &graph[status];
e->next = graph[current].edges;
graph[current].edges = e;
swap = map[j];
map[j] = map[j + 1];
map[j + 1] = swap;
}
if(j % 3 != 0 && j - 1 >= 0) {
int swap = map[j];
map[j] = map[j - 1];
map[j - 1] = swap;
int status = get_status_from_map();
edge *e = (edge*) malloc(sizeof(edge));
e->v = &graph[status];
e->next = graph[current].edges;
graph[current].edges = e;
swap = map[j];
map[j] = map[j - 1];
map[j - 1] = swap;
}
break;
}
}
}
/*
* This function computes the shortest distance from the start to every node
* using dijkstra algorithm.
* Parameters:
* @start: The start node.
* Returns:
* None.
*/
void dijkstra(int start) {
for(int i = 0; i < NUM; i++) {
heap[i + 1] = &graph[i];
graph[i].distance = -1;
graph[i].tag = 0;
graph[i].index = i + 1;
}
heap_cnt = NUM;
graph[start].distance = 0;
update(graph[start].index);
while(heap_cnt > 0 && heap[1]->distance != -1) {
vertex *v = remove();
edge *e = v->edges;
while(e != NULL) {
if(e->v->distance == -1 ||
e->v->distance > v->distance + 1) {
e->v->distance = v->distance + 1;
update(e->v->index);
}
e = e->next;
}
}
}
/*
* This function initiates the graph.
* Parameters:
* None.
* Returns:
* None.
*/
void init(void) {
for(int i = 0; i < NUM; i++) {
graph[i].distance = -1;
graph[i].edges = NULL;
graph[i].status = i;
add_edge(i);
}
}
/*
* The main program.
*/
int main(void) {
init();
dijkstra(0);
int t;
scanf("%d", &t);
for(int i = 0; i < t; i++) {
for(int j = 0; j < 9; j++) {
scanf("%d", &map[j]);
if(map[j] == 0) {
map[j] = 9;
}
}
int s = get_status_from_map();
if(graph[s].distance == -1) {
printf("No Solution!\n");
} else {
printf("%d\n", graph[s].distance);
}
}
return 0;
}