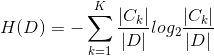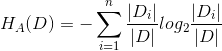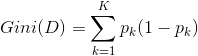《统计学习方法》-李航、《机器学习-西瓜书》-周志华总结+Python代码连载（四）--决策树(Decison-Tree)

一、决策树的概论

决策树是一种基本的分类与回归方法，是表示基于特征对示例进行分类与回归的树形结构。决策树可以转换成一个if-then规则的集合，也可以看作是定义在特征空间划分上的类的条件概率分布。

一般的，一颗决策树包含一个根结点，若干个内部节点和若干个叶结点，每个叶结点对应于决策结果，其他的每个结点则对应于一个属性测试，生成决策树的基本流程遵循‘分而治之’策略。具体算法如下：

---

输入：训练集D={(,),...,(,)};属性集A={,...,}.

过程：

 1.生成节点node;

 2.if D中的样本全属于同一类别C then

 3.   将node标记为C类叶节点；return

 4.end if

 5.if A= or D中样本在A中取值相同 then

 6.   将node标记为叶结点，其类别标记为D中样本数最多的类；return

 7.end if

 8.从A中选择最优划分的属性；

 9.for 的每一个值 do

10.  为node生成一个分支；令表示D中在上取值为的样本子集；

11.   if 为空 then

12.       将分支结点标记为叶结点，其类别标记为D中样本最多的类；return

13.   else

14.        递归该函数；

15.   end if

16.end for

输出：以node为结点的一颗决策树

---

二、决策树中特征选择

2.1 信息增益-应用到ID3算法（选取最大的值）

特征A对训练集D的信息增益g(D,A)，定义训练集D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即：

g(D,A) = H(D)-H(D|A)

其中有:

K-训练集中有K个分类结果，-训练集中分类结果为的统计个数，-训练集中统计样本个数，-特征A将训练集分成n个子集，其中第i个子集的统计个数，-第i个子集中分类为的统计个数。

2.2 信息增益比-应用到C4.5算法（选取最大的值）

特征A对训练集D的信息增益比定义为其信息增益g(D,A)与训练集D关于特征A的值的熵之比，即

其中有：

-为2.1中信息增益

,n是特征A取值的个数。

2.3 基尼指数-应用到CART算法（选取最小的值）

数据集D的纯度可用基尼指数来度量：

,-训练集中分类为的概率

在特征A的条件下，训练集D的基尼指数定义为：，其中有特征A取值{,...,}s个取值，所以上面的基尼指数是为是否A=分成两个子集，一个特征需要计算s个Gini(D,A)的值。

上述三个指标可分别套用到一中的基本决策树的生成算法。

三、决策树的剪枝

决策树采用递归的方法生成的，往往容易过拟合。为了防止过拟合，采用决策树剪枝，主要为前剪枝和后剪枝。

3.1 前剪枝(预剪枝)：在未用选择好的特征，全部认为是其中一类计算出评估指标的值，然后计算使用了该特征后的评估指标的值，有提升使用该特征，否则丢弃不使用。

3.2 后剪枝：在生成好的一颗决策树上进行剪枝，考虑某一个结点，把该结点看成是一个也结点，计算评估指标是否有所提升。

代码实现：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
get_ipython().run_line_magic('matplotlib', 'inline')

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
import math
from math import log
import pprint


def create_data():
    datasets = [['青年', '否', '否', '一般', '否'],
               ['青年', '否', '否', '好', '否'],
               ['青年', '是', '否', '好', '是'],
               ['青年', '是', '是', '一般', '是'],
               ['青年', '否', '否', '一般', '否'],
               ['中年', '否', '否', '一般', '否'],
               ['中年', '否', '否', '好', '否'],
               ['中年', '是', '是', '好', '是'],
               ['中年', '否', '是', '非常好', '是'],
               ['中年', '否', '是', '非常好', '是'],
               ['老年', '否', '是', '非常好', '是'],
               ['老年', '否', '是', '好', '是'],
               ['老年', '是', '否', '好', '是'],
               ['老年', '是', '否', '非常好', '是'],
               ['老年', '否', '否', '一般', '否'],
               ]
    labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
    # 返回数据集和每个维度的名称
    return datasets, labels

datasets, labels = create_data()
train_data = pd.DataFrame(datasets, columns=labels)
train_data

# 熵
def calc_ent(datasets):
    data_length = len(datasets)
    label_count = {}
    for i in range(data_length):
        label = datasets[i][-1]
        if label not in label_count:
            label_count[label] = 0
        label_count[label] += 1
    ent = -sum([(p / data_length) * log(p / data_length, 2)
                for p in label_count.values()])
    return ent


# 经验条件熵
def cond_ent(datasets, axis=0):
    data_length = len(datasets)
    feature_sets = {}
    for i in range(data_length):
        feature = datasets[i][axis]
        if feature not in feature_sets:
            feature_sets[feature] = []
        feature_sets[feature].append(datasets[i])
    cond_ent = sum(
        [(len(p) / data_length) * calc_ent(p) for p in feature_sets.values()])
    return cond_ent


# 信息增益
def info_gain(ent, cond_ent):
    return ent - cond_ent


def info_gain_train(datasets):
    count = len(datasets[0]) - 1
    ent = calc_ent(datasets)
#     ent = entropy(datasets)
    best_feature = []
    for c in range(count):
        c_info_gain = info_gain(ent, cond_ent(datasets, axis=c))
        best_feature.append((c, c_info_gain))
        print('特征({}) - info_gain - {:.3f}'.format(labels[c], c_info_gain))
    # 比较大小
    best_ = max(best_feature, key=lambda x: x[-1])
    return '特征({})的信息增益最大，选择为根节点特征'.format(labels[best_[0]])

info_gain_train(np.array(datasets))

# 定义节点类 二叉树
class Node:
    def __init__(self, root=True, label=None, feature_name=None, feature=None):
        self.root = root
        self.label = label
        self.feature_name = feature_name
        self.feature = feature
        self.tree = {}
        self.result = {
            'label:': self.label,
            'feature': self.feature,
            'tree': self.tree
        }

    def __repr__(self):
        return '{}'.format(self.result)

    def add_node(self, val, node):
        self.tree[val] = node

    def predict(self, features):
        if self.root is True:
            return self.label
        return self.tree[features[self.feature]].predict(features)


class DTree:
    def __init__(self, epsilon=0.1):
        self.epsilon = epsilon
        self._tree = {}

    # 熵
    @staticmethod
    def calc_ent(datasets):
        data_length = len(datasets)
        label_count = {}
        for i in range(data_length):
            label = datasets[i][-1]
            if label not in label_count:
                label_count[label] = 0
            label_count[label] += 1
        ent = -sum([(p / data_length) * log(p / data_length, 2)
                    for p in label_count.values()])
        return ent

    # 经验条件熵
    def cond_ent(self, datasets, axis=0):
        data_length = len(datasets)
        feature_sets = {}
        for i in range(data_length):
            feature = datasets[i][axis]
            if feature not in feature_sets:
                feature_sets[feature] = []
            feature_sets[feature].append(datasets[i])
        cond_ent = sum([(len(p) / data_length) * self.calc_ent(p)
                        for p in feature_sets.values()])
        return cond_ent

    # 信息增益
    @staticmethod
    def info_gain(ent, cond_ent):
        return ent - cond_ent

    def info_gain_train(self, datasets):
        count = len(datasets[0]) - 1
        ent = self.calc_ent(datasets)
        best_feature = []
        for c in range(count):
            c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
            best_feature.append((c, c_info_gain))
        # 比较大小
        best_ = max(best_feature, key=lambda x: x[-1])
        return best_

    def train(self, train_data):
        """
        input:数据集D(DataFrame格式)，特征集A，阈值eta
        output:决策树T
        """
        _, y_train, features = train_data.iloc[:, :
                                               -1], train_data.iloc[:,
                                                                    -1], train_data.columns[:
                                                                                            -1]
        # 1,若D中实例属于同一类Ck，则T为单节点树，并将类Ck作为结点的类标记，返回T
        if len(y_train.value_counts()) == 1:
            return Node(root=True, label=y_train.iloc[0])

        # 2, 若A为空，则T为单节点树，将D中实例树最大的类Ck作为该节点的类标记，返回T
        if len(features) == 0:
            return Node(
                root=True,
                label=y_train.value_counts().sort_values(
                    ascending=False).index[0])

        # 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
        max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
        max_feature_name = features[max_feature]

        # 4,Ag的信息增益小于阈值eta,则置T为单节点树，并将D中是实例数最大的类Ck作为该节点的类标记，返回T
        if max_info_gain < self.epsilon:
            return Node(
                root=True,
                label=y_train.value_counts().sort_values(
                    ascending=False).index[0])

        # 5,构建Ag子集
        node_tree = Node(
            root=False, feature_name=max_feature_name, feature=max_feature)

        feature_list = train_data[max_feature_name].value_counts().index
        for f in feature_list:
            sub_train_df = train_data.loc[train_data[max_feature_name] ==
                                          f].drop([max_feature_name], axis=1)

            # 6, 递归生成树
            sub_tree = self.train(sub_train_df)
            node_tree.add_node(f, sub_tree)

        # pprint.pprint(node_tree.tree)
        return node_tree

    def fit(self, train_data):
        self._tree = self.train(train_data)
        return self._tree

    def predict(self, X_test):
        return self._tree.predict(X_test)

datasets, labels = create_data()
data_df = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(data_df)
tree

# 使用sklearn使用

# data
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = [
        'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
    ]
    data = np.array(df.iloc[:100, [0, 1, -1]])
    # print(data)
    return data[:, :2], data[:, -1]


X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
import graphviz


clf = DecisionTreeClassifier()
clf.fit(X_train, y_train,)

连载GitHub同步更新：https://github.com/wenhan123/ML-Python-