有限序列线性复杂度和k-错线性复杂度的计算 —— 密码与密码工程实践No.2
有限序列线性复杂度和k-误差线性复杂度的计算
在本节中,我们的目标是开发算法,计算有限序列的线性复杂度和k-误差线性复杂度,将其视为周期为2次方的二进制序列的初始段(我们不需要知道是哪一次方)。
注意,任何周期为 2 v {{2}^{v}} 2v的无穷序列 s ∈ T s\in \Tau s∈T,其中 最小, c ( s ) ≤ 2 v c(s)\le {{2}^{v}} c(s)≤2v。因此,如果我们知道s的至少 2 c ( s ) 2c(s) 2c(s)项,我们实际上知道序列的整个周期,即我们知道整个序列。
我们将用 表示周期任意幂为2的二进制序列集, T = ⋃ i = 0 ∞ P 2 i \Tau =\bigcup\nolimits_{i=0}^{\infty }{{{P}_{{{2}^{i}}}}} T=⋃i=0∞P2i。
定理3.1 假设 z = ( z 0 , z 1 , ⋯ , z t − 1 ) ∈ F 2 t z=({{z}_{0}},{{z}_{1}},\cdots ,{{z}_{t-1}})\in F_{2}^{t} z=(z0,z1,⋯,zt−1)∈F2t 是一个长度为 t ≥ 1 t\ge 1 t≥1的有限序列。
定义 u = ⌈ log 2 t ⌉ u=\left\lceil {{\log }_{2}}t \right\rceil u=⌈log2t⌉ ,无限周期为 2 u {{2}^{u}} 2u的序列 s ′ {{s}^{'}} s′如下:
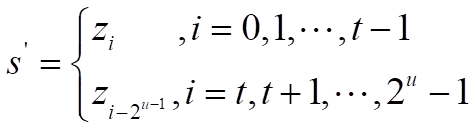
- 如果 c ( z , T ) ≤ t 2 c(z,\Tau )\le \frac{t}{2} c(z,T)≤2t , 则 c ( z , T ) = c ( s ′ ) c(z,\Tau )=c({{s}^{'}}) c(z,T)=c(s′) ;
- 如果 c ( z , T ) > t 2 c(z,\Tau )>\frac{t}{2} c(z,T)>2t , 则 c ( s ′ ) > t 2 c({{s}^{'}})>\frac{t}{2} c(s′)>2t 。
前面的定理可用于计算有限序列的线性复杂度,如下所示。对于长度为t的有限序列z,将其看作一个周期序列的初始段,在定理3.1中建立(线性时间)周期 2 ⌈ log 2 t ⌉ {{2}^{\left\lceil {{\log }_{2}}t \right\rceil }} 2⌈log2t⌉ 2的无穷序列 s ′ {{s}^{'}} s′。然后使用Games-Chan算法计算 c ( s ′ ) c({{s}^{'}}) c(s′)。如果结果最多是 t 2 \frac{t}{2} 2t,我们将其输出为 c ( z , T ) c(z,\Tau ) c(z,T)。否则,我们输出一条消息“z的复杂度大于项数的一半”。当我们真正想计算只知道第一个t项的无限序列s的复杂度时,这种情况可能很有用。
然而,我们可能需要计算 c ( z , T ) c(z,\Tau ) c(z,T)的精确值,即使它比 t 2 \frac{t}{2} 2t高。这一点,以及k-错误复杂度可以使用以下定理计算。其主要思想是,如果我们将有限序列扩展为无限周期代价序列,例如序列中的新项都是具有零代价的,那么对新项的任何更改都不计入k个错误,只计入原始有限序列中的更改。
定理3.2 假设 z = ( z 0 , z 1 , ⋯ , z t − 1 ) ∈ F 2 t z=({{z}_{0}},{{z}_{1}},\cdots ,{{z}_{t-1}})\in F_{2}^{t} z=(z0,z1,⋯,zt−1)∈F2t是一个有限序列,其中 t ≥ 1 t\ge 1 t≥1。定义 u = ⌈ log 2 t ⌉ u=\left\lceil {{\log }_{2}}t \right\rceil u=⌈log2t⌉,定义周期为 2 u 2^u 2u的无限代价序列 s ′ {{s}^{'}} s′ ,如下所示:
s i ′ = z i s_{i}^{'}={{z}_{i}} si′=zi , cos t [ i ] = 1 \cos t[i]=1 cost[i]=1 , i = 0 , 1 , ⋯ , t − 1 i=0,1,\cdots ,t-1 i=0,1,⋯,t−1
∀ s i ′ \forall s_{i}^{'} ∀si′ , cos t [ i ] = 0 \cos t[i]=0 cost[i]=0 , i = t , t + 1 , ⋯ , 2 u − 1 i=t,t+1,\cdots ,{{2}^{u}}-1 i=t,t+1,⋯,2u−1
c k ( z , T ) = c k , 2 u ( s ′ , cos t ) {{c}_{k}}(z,\Tau )={{c}_{k,{{2}^{u}}}}({{s}^{'}},\cos t) ck(z,T)=ck,2u(s′,cost) , k = 0 , 1 , ⋯ , w t ( z ) k=0,1,\cdots ,wt(z) k=0,1,⋯,wt(z)
特别地, c 0 ( z , T ) = c 0 , 2 u ( s ′ , cos t ) {{c}_{0}}(z,\Tau )={{c}_{0,{{2}^{u}}}}({{s}^{'}},\cos t) c0(z,T)=c0,2u(s′,cost)