CenterNet：Objects as Points论文解读以及源码分析

ICCV2019 官方源码

梗概

CenterNet通过预测每个目标的中心点，既而以中心点为基准进行回归宽和高，以及由于下采样带来的点的偏置。将目标检测用关键点检测的思路来做，抛弃了由anchor生成的大量需要被抑制的样本，故而不需要NMS做后处理，而且整个网络只有一个检测Head，不基于FPN为BackBone需要多个检测Head，整体速度就快了很多。

方法

网络的总体结构可以化简为上图所示。其中backbone的结构放在最后讲解，对于一种新的检测思路，重点思路是在如何对label编码，如何对预测结果解码上。实际上论文的顺序也是最后介绍backbone。

检测头

假设我们已经得到了一个从backbone中得到的特征图，其shape为$R^{h,w,D}$, h和w是原图的1/4。这个特征经过检测Head，得到了三样东西

• key point heatmap： shape是 $h\times w\times C$, c是类别数目，就是每个类别都有自己的单通道的heatmap。热图上的峰值对应了图像的一个目标（属于热图对应的类别）。
• Offset： 因为是预测目标中心的位置。如果一个在原图的目标的中心坐标为x，y。那这个目标对应在特征图上的位置就是 x//4, y // 4。 这里用的是整除。 这个数字乘以4得到的数值就不会是原图坐标了。所以从heatmap上取到的峰值位置，未必等于原图上目标的中心点。还需要一个偏置项，描述了heatmap上的取到的峰值位置离原图坐标下最终的目标的一个偏移量。
• Size： shape和offset一致，都是2通道的map。两个通道分别描述目标的height和width。

所以总的输出通道为C+4。相较于Anchor Base的检测网络，需要N* K*(C+4)，是不是小了很多呢。N是检测头的数目，K是anchor的数目

Label的编码

三个分支的意义大家知道了，那三个分支对应的标签应该是啥呢？

• heatmap：既然heatmap是预测目标的中心位置。那么对于一张图像中的一个目标$O^{c,x,y}$在图像上x，y的位置上，且所属类别C。我们就应该在第C个类别对应的heatmap上，在[x//4, y//4]的位置上设置为1。但是仅仅这样是不够的，一个目标的中心点是通过暴力的求平均得到的，网络在训练初期很难理解，为啥离中心点一个像素单元的地方就变成了负样本了。就是说网络比较难get到什么是物体的中心。因为还需要用一个高斯核对每个位置重新赋值一个label，这个label是在0-1之间，相当于起到了一个软标签的效果。离目标中心越远的位置，其label值越接近0。 重叠位置的label赋值选择二者的最大值。（其实也是关键点检测常用的编码label的方法）
• offSet： 如果你理解了offset的用途。那不难理解如何训练Offset。我们希望offset输出的是 原始坐标整除stride和不整除stride 的差值。所以目标$O^{c,x,y}$在offset上对应的label就是 在 [x//4, y//4]上的值为 [x / 4 - x // 4, y / 4 - y // 4]
• Size：基于上面的两个分支，我们已经可以准确获得目标在原图坐标系下的中心点了。接下里，希望Size输出基于峰值位置上目标框的高和宽。假设这个目标的GT框是（x1，y1; x2, y2)， 则这个位置的label是 （x2 - x1; y2 - y1)。 注意是在原图坐标下计算的，没有除以stride。同时尺度过大，作者在size分支的loss上乘上了0.1这个系数。loss放在后面说。

label的解码

在inference的过程中，得到三个分支的特征图之后，如何解码呢？

1. 首先得到峰值位置（x,y），据作者说，用3x3的最大池化就能找到。转到源码分析部分。
2. 加上（x,y）位置上的offset结果。 然后乘以4，映射到原图坐标下。
3. 得到（x,y）位置上Size结果。 然后加加减减就能得到框的左上角坐标和右下角坐标了

训练

在介绍了三个分支的label编码之后，自然来谈谈loss。

• heatmap分支：用focal loss做二分类。对每一个通道（每个类别）都做。也是FCOS，RetainNet中常用的class分支的训练方式。除以正样本数目N。
• 剩下两个分支都是L1 loss。除以正样本数目N。（仅仅是目标中心的位置参与loss，哪怕靠近中心的位置都不参与loss的计算，也就是被ignore了，并不是被判负）

总的loss是
$$loss=L_{heatmap}+L_{offset}+0.1\ast L_{size}$$

作者也提到，中心点附近的其他位置并不是直接判负。而是用的reduced negative loss。就是说附近的点是负样本，但他们的label不是0.而是0-1的值。越接近0代表这个位置越可能是非目标的中心。

backbone

作者在论文中使用了三种backbone。分别是：

• Hourglass：这个网络最开始被提出就是用来做关键点检测的。作者改为stacked的方式，就类似渐进式或者干脆说级联。就是一个encoder-decoder之后还接一个encoder-decoder。程明明组下的BASNet，做显著性检测的论文也是用的这种backbone。
• ResNet： 作者魔改了一下，在每个上采样之前添加一个DCN（变形卷积）
• DLA： 一个做分类的网络。

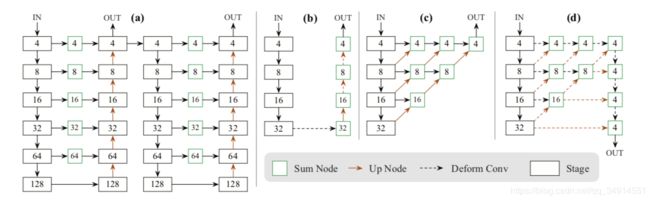
（a）：hourglass ； （b）：魔改的resNet； （d）作者魔改的DLA

源码分析

按照惯例，还是来看看源码。对照论文验证一下。

1. 首先看看解码的地方。在 process中，获得模型的三个分支的预测结果

hm = output['hm'].sigmoid_() # heatmap
wh = output['wh']  # size
reg = output['reg'] if self.opt.reg_offset else None  # offset

然后进入ctdet_decode 这个函数按功能可以分三部分

nms: 获得heatmap上的极值位置
topk ： 这些极值位置上的前k个概率大的位置
得到目标框

NMS的部分很简单，用map pool获得3*3的格子中最大的值，然后和之前的输入对比一下就可以得到极值位置

 hmax = nn.functional.max_pool2d(
        heat, (kernel, kernel), stride=1, padding=pad)
keep = (hmax == heat).float()

topk省略不介绍。
xs是中心位置， reg是offset。他们相加，就是准确的目标中心位置

 xs = xs.view(batch, K, 1) + reg[:, :, 0:1]
 ys = ys.view(batch, K, 1) + reg[:, :, 1:2]

然后加加减减就得到框的位置了。

 bboxes = torch.cat([xs - wh[..., 0:1] / 2, 
                        ys - wh[..., 1:2] / 2,
                        xs + wh[..., 0:1] / 2, 
                        ys + wh[..., 1:2] / 2], dim=2)

唯独和论文有出入的地方，是没有乘上4（stride）。我找了很久也没找到这个stride。我怀疑作者在训练时候，size的label就是除以4的了。
这个时候，我们得到的是原图小4倍的坐标。然后在根据具体图像大小还原回去就行了。

然后看看dataset里面的一些细节：

• 高斯核的方差，是根据目标框的大小自动改变的。

radius = gaussian_radius((math.ceil(h), math.ceil(w)))

• heatmap的label制作过程：

def draw_umich_gaussian(heatmap, center, radius, k=1):
  diameter = 2 * radius + 1
  gaussian = gaussian2D((diameter, diameter), sigma=diameter / 6)  # 先得到一个大小的高斯核
  
  x, y = int(center[0]), int(center[1]) # 目标中心

  height, width = heatmap.shape[0:2]
    
  left, right = min(x, radius), min(width - x, radius + 1)
  top, bottom = min(y, radius), min(height - y, radius + 1)
  # 然后把高斯核的某部分贴到以目标中心为中心的一片相同大小的区域上；如果重叠，取较大值。
  masked_heatmap  = heatmap[y - top:y + bottom, x - left:x + right]
  masked_gaussian = gaussian[radius - top:radius + bottom, radius - left:radius + right]
  if min(masked_gaussian.shape) > 0 and min(masked_heatmap.shape) > 0: # TODO debug
    np.maximum(masked_heatmap, masked_gaussian * k, out=masked_heatmap)
  return heatmap