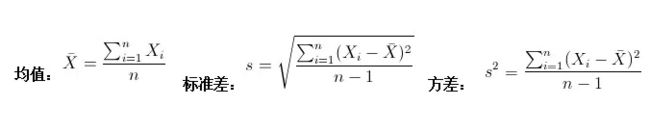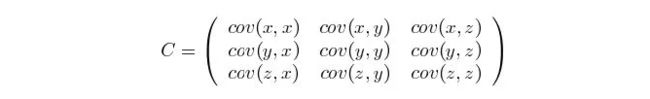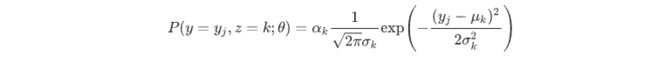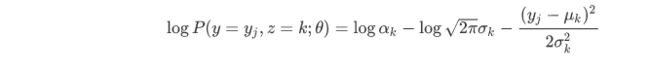李航《统计学习方法》学习笔记之——第九章：EM算法及其推广（高斯混合模型）

“李航《统计学习方法》学习笔记” 系列教程以李航老师《统计学习方法》为基础，系列笔记内容主要包括我学习过程中对于书中算法原理的理解和重点知识的汇总。

由于能力有限，不足支持请大家多多指正，大家有什么想法也非常欢迎留言评论！

关于我的更多系列学习笔记，欢迎您关注“武汉AI算法研习”公众号！

本文分三个部分“【针对朴素贝叶斯法的理解】”、“【朴素贝叶斯算法原理】”、“【文本分类上应用】”来进行展开，总共阅读时间大约10分钟。

【针对高斯混合模型的理解】

1、仍然是一个概率模型，高斯混合模型是对高斯模型进行简单的扩展，GMM使用多个高斯分布的组合来刻画数据分布，每个高斯分模型就代表了一个类（一个Cluster），对样本中的数据分别在几个高斯模型上投影，就会分别得到在各个类上的概率；

2、所有高斯分量的权重系数大于零，且和为1；

3、混合高斯模型中待求的参数θ包括每个分量的高斯分布均值和方差，各个分量权重；

4、初始化GMM时，一般传入“混合高斯分布分量数”、“约定协方差矩阵属性（高斯分布的形状）”、“EM迭代运行次数”；

5、GMM里，BIC(Bayesian Information Criteria)准则是一种有效的成分数确定方法；

6、GMM和K-means很像，只是GMM是学习出一些概率密度函数，给出每个点到每个类的概率，所以GMM除了可以用作聚类，也可以用作密度估计；

7、GMM得出的所属类别概率值，在很多场合适用性更强（概率值连续性），比单纯的得出分类结果更具有可解释性；

8、EM 算法具备收敛性，但并不保证找到全局最大值，有可能找到局部最大值。解决方法是初始化几次不同的参数进行迭代，取结果最好的那次。

 

【GMM的数学原理】

此处部分参考李航《统计学习方法》，本书pdf详情，公众号可回复“统计学习方法”获取。

1、数学基本含义

样本均值和方差：一维样本数据特征中，样本均值和标准差计算简单，样本均值反应了样本集合的中间点，标准差和方差则描述了样本点的离散程度。

协方差和协方差矩阵：协方差可以描述可以描述两个统计量之间的相关性，当协方差大于0，则说明两个变量呈现正相关；同时在二维变量中可以简单依据定义得到协方差，但是如果是多维情况下，这就需要协方差矩阵来表示各个变量之间的相互关系了，协方差矩阵上对角线就是各个变量的方差。

协方差矩阵还可以这样计算，先让样本矩阵中心化，即每一维度减去该维度的均值，使每一维度上的均值为0，然后直接用新的到的样本矩阵乘上它的转置，然后除以(N-1)即可。

% Matlab源码：中心化样本矩阵，使各维度均值为0
X = MySample - repmat(mean(MySample),10,1);
C = (X'*X)./(size(X,1)-1);

2、GMM运用EM算法步骤

通过 EM 迭代更新高斯混合模型参数的方法,假设我们有样本数据  和一个有  个子模型的高斯混合模型，想要推算出这个高斯混合模型的最佳参数。

2.1 首先初始化参数

方案1：协方差矩阵设为单位矩阵，每个模型比例的先验概率；均值设为随机数。

方案 2：由k均值（k-means）聚类算法对样本进行聚类，利用各类的均值作为，并计算，取各类样本占样本总数的比例。

2.2 E步：依据当前参数，计算每个数据  来自子模型  的可能性

2.3 M步：计算新一轮迭代的模型参数

2.4 重复计算E步和M步，直到收敛（  ,  是一个很小的正数，表示经过一次迭代之后参数变化非常小）

 

3、GMM的纯数学推导（相比《统计学学习方法》更加明晰）

3.1 E步，确定Q函数

定义观察变量y，定义隐变量为z，则完全数据的对数似然函数为：

为了计算方便，其对数式为：

则有Q函数为：

以上Q函数中的，后验概率为：

3.2 M步

M步计算可参考《统计学习方法》，为了求参数需要求取偏导数并令其为0。

 

 

【参考文献】

[1] 高斯混合模型（理论+opencv实现）

[2] 浅谈协方差矩阵

[3] 从最大似然函数 到 EM算法详解