词法分析——NFA 转换成 DFA： 子集构造算法

因为 NFA 的状态转移不确定，不适合直接做词法分析器的识别，在写算法时往往需要使用回溯。所以我们一般使用子集构造算法，将 NFA 转换成 DFA，得到确定的状态转移，再转化成一个词法分析器的代码。

下面给出一个关于 NFA 到 DFA 转化的例子，我们使用 a(b|c)* 做例：

对于$ϵ$的边表示一种零代价的转换，$n_1$可以在没有任何输入操作的情况下直接滑动到$n_2$

所以$n_0$通过 a 可以走到 $n_1,n_2,n_3,n_4,n_6,n_9$。我们可以将这样的 6 个元素记为一个集合 $q_1$。 $q_1=\{n_1,n_2,n_3,n_4,n_6,n_9\}$。

$q_1$ 通过 b 可以得到：$n_5,n_8,n_9,n_3,n_4,n_6$ ，记为$q_2$。

$q_2$继续通过某一节点得到$q_3$

继续重复该步骤，得到所有的子集。

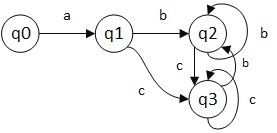
所以$q_0$通过 a 得到$q_1,q_1$通过 b 得到$q_2$…，最终可以将 NFA 转化为一个 DFA。

新的DFA中的状态只要包含原NFA中任意一终结状态，其就是终结状态，例如原NFA中终结状态有$n_9$，则$q_1,q_2$在DFA中都是终结状态

对于子集的求解，首先我们先看出在 NFA 中的下一状态，如$q_1$的下一状态记为 $\delta (q_1)$， 在这里是 {$n_5$} 。之后求它的边界， 即每一个元素都通过$ϵ$能走到的所有状态，记为$\delta (q_1)$的$ϵ$闭包。

对算法的讨论

• 不动点算法
  • 算法可以提前运行终止，因为状态数是有限的
• 时间复杂度
  • 最坏的情况$O(2^N)$
  • 但是实际中不常发生，因为并不是每个子集都会出现的，
  • 像上面的例子中，有$n_0$到$n_9$十个元素，本来应该最多发生$2^{10}$次，实际上只发生了3次，$q_1,q_2$和$q_3$。

ε-闭包的计算：深度优先

/* ε-closure： 基于深度优先遍历的算法 */
set closure = {};
void eps_closure(x){
    closure += {x};  // 集合的加法， 并
    foreach(y: x --ε--> y){  // y 是 x 通过 ε 转换到的 y。
        if(!visited(y)){     // 如果 y 还没有访问过，就访问 y
            eps_closure(y); 
        }
    }
}

算法的时间复杂度是O(N)

ε-闭包的计算：宽度优先

/* ε-closure： 基于宽度优先遍历的算法 */
set closure = {};
Q = [];    // quenu 基于队列的概念，
void eps_closure(x) = 
    Q = [x];
    while(Q not empty)
    q <- deQueue(Q)
    closure += q
    foreach(y: q --ε--> y)  // 将所有的从 Q 开始可以走到的 y 都加到 Q 里
        if(!visited(y))
            enQueue(Q,y)

对于第一个例子，算法执行过程如下：

q0 <- eps_closure(n0)   // q0 = {n0}
Q <- {q0}       // Q = {q0}
workList <- q0     // workList = [q0, ...]
while(workList != [])   
    remove q from workList   // workList = [...]
    foreach(character c)     // c = a
        t <- e-closure(delta(q,c))   // delta(q0, a) = {n1}, t = {n1, n2, n3, n4, n6, n9}
        D[q,c] <- t    //   q1 = t
        if(t not in Q)    // Q = {q0, q1} , workList = [q1]
            add t to Q and workList

重复运行上式代码，运行内层循环可以得到

$q_1=\{n_1,n_2,n_3,n_4,n_6,n_9\}$
$q_2=\{n_5,n_8,n_9,n_3,n_4,n_6\}$
$q_3=\{n_7,n_8,n_9,n_3,n_4,n_6\}$

回到外层循环后，再次运行， 不能得到新的子集。

所以使用图像表示，结果如下：