MATLAB实验(四)—— 数字滤波器设计
文章目录
- 一、实验目的:
- 二、实验内容及要求:
- 1. 双线性变换法设计IIR数字滤波器:
- 2. 窗函数法设计FIR数字滤波器:
- 三、实验结果及问题回答:
一、实验目的:
设计传输函数,使其频率响应逼近给定的频率响应指标。本实验掌握双线性变换法设计IIR数字滤波器的原理及具体设计方法;掌握窗函数法设计FIR数字滤波器的原理及具体设计方法。
二、实验内容及要求:
1. 双线性变换法设计IIR数字滤波器:
用双线性变换法及Mat lab编程设计一个IIR数字带通滤波器,其中通带波纹为1dB,阻带最小衰减为40dB,通带截止频率分别为500Hz和700Hz,阻带截止频率分别为400Hz和800Hz,抽样频率为2000Hz。画出该滤波器的幅频特性图。
2. 窗函数法设计FIR数字滤波器:
用窗函数法(汉明窗)及Mat lab编程设计一个FIR数字带通滤波器,其中通带波纹为1dB,阻带最小衰减为40dB,通带截止频率分别为500Hz和700Hz,阻带截止频率分别为400Hz和800Hz,抽样频率为2000Hz。画出该滤波器的幅频特性图。
三、实验结果及问题回答:
- 双线性变换法设计IIR数字滤波器:
(1)程序:
clc;clear all;
Rp = 1; % bandpass attenuation in dB
Rs = 40; % bandstop attenuation in dB
OmegaP1_1=500; % bandpass edge frequency
OmegaP1_2=700; % bandpass edge frequency
OmegaS1_1=400; % bandstop edge frequency
OmegaS1_2=800; % bandstop edge frequency
Fp=2000; % samling frequency
Wp1=2*pi*OmegaP1_1/Fp; % change analogy frequency to digital angular frequency
Wp2=2*pi*OmegaP1_2/Fp; % change analogy frequency to digital angular frequency
Ws1=2*pi*OmegaS1_1/Fp; % change analogy frequency to digital angular frequency
Ws2=2*pi*OmegaS1_2/Fp; % change analogy frequency to digital angular frequency
OmegaP1=tan(Wp1/2); % nonlinearlization
OmegaP2=tan(Wp2/2); % nonlinearlization
OmegaS1=tan(Ws1/2); % nonlinearlization
OmegaS2=tan(Ws2/2); % nonlinearlization
OmegaP0=sqrt(OmegaP1*OmegaP2);% equivalent mid frequency
Bw=OmegaP2-OmegaP1; % bandwith
Eta_P0=OmegaP0/Bw; % Normalization
Eta_P1=OmegaP1/Bw; % Normalization
Eta_P2=OmegaP2/Bw; % Normalization
Eta_S1=OmegaS1/Bw; % Normalization
Eta_S2=OmegaS2/Bw; % Normalization
Lemta_P_EquivalentLowPass=(Eta_P2^2-Eta_P0^2)/Eta_P2; % change to the equivalent Lowpass patameter
Lemta_S1_EquivalentLowPass=-(Eta_S1^2-Eta_P0^2)/Eta_S1; % change to the equivalent Lowpass patameter
Lemta_S2_EquivalentLowPass=(Eta_S2^2-Eta_P0^2)/Eta_S2; % change to the equivalent Lowpass patameter
Lemta_S_EquivalentLowPass=min(Lemta_S1_EquivalentLowPass,Lemta_S2_EquivalentLowPass); % get the smallest
% Estimate the Filter Order
[N, Wn] = buttord(Lemta_P_EquivalentLowPass, Lemta_S_EquivalentLowPass, Rp, Rs,'s');
% Design the Filter
[num1,den1] = butter(N,Wn,'s');
[num2,den2]=lp2bp(num1,den1,OmegaP0,Bw);
[num,den]=bilinear(num2,den2,0.5);
% Compute the gain response
w = 0:pi/255:pi;
h = freqz(num,den,w);
g = 20*log10(abs(h));
% Plot the gain response
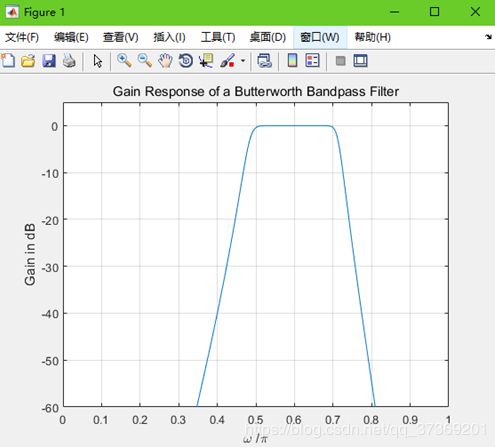
figure;
plot(w/pi,g);grid
axis([0 1 -60 5]);
xlabel('\omega /\pi'); ylabel('Gain in dB');
title('Gain Response of a Butterworth Bandpass Filter');
(2)幅频特性:
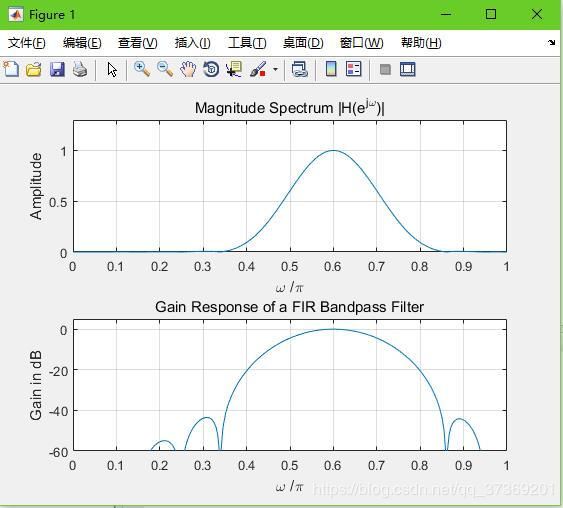
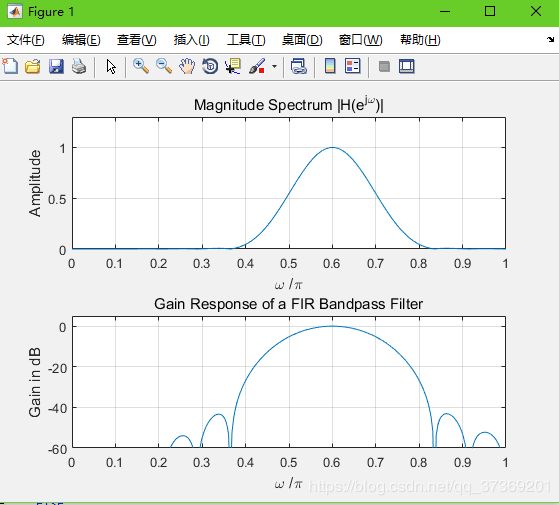
2. 窗函数法设计FIR数字滤波器:
(1)程序:
汉宁:
clc;
clear;
Rs = 40; % bandstop attenuation in dB
OmegaP1_1=500; % bandpass edge frequency
OmegaP1_2=700;% bandpass edge frequency
OmegaS1_1=400; %bandstop edge frequency
OmegaS1_2=800; %bandstop edge frequency
Ft=2000; % samling frequency
Wn=2/Ft*[OmegaP1_1 OmegaP1_2];% change analogy frequency to digital angular frequency
N = 21;num=fir1(N,Wn,hann(N+1));%汉宁
w = 0:pi/255:pi;
h = freqz(num,1,w);
g = 20*log10(abs(h));
% 幅频绘制
subplot(2,1,1);
plot(w/pi,abs(h));grid
axis([0 1 0 1.3]);
title('Magnitude Spectrum |H(e^{j\omega})|');
xlabel('\omega /\pi');
ylabel('Amplitude');
% 增益绘制
subplot(2,1,2);
plot(w/pi,g);grid
axis([0 1 -60 5]);
xlabel('\omega /\pi'); ylabel('Gain in dB');
title('Gain Response of a FIR Bandpass Filter');
海明:
clc;
clear;
Rs = 40; % bandstop attenuation in dB
OmegaP1_1=500; % bandpass edge frequency
OmegaP1_2=700;% bandpass edge frequency
OmegaS1_1=400; % bandstop edge frequency
OmegaS1_2=800; %bandstop edge frequency
Ft=2000; % samling frequency
Wn=2/Ft*[OmegaP1_1 OmegaP1_2];% change analogy frequency to digital angular frequency
N = 23;num=fir1(N,Wn,hanning(N+1));%海明
w = 0:pi/255:pi;
h = freqz(num,1,w);
g = 20*log10(abs(h));
% 幅频绘制
subplot(2,1,1);
plot(w/pi,abs(h));grid
axis([0 1 0 1.3]);
title('Magnitude Spectrum |H(e^{j\omega})|');
xlabel('\omega /\pi');
ylabel('Amplitude');
% 增益绘制
subplot(2,1,2);
plot(w/pi,g);grid
axis([0 1 -60 5]);
xlabel('\omega /\pi'); ylabel('Gain in dB');
title('Gain Response of a FIR Bandpass Filter');