408-数据结构-树（二）

本文是 “408数据结构” 的复习笔记中“树”的部分，主要依据王道的课本，考408的小伙伴可以拿走原笔记。

有错误的地方还请各位留言指出，谢谢啦(ง •_•)ง

按照王道数据结构的章节目录，本篇文章有以下【一】个章节

• 树

相关术语

记根节点为 R

• 前驱节点和后继节点：分别表示父节点和子节点
• 层数：根节点为第一层，层次往下递增
• 树的高度：树中结点的最大层数，树能够到的最底层
• 结点的高度：从叶节点开始向上逐层累加
• 结点的深度：从根节点开始向下逐层累加
• 祖先结点：对于一个结点K，从K到R路径上的任意结点称为K的祖先结点
• 结点的度：一个结点的子节点个数称为该结点的度，树中结点的最大度称为树的度
• 结点间的路径长度：两个结点路径上边的个数【路径是从上向下的，只有直系长辈和晚辈之间才有路径，兄弟节点是不存在路径的】
• 结点路径长度：结点到根节点的路径长度
• 森林：把一颗树的根节点拿掉，就变成了多棵树（森林）

二叉树

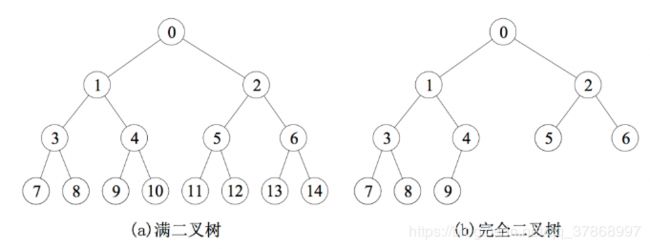
• 满二叉树

• 完全二叉树

所有叶结点都位于同一层的完全二叉树就是满二叉树

• 二叉排序树：左子树所有结点关键字＜根结点关键字＜右子树所有结点关键字
• 平衡二叉树：任一结点的左子树和右子树的深度之差不超过1

存储结构

顺序存储：数组，每一层最多有 1 2 4 8 个元素

链式存储：称为二叉链表

遍历

先序遍历

// recursive
void PreOrder(BiTree T){
    if(T != null){
        visit(T);           // 访问根节点
        PreOrder(T->left);	// 遍历左子树
        PreOrder(T->right); // 遍历右子树
    }
}

中序遍历

// recursive
void InOrder(BiTree T){
    if(T != null){
        InOrder(T->left);	// 遍历左子树
        visit(T);           // 访问根节点
        InOrder(T->right);  // 遍历右子树
    }
}

// non-recursive
// 非递归算法需要借助一个辅助栈，记为 S

// 算法的思想
/*
	中序遍历是先遍历左子树，再访问（输出）根节点，再遍历右子树
	所以处理一个结点时，必定先检查它有没有左子树
		如果有左子树
			就先不处理这个结点（压栈保存）
			转而处理它的左子结点
		如果没有左子树
			就可以访问这个结点（出栈输出）
			然后再处理它的右子节点
	栈里面的结点都正在等待处理自己的左子树
	换句话说
		只要栈里有结点，那么正在处理的结点必定是栈顶的结点左子树上的结点
		栈空的时候，即正在访问的结点V的左子树已处理完毕，接下来要去处理V的右子节点
	所以
		当栈空 并且 这个V的右子节点也没了（为空），整棵树处理完毕
*/

// 思考：结点进栈的顺序就是前序顺序，出栈的结点排序就得到了中序序列 (○´･д･)ﾉ

void InOrder2(BiTree T){
    InitStack(S);
    BiTree p = T;
    
    while(p || !IsEmpty(S)){	// 栈不空：还有遇到过但暂时放一边没处理的点；p不空：还有没遇到的结点
        if(p){
            Push(S,p);			// 根结点进栈
            p = p->left;		// 处理左子树
        }
        else{
            Pop(S,p);			// 栈顶结点左子树处理完毕，弹出栈顶
            visit(p);			// 访问栈顶结点（根结点）
            p = p->right;		// 处理右子树
        }
    }
}

后序遍历

// recursive
void PostOrder(BiTree T){
    if(T != null){
        PostOrder(T->left);		// 遍历左子树
        PostOrder(T->right);  	// 遍历右子树
        visit(T);           	// 访问根节点
    }
}

层遍历

// 需要借助一个队列，记为 Q
void LevelOrder(BiTree T){
    InitQueue(Q);
    BiTree p;
    EnQueue(Q,T);
    while(!IsEmpty(Q)){
        DeQueue(Q,p);			// 队头出队，队头是队内这些结点中，原来在树里最上层最左边的结点
        visit(p);
        if(p->left)
            EnQueue(Q,p->left)	// 左子节点入队
        if(p->right)
            EnQueue(Q,p->right)	// 右子节点入队
    }
}

能还原出二叉树结构的序列：

• 先序序列 + 中序序列：先序序列的第一个结点将中序序列分成左右子树（子序列），如此递归下去即可
• 后序序列 + 中序序列
• 层序序列 + 中序序列

不能还原成二叉树结构的序列：

• 后序序列 + 先序序列：不能确定唯一一棵二叉树，但可以确定结点的祖先关系。
  • 比如 前序序列为 a，[……]，后序序列为 [……]，a；则可以确定 a 为 [……] 内所有结点的祖先。递归地分析 [……] 内的串，最终也能得到一些信息

【2017-先序和中序】一棵非空二叉树的先序和中序序列相同，则其所有的非叶结点需要满足的条件是____

看看先序和中序的递归算法表示，只要 p->left 为空，它们就是一样的代码。所以答案填：

左子树为空（或者：只有右子树）

【2015-先序序列的本质】先序序列为 $a,b,c,d$ 的不同二叉树的个数是____

仔细研究一下中序遍历非递归写法中用到的的栈，一个前序顺序入栈，一个中序顺序出栈，就能唯一确定一颗二叉树。所以等价于 “已知入栈顺序为 $a,b,c,d$ ，则出栈顺序有多少种？”

对于 $n$ 个不同元素进栈，出栈序列的个数为 $\frac{1}{n+1}{C}_{2n}^n$ 种 相当精彩的推导过程

$n=4$ 带入得 14 种

【一些思考】

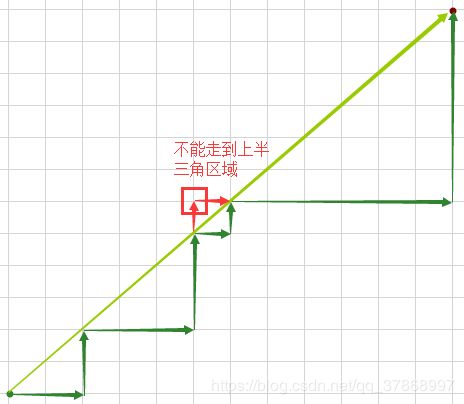
Q1：一个 $n\times n$ 的棋盘，一只崽在左下角，想走到右上角。可以向右，向上两个方向移动，但不能走到棋盘的上三角区，斜线上的点和下三角区域都能走，问有几种走法（不同的路径）

Q2：已知 $n$ 个不同元素的进栈顺序，有几种可能的出栈序列？

Q3：将 $n$ 个不同元素组成的序列视为二叉树的先序序列，能推导出多少棵不同的二叉树？

分析：

Q1、Q2、Q3 三问其实是等价的

• Q1本质上限制了横着走的格数≥竖着走的格数
• Q2中进栈出栈必然是有进栈的次数≥出栈的次数
• Q3中一个先序和一和中序唯一对应一棵二叉树，所以等价于已知先序序列能有多少中序序列，进一步分析中序遍历的非递归算法本质上就是先序进栈中序出栈，所以又回到了已知进栈序列求出栈序列种数的问题 = Q2

解决这些问题第一想法往往是递归回溯之类的，但其实这有通项公式，直接在 $O(1)$ 时间内解决不香吗

线索二叉树

一个有 n 个结点的二叉树，有 n+1 个空指针【$2n-(n-1)$，n-1 是因为根节点上头没有对应的边】

Q1：如何利用这些空指针？

一棵普通的链式二叉树，要获取某种遍历序列需要执行各种复杂遍历算法

Q2：有没有办法能直接找到一个结点在某种遍历序列中的前驱和后继？

Q1和Q2相互解决后的产物：线索二叉树（Threaded_tree）

线索二叉树的结点结构：

typedef struct ThreadNode{
    Type data;
    struct ThreadNode *LChild, *RChild;
    int LTag, RTag;
} ThreadNode, *ThreadTree;

LChild：两种含义，既可以指向左子结点，也可以指向结点前驱。

Ltag：用来区分LChild的两种含义，1：前驱；0：左子结点。

线索化：

将普通二叉树变成某种遍历序列的过程。

构造线索二叉树时不破坏原有的指向左右子结点的指针，只将空指针指向该遍历序列的前驱或者后继结点，并设置对应的 tag。

线索化后的二叉树又称为线索链表，线索化后得到的序列有头部和尾部，即头部的 LChild 为 null，尾部的 RChild 为 null。

// 中序线索化

void CreateInThread(ThreadTree T){
    ThreadTree pre = null;
    if(T != null){
        InThread(T, pre);		// 线索序列的第一个结点的前驱结点 pre 为 null
        						// 从 null 开始线索化 T
        
        pre->RChild = null;		// 线索序列的最后一个结点的后继结点 pre->RChild 为 null
        pre->RTag = 1;
    }
}


void InThread(ThreadTree &p, ThreadTree &pre){
    if(p != null){
        InThread(p->LChild, pre);	// 线索化左子树
        
        // ---
        if(p->LChild == null){		// 当前结点没有左孩子
            p->LChild = pre;		// 设置当前结点的的 LChild 为前驱结点 pre
            p->LTag = 1;			// 设置当前结点 p 的 LTag
        }
        
        if(pre != null && pre->RChild == null){	// 前驱节点没有右孩子
            pre->RChild = p;					// 设置前驱结点的后继结点 RChild 为当前节点 p
            pre->RTag = 1;						// 设置前驱结点的 RTag
        }
        // ---
        
        pre = p;
        InThread(p->RChild, pre);
    }
}

线索二叉树长这样

线索二叉树的操作：

线索二叉树能提供一些方便访问结点的方法

// 以中序线索二叉树（中序序列）为例

/* 找到第一个结点 */
ThreadNode *FirstNode(ThreadNode *p){
    while(p->LTag == 0)
        p = p->LChild;		// 左下就完事儿了
    return p;
}

/* 找到最后一个结点 */
ThreadNode *LastNode(ThreadNode *p){
    while(p->RTag == 0)
        p = p->RChild;		// 右下就完事儿了
    return p;
}

/* 找任意结点 p 的后继结点 */
ThreadNode *NextNode(ThreadNode *p){
    while(p->RTag == 0)
        return FirstNode(p->RChild);	// 有右孩子的话后继结点必是右子树的第一个结点
    return p->RChild;					// 直接看线索
}

/* 找任意结点 p 的前驱结点 */
ThreadNode *NextNode(ThreadNode *p){
    while(p->LTag == 0)
        return LastNode(p->LChild);		// 有左孩子的话前驱结点必是左子树的最后一个结点
    return p->LChild;					// 直接看线索
}

/* 中序遍历 */
void InOrder(ThreadNode *root){
    ThreadNode *p = FirstNode(root);	// 找到第一个
    while(p){
        visit(p);
        p = NextNode(p);				// 下一个（遍历起来真的很舒服 o(*￣▽￣*)ブ
    }
}

相关博客

树、森林

存储结构

三种常用结构：

• 双亲表示法：数组存储，每个元素（结点）有 data 和 parent 两个属性，parent 指出该结点的双亲结点所在的数组下标，其中，根节点 parent 值为 -1，表示没有

• 孩子表示法：每个节点的值用数组存起来，每个节点的孩子节点的下标用链表存起来

  typedef struct CNode{
      Type data;			// 节点数据
      IndexNode* childs;  // 孩子下标链表
  } CNode;
  
  typedef struct IndexNode{
      int index;			// 在数组中的下标
      IndexNode* next;	// 下一个孩子下标结点
  } IndexNode;
  
  #define MaxSize = 50
  typedef struct CTree{
      CNode tree[MaxSize];// 数组
  } CTree;
  

• 孩子双亲表示法：又称 “二叉树表示法”，结点包含三部分：data；指向第一个子结点的指针，指向下一个兄弟结点的指针

  typedef struct CSNode{
      ElemType data;
      struct CSNode *FirstChild, *NextBrother;
  } CSNode, *CSTree;
  

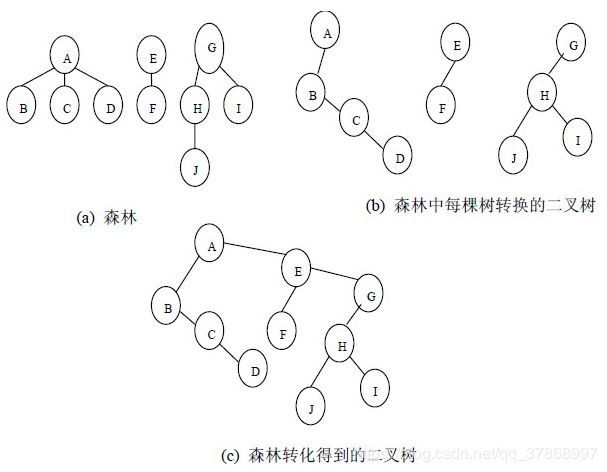
转换关系

参考博客

树 与 二叉树：孩子双亲表示法的规则

森林 与 二叉树：

遍历

树的遍历主要有两种：

• 先根遍历：先访问根节点，再从左到右遍历每棵子树
• 后根遍历：先从左到右遍历每棵子树，最后再访问根节点

森林的遍历两种

• 先序遍历：
  • 访问第一课树的根节点
  • 先序遍历第一棵树中根节点的子树森林
  • 先序遍历除第一颗树外剩下的树构成的森林
• 中序遍历
  • 中序遍历第一棵树中根节点的子树森林
  • 访问第一课树的根节点
  • 中序遍历除第一颗树外剩下的树构成的森林

遍历序列的对应关系

树	森林	二叉树
先根遍历	先序遍历	先序遍历
后根遍历	中序遍历	中序遍历

并查集（Union-Find）

采用双亲表示法，全集（森林）由若干个小集合（树）组成

有意思；interesting；

一个全集合为 $S=\{0,1,2,3,4,5,6,7,8,9\}$，初始化时每个元素作为一个独立集合，不与其它元素有联系

一个元素 A 的 data：

• +a 时：A 的双亲结点是 a 号元素
• -a 时：A 是一个集合的代表（树的根节点），这个集合（树）一共有 a 个结点

初始化 $S$ 时，数组如下

元素	0	1	2	3	4	5	6	7	8	9
data	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1

操作后，$S$ 内部分成了 3 个连通区（三棵树）$S_1=\{0,6,7,8\}$，$S_2=\{1,4,9\}$，$S_3\{2,3,5\}$，数组如下

元素	0	1	2	3	4	5	6	7	8	9
data	-4	-3	-3	2	1	2	0	0	0	1

每个区域有一个代表（树的根节点）

在 $S_1$ 和 $S_2$ 两区域之间修一条路把两区域连起来，即取并集（$S_1\cup S_2$）

元素	0	1	2	3	4	5	6	7	8	9
data	-4	0	-3	2	1	2	0	0	0	1

将 $S_2$ 的根节点变成 $S_1$ 根节点的小弟

二叉排序树（BST）

basic-rule：左子树所有结点关键字＜根结点关键字＜右子树所有结点关键字

中序遍历二叉排序树可以得到关键字的递增序列

构造，查找，插入，删除这些操作只要维护这个 base-rule 即可

根据输入数据的顺序不同，构造出二叉排序树的结构也会不同，树的结构（高度）直接影响了排序树的查找效率

二叉排序树的查找与有序数组的二分查找的分析与对比

• 单纯的二叉排序树的平均查找效率取决于树的高度 $O(h)$ ，数据增删效率高
• 有序数组（顺序存储）的二分查找性能稳定为 $O(lo{g}_{2}n)$ ，但不适合数据的增删

所以，当有序表是静态查找表时，宜用顺序表存储二分查找；若有序表是动态查找表时，宜用二叉排序树

为了让二叉排序树性能稳定，除了要维护 basic-rule 之外，还要维护树的结构，升级为下面这个靓仔

平衡二叉树（AVL）

每一个结点添加一个参数：平衡因子 = 左子树的高度 - 右子树的高度

维护树结构的方式是将平衡因子限制在 { -1，0，1 } 三个值（合理范围）内

构造，插入，删除这些操作的过程中，一旦某些结点的平衡因子超过了合理范围，就调整最小不平衡子树的结构，纠正平衡因子。【调整结构不能破坏 basic-rule】

如何调整？——四种旋转

每种旋转得到的都是究极平衡的树

此处有很 nice 的交互

• RR — 左单旋转：二五仔在结点A的右孩子（R）的右子树（R）上
  

• LL — 右单旋转：二五仔在结点A的左孩子（L）的左子树（L）上
  

• LR — 先左后右：在结点A的左孩子（L）的右子树（R）上多一个二五仔【下图删除结点 30】

• RL — 先右后左：在结点A的右孩子（R）的左子树（L）上多出二五仔【下图插入结点 18】

【2012-AVL树平衡因子】若平衡二叉树的高度为 6，所有非叶子结点的平衡因子均为 1，则该平衡二叉树的结点总数为____

记 $C_n$ 是高度为 $n$ 的平衡二叉树的结点总数，平衡因子为 1 得左子树结点数为 $C_{n-1}$ ，右子树结点总数为 $C_{n-2}$ ，可得递推公式： $C_n=C_{n-1}+C_{n-2}+1$ ，动手画画可得$C_1=1,C_2=2$；

$n=6$ 带入得 20

【2013-AVL树的构造】将关键字 $1,2,3,4,5,6,7$ 依次插入初始为空的AVL树，最后树长什么样？

try yourself

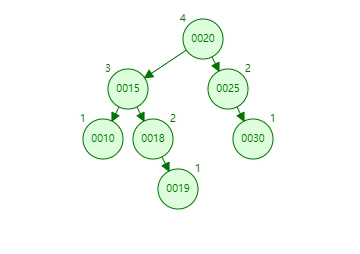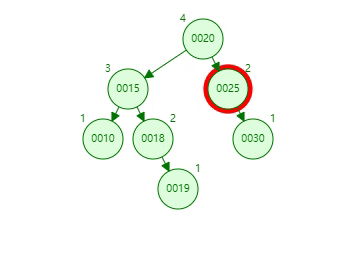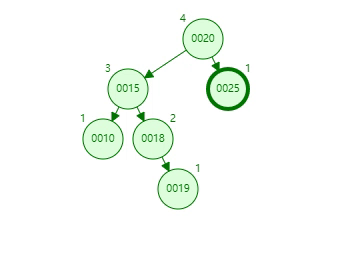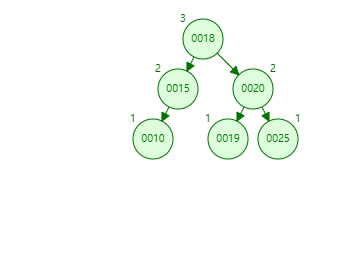
【思考】AVL树长下面这样，现在删了 4 号男嘉宾，树会怎么变

删除一个父节点后，会先把这个节点左子树上的最大值移动过去（维护 basic-rule）

再维护平衡结构，最终结果如下

哈夫曼树（Huffman）

背景概念：

• 结点被赋予一个表示某种意义的权值，称为权
• 从根节点到任意结点的路径长度（经过的边数） × 这个节点的权 = 这个结点的带权路径长度（WPL）
• 树中所有叶节点的带权路径长度之和为这棵树的带权路径长度

概念：

有一堆带权的结点，显然用这些点可以构造很多棵不同的树，而这些树中带权路径长度最小的那棵就是最靓的仔，江湖人称哈夫曼树，也叫最优二叉树。

将这堆结点构造成哈夫曼树的算法

自底向上的思想，将权值最低的放在最下面

1. 给出的 $n$ 个结点记为 $F$
2. 从 $F$ 中移除两个权值最小的节点，将它们的权值相加，形成一个新节点加到 $F$；（这个新结点就是两个权值最小的结点的双亲结点）
3. 重复 1，2 过程直到剩下最后一个结点，这就是根节点，这个根节点的权值就是哈夫曼树的带权路径长度

琢磨一下这个过程，发现哈夫曼树中没有度为 1 的结点，即父节点的权值不可能等于其子结点权值

应用：对每个字符使用固定长度的二进制串去编码的方式叫 固定长度编码，但由于字符出现的频率不同，有高频率有低频率，我们希望对高频率的字符用比低频的字符更短的编码长度，从而达到数据压缩的效果

这种变长编码方式称为哈夫曼编码，因为它能由哈夫曼树很自然地得到（字符频率为结点权值，0，1为结点左右子结点的边，叶子节点为字母，则从根结点到叶子结点的路径就是叶子节点字母对应的二进制串，）

前缀编码：任何一个字母的编码都不是另一个字母编码的前缀（能构造哈夫曼树，所有字符都在叶结点上）

下图对 ‘u’, ‘r’, ‘i’, ‘e’, ‘l’, ‘w’, ’ '（空格）七个字符的哈夫曼编码树参考博客

数据压缩率：

比如有 $a,b,c,d,e,f$ 六个字母，每个字母用 3 bits 来表示，一篇一百字母的文章需要 300 bits，

现统计文章中字母的频率分别为 45，13，12，16，9，5，构造哈夫曼树并计算WPL为 224 bits

则哈夫曼编码使得文章从 300 bits 压缩到 224 bits

【2012-多个有序列表合并】设有 6 个升序列表 A、B、C、D、E、F，分别含有 10、35、40、50、60、200个数据，要求通过 5 次两两合并，最终得到 1 个升序列表。设计一个最坏情况下比较次数最少的算法。

题目已经限制了合并操作为两两合并，所以不用考虑其它算法，像题目问的一样思考如何让比较次数最少。由于最先合并的表中元素在之后的每次合并都会被比较，所以要让元素少的序列最先合并，这种想法与哈夫曼树的思想不谋而合，构建一棵以元素数量为权重的哈夫曼树，让树的WPL最小即可

【思考】自己思考一下合并多个升序序列的算法。

给出一种思路：假设有 $m$ 个序列，它们一共有 $n$ 个数，下方给出的是一个时间复杂度 $O(nlo{g}_{2}m)$ 的算法。

维护一个含有 $m$ 个结点的最小堆，是的，这 $m$ 个结点指向 $m$ 个序列的第一个元素。每次取出堆顶数（所有序列中最小的），接着堆顶结点自然指向堆顶序列的下一个数，然后重新维护这个堆。如此往复，每取一个数，花费 $O(lo{g}_{2}m)$ 时间去维护堆结构，然后一共取 $n$ 次堆顶（n个数）。

其它相关文章

• 408-数据结构-线性表、栈、队列（一）
• 408-数据结构-图（三）
• 408-数据结构-查找、排序（四）